2.1.2 椭圆的简单几何性质 课件3
文档属性
| 名称 | 2.1.2 椭圆的简单几何性质 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览










文档简介
课件43张PPT。圆锥曲线与方程第二章2.1 椭圆
椭圆的简单几何性质第二章1.理解椭圆的简单几何性质.
2.利用椭圆的简单几何性质解决一些简单问题.重点:利用椭圆的标准方程研究椭圆的几何性质.
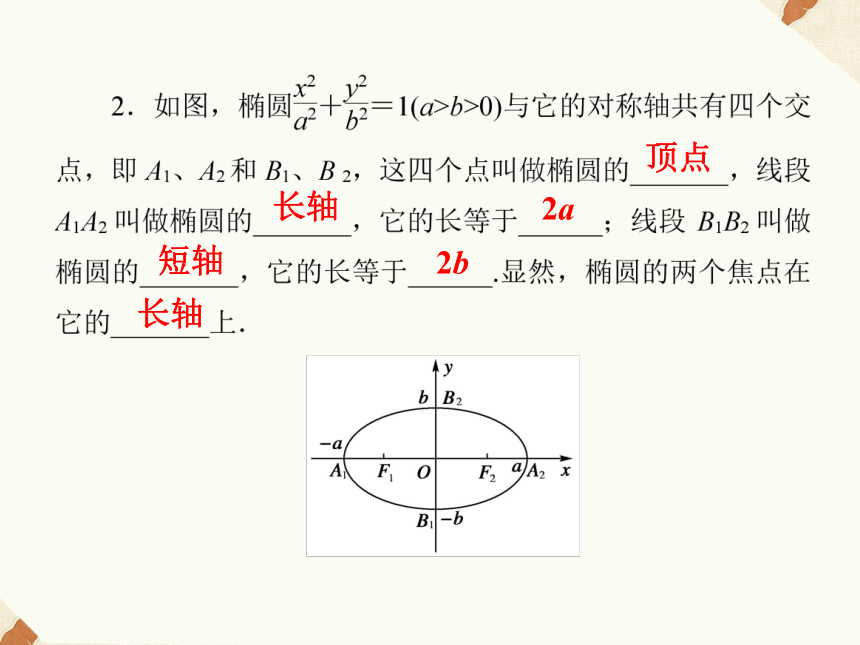
难点:椭圆的几何性质的实际应用.椭圆的简单几何性质思维导航 中心 轴-x-yxyx轴y轴坐标原点中心顶点长轴2a短轴2b长轴思维导航
2.观察不同的椭圆可见它们的扁平程度不一样,哪些量影响其扁平程度?怎样刻画?
新知导学
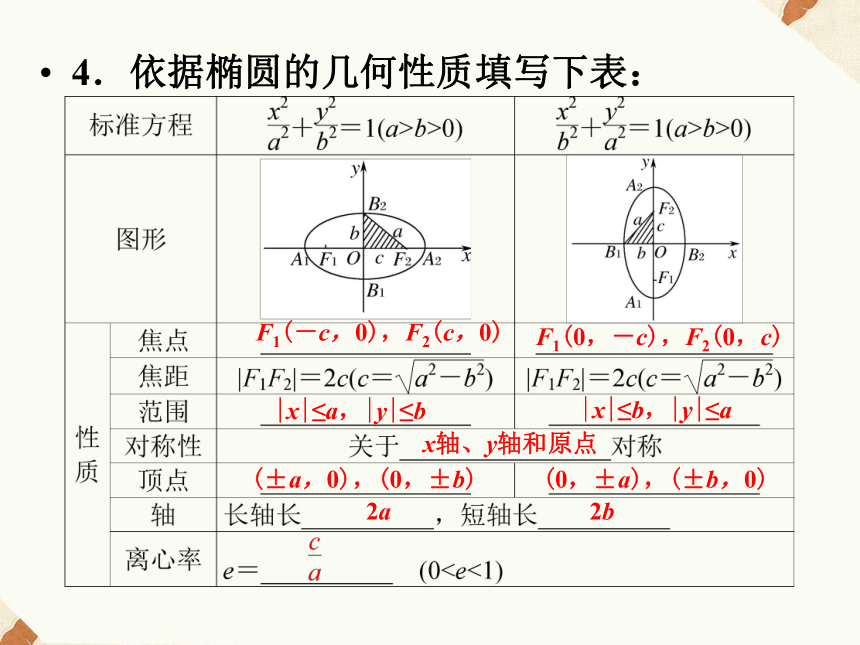
3.椭圆的焦距与长轴长的比叫做椭圆的__________.离心率4.依据椭圆的几何性质填写下表:F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)|x|≤a,|y|≤b|x|≤b,|y|≤ax轴、y轴和原点(±a,0),(0,±b)(0,±a),(±b,0)2a2b6.根据曲线的方程,研究曲线的几何性质,并正确地画出它的图形,是解析几何的基本问题之一.本节就是根据椭圆的标准方程来研究它的几何性质.其性质可分为两类:一类是与坐标系无关的本身固有性质,如____________、______、__________;一类是与坐标系有关的性质,如__________、__________.长、短轴长焦距离心率顶点焦点[答案] D[答案] C4.求椭圆9x2+y2=81的长轴长、短轴长、焦点坐标、顶点坐标和离心率.[分析] 由题目可获取以下主要信息:①已知椭圆的方程;②研究椭圆的几何性质.解答本题可先把方程化成标准形式然后再写出性质.椭圆的主要几何量
[方法规律总结] 由椭圆方程讨论其几何性质的步骤:
(1)化椭圆方程为标准形式,确定焦点在哪个轴上.
(2)由标准形式求a、b、c,写出其几何性质.求椭圆25x2+16y2=400的长轴长、短轴长、离心率、焦点坐标和顶点坐标.利用椭圆的几何性质求标准方程
[方法规律总结] 已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:(1)确定焦点所在的位置,以确定椭圆方程的形式;(2)确立关于a、b、c的方程(组),求出参数a、b、c;(3)写出标准方程.求椭圆的离心率 [解析] 如图,连接BF2.
(3)若已知b、c,则求a,再利用(1)或(2)求解;
(4)若已知a、b、c的关系,可转化为关于离心率e的方程(不等式)求值(范围).
(5)给出图形的问题,先由图形和条件找到a、b、c的关系,再列方程(不等式)求解.[答案] B[解题思路探究] 第一步,审题:审结论明确解题方向,求m的取值范围,需利用条件建立关于m的不等式求解;审条件,发掘解题信息,直线与椭圆有公共点,则联立方程组有解,焦点在x轴上,则x2项的分母较大.
第二步,建联系,找解题突破口,确定解答步骤.由直线过定点,若定点在椭圆上或椭圆内,则直线与椭圆有公共点;将直线与椭圆方程联立消元,当Δ≥0时,直线与椭圆有公共点.
第三步,规范解答.[辨析] 上述解法没有讨论焦点的位置,而默认了椭圆的焦点在x轴上.
椭圆的简单几何性质第二章1.理解椭圆的简单几何性质.
2.利用椭圆的简单几何性质解决一些简单问题.重点:利用椭圆的标准方程研究椭圆的几何性质.
难点:椭圆的几何性质的实际应用.椭圆的简单几何性质思维导航 中心 轴-x-yxyx轴y轴坐标原点中心顶点长轴2a短轴2b长轴思维导航
2.观察不同的椭圆可见它们的扁平程度不一样,哪些量影响其扁平程度?怎样刻画?
新知导学
3.椭圆的焦距与长轴长的比叫做椭圆的__________.离心率4.依据椭圆的几何性质填写下表:F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)|x|≤a,|y|≤b|x|≤b,|y|≤ax轴、y轴和原点(±a,0),(0,±b)(0,±a),(±b,0)2a2b6.根据曲线的方程,研究曲线的几何性质,并正确地画出它的图形,是解析几何的基本问题之一.本节就是根据椭圆的标准方程来研究它的几何性质.其性质可分为两类:一类是与坐标系无关的本身固有性质,如____________、______、__________;一类是与坐标系有关的性质,如__________、__________.长、短轴长焦距离心率顶点焦点[答案] D[答案] C4.求椭圆9x2+y2=81的长轴长、短轴长、焦点坐标、顶点坐标和离心率.[分析] 由题目可获取以下主要信息:①已知椭圆的方程;②研究椭圆的几何性质.解答本题可先把方程化成标准形式然后再写出性质.椭圆的主要几何量
[方法规律总结] 由椭圆方程讨论其几何性质的步骤:
(1)化椭圆方程为标准形式,确定焦点在哪个轴上.
(2)由标准形式求a、b、c,写出其几何性质.求椭圆25x2+16y2=400的长轴长、短轴长、离心率、焦点坐标和顶点坐标.利用椭圆的几何性质求标准方程
[方法规律总结] 已知椭圆的几何性质,求其标准方程主要采用待定系数法,解题步骤为:(1)确定焦点所在的位置,以确定椭圆方程的形式;(2)确立关于a、b、c的方程(组),求出参数a、b、c;(3)写出标准方程.求椭圆的离心率 [解析] 如图,连接BF2.
(3)若已知b、c,则求a,再利用(1)或(2)求解;
(4)若已知a、b、c的关系,可转化为关于离心率e的方程(不等式)求值(范围).
(5)给出图形的问题,先由图形和条件找到a、b、c的关系,再列方程(不等式)求解.[答案] B[解题思路探究] 第一步,审题:审结论明确解题方向,求m的取值范围,需利用条件建立关于m的不等式求解;审条件,发掘解题信息,直线与椭圆有公共点,则联立方程组有解,焦点在x轴上,则x2项的分母较大.
第二步,建联系,找解题突破口,确定解答步骤.由直线过定点,若定点在椭圆上或椭圆内,则直线与椭圆有公共点;将直线与椭圆方程联立消元,当Δ≥0时,直线与椭圆有公共点.
第三步,规范解答.[辨析] 上述解法没有讨论焦点的位置,而默认了椭圆的焦点在x轴上.
