2.2.1 双曲线及其标准方程 课件1
文档属性
| 名称 | 2.2.1 双曲线及其标准方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 239.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览


文档简介
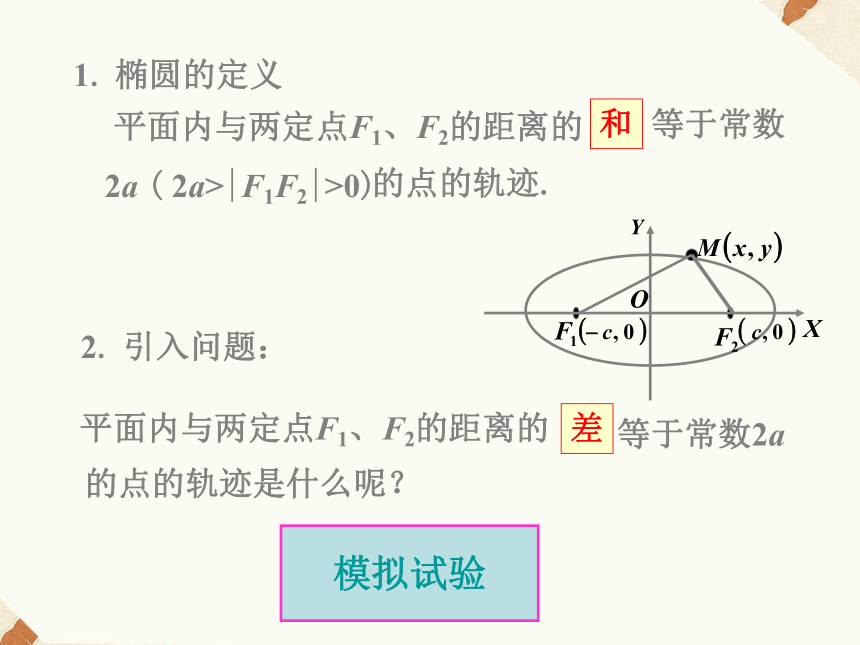
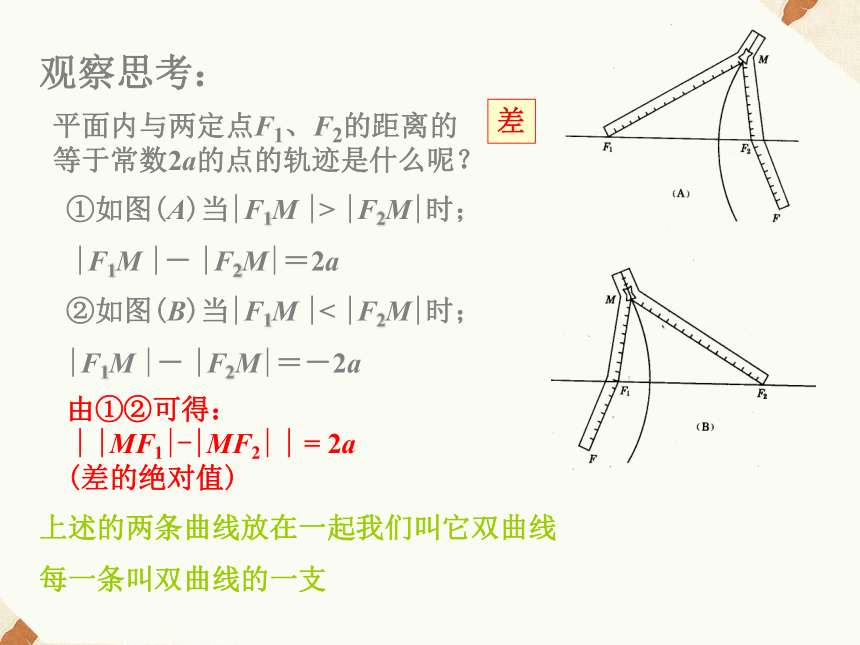
课件11张PPT。2.2.1双曲线及其标准方程1. 椭圆的定义模拟试验观察思考:②如图(B)当|F1M |< |F2M|时;
|F1M |- |F2M|=-2a ①如图(A)当|F1M |> |F2M|时;
|F1M |- |F2M|=2a差平面内与两定点F1、F2的距离的 等于常数2a的点的轨迹是什么呢?上述的两条曲线放在一起我们叫它双曲线
每一条叫双曲线的一支 由①②可得:
| |MF1|-|MF2| | = 2a
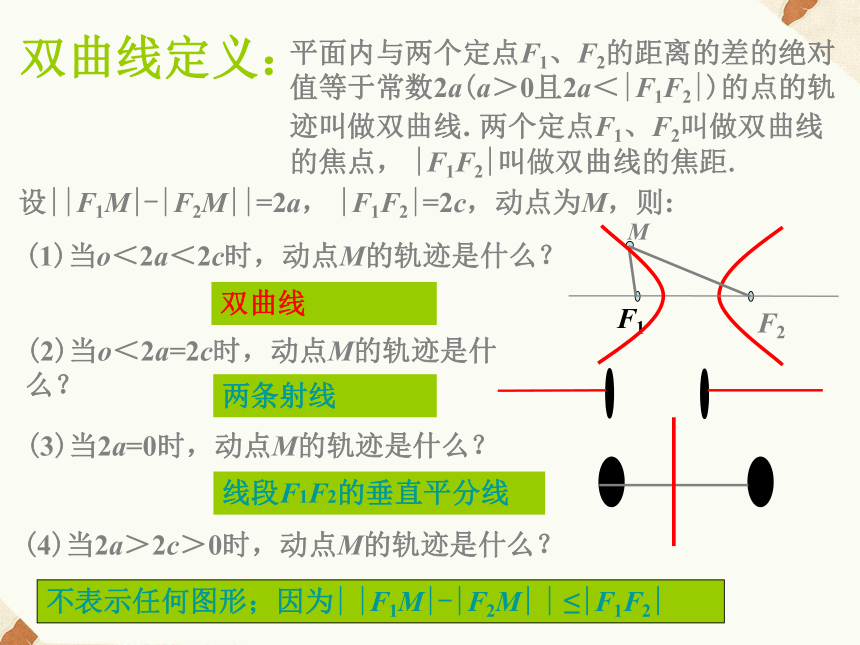
(差的绝对值)双曲线定义:平面内与两个定点F1、F2的距离的差的绝对值等于常数2a(a>0且2a<|F1F2|)的点的轨迹叫做双曲线.两个定点F1、F2叫做双曲线的焦点, |F1F2|叫做双曲线的焦距.设||F1M|-|F2M||=2a, |F1F2|=2c,动点为M,则:双曲线两条射线线段F1F2的垂直平分线 双曲线标准方程推导:(1)建系设标;M(x,y)以过点F1、F2的直线为x轴,线段F1F2的中垂线为y轴,建立直角坐标系;设M(x,y)是双曲线上任意一点,且F1F2=2c,则F1(-c,0)、F2(c,0).(2)写出点M的集合;(3)列出方程;(4)整理化简;(c2-a2)x2-b2y2=a2(c2-a2)令 c2-a2=b2双曲线标准方程:∵∴(1)焦点在x轴上(2)焦点在y轴上F1(-c, 0)、F2( c , 0)F1(0, -c)、F2( 0, c )特
征(1)方程的右边是1,方程的左边是平方差的形式;(2)双曲线的焦点所在的坐标轴与方程左边正项的分
子相对应.c2-a2=b2例1 已知双曲线两个焦点的坐标为F1(-5,0)F2(5,0),双曲线上一点P到F1 、F2的距离的差的绝对值等于6,求双曲线的标准方程.∵2a=6,2c=10, ∴a=3,c=5.∴b2=52-32=16.例3 求满足下列条件的双曲线标准方程:
(1)若a=6,b=3,焦点在x轴上;
(2)若a= ,过点A(2,-5),
焦点在y轴上;
(3)若a=6,c=10,焦点在坐标轴上.答案:(1)
(2)
(3)x236-y29=1x236-y264=1x220-y216=1x236-y264=1或{m|m>-1或m<-2}同为F( 4,0)若为双曲线,则(2+m)(m+1)>0,2、已知方程 表示双曲线,
则m的取值范围是________________;
3、方程 表示双曲线时,则m的取
值范围_________________.yc2=a2+b2小结:||MF1|—|MF2||=2a(2a<|F1F2|)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)
|F1M |- |F2M|=-2a ①如图(A)当|F1M |> |F2M|时;
|F1M |- |F2M|=2a差平面内与两定点F1、F2的距离的 等于常数2a的点的轨迹是什么呢?上述的两条曲线放在一起我们叫它双曲线
每一条叫双曲线的一支 由①②可得:
| |MF1|-|MF2| | = 2a
(差的绝对值)双曲线定义:平面内与两个定点F1、F2的距离的差的绝对值等于常数2a(a>0且2a<|F1F2|)的点的轨迹叫做双曲线.两个定点F1、F2叫做双曲线的焦点, |F1F2|叫做双曲线的焦距.设||F1M|-|F2M||=2a, |F1F2|=2c,动点为M,则:双曲线两条射线线段F1F2的垂直平分线 双曲线标准方程推导:(1)建系设标;M(x,y)以过点F1、F2的直线为x轴,线段F1F2的中垂线为y轴,建立直角坐标系;设M(x,y)是双曲线上任意一点,且F1F2=2c,则F1(-c,0)、F2(c,0).(2)写出点M的集合;(3)列出方程;(4)整理化简;(c2-a2)x2-b2y2=a2(c2-a2)令 c2-a2=b2双曲线标准方程:∵∴(1)焦点在x轴上(2)焦点在y轴上F1(-c, 0)、F2( c , 0)F1(0, -c)、F2( 0, c )特
征(1)方程的右边是1,方程的左边是平方差的形式;(2)双曲线的焦点所在的坐标轴与方程左边正项的分
子相对应.c2-a2=b2例1 已知双曲线两个焦点的坐标为F1(-5,0)F2(5,0),双曲线上一点P到F1 、F2的距离的差的绝对值等于6,求双曲线的标准方程.∵2a=6,2c=10, ∴a=3,c=5.∴b2=52-32=16.例3 求满足下列条件的双曲线标准方程:
(1)若a=6,b=3,焦点在x轴上;
(2)若a= ,过点A(2,-5),
焦点在y轴上;
(3)若a=6,c=10,焦点在坐标轴上.答案:(1)
(2)
(3)x236-y29=1x236-y264=1x220-y216=1x236-y264=1或{m|m>-1或m<-2}同为F( 4,0)若为双曲线,则(2+m)(m+1)>0,2、已知方程 表示双曲线,
则m的取值范围是________________;
3、方程 表示双曲线时,则m的取
值范围_________________.yc2=a2+b2小结:||MF1|—|MF2||=2a(2a<|F1F2|)F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)
