2.2.2 双曲线的简单几何性质 课件1
文档属性
| 名称 | 2.2.2 双曲线的简单几何性质 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 398.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览







文档简介
课件29张PPT。第二章
圆锥曲线与方程双曲线的简单几何性质2.2.2让我们一起研究:标准方程为:
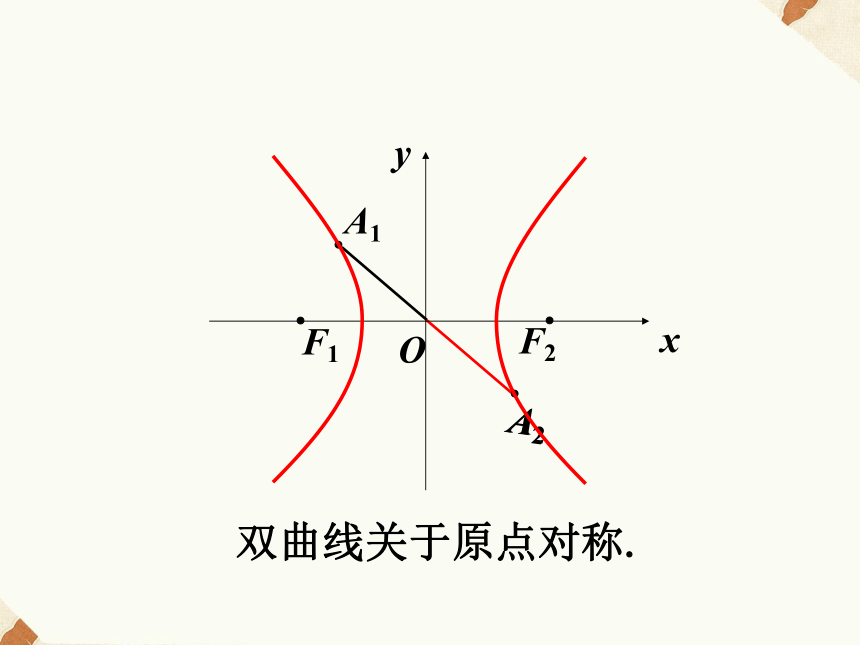
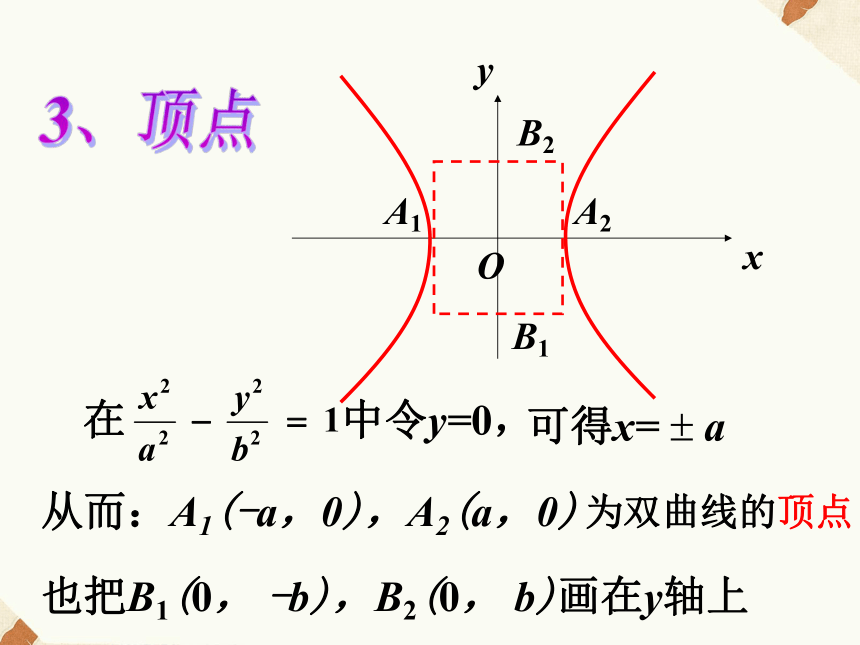
的双曲线的性质.F2F1OA1A2xy1、范围横坐标的范围:从而: x ? -a或 x ? a由式子 知 x ? -a或 x ? a所以 2、对称性F2F1Oxy双曲线关于y轴对称.F2F1Oxy双曲线关于x轴对称.A2A1F2F1Oxy双曲线关于原点对称.F2F1Oxy2、对称性双曲线关于y轴、x轴、原点对称.为什么?3、顶点OB2B1A1A2xy可得x= ? a从而:A1(-a,0),A2(a,0)也把B1(0, -b),B2(0, b)画在y轴上在 中令y=0,为双曲线的顶点3、顶点OB2B1A1A2xy线段A1A2叫双曲线的实轴;线段B1B2叫双曲线的虚轴.长为2a长为2b4、渐近线OB2B1A1A2xy红色虚框的两条对角线,为双曲线的
渐近线ab其方程为一般结论:双曲线 的渐近线为 练习1、计算下列双曲线的渐近线:你能发现什么规律吗?在方程 中,如果a=b,那么,
虚线方框是正方形,
并且实轴等于虚轴.OB2B1A1A2y实轴和虚轴等长的双曲线叫 等轴双曲线.5、离心率上面双曲线的形状有什么变化?怎样刻画它们的扁平程度?OA1A2y5、离心率双曲线的焦距与长轴长的比称为双曲线的离心率,用e表示,即OA1A2ye变大,双曲线的形状会怎样变化?关于x轴、y轴、原点对称(-a,0) , (a,0)(0,-a) , (0,a)例1、求双曲线 的实半轴长,
虚半轴长,焦点坐标,离心率.渐近线方程.解:把方程化为标准方程:可得:实半轴长a=4虚半轴长b=3半焦距c=焦点坐标是(0,-5),(0,5)离心率:渐近线方程:练习1、求下面双曲线的范围,顶点坐标,焦点坐标,实轴长,虚轴长,焦距,离心率,渐近线方程.
9x2-y2=81焦点坐标是顶点坐标是(-3,0) , (3,0) , (0,-9) , (0,9)实轴长2a=6,虚轴长2b=18,焦距2c=离心率e=渐近线方程:练习2:求适合下列条件的双曲线的
标准方程.
(1)实轴在x轴上,离心率e= ,b=2(3)过点(-1,3)和双曲线
有共同的渐近线. (2)过点(3,4)且虚轴长为实轴长的2倍(1)实轴在x轴上,离心率e= ,b=2(2)过点(3,4)且虚轴长为实轴长的2倍或(3)过点(-1,3)和双曲线
有共同的渐近线. 例2、双曲线型冷却塔的外形,是双曲线的
一部分绕其虚轴旋转所成的曲面,它的最
小半径为12m,上口半径为13m,下口半径
为25m,高为55m,试选择适当的坐标系,
求出此双曲线的方程(精确到1m).B12B'A'C'13AC25解:如图,建立直角坐
标系xoy,使小圆的
直径AA'在x轴上,
圆心与原点重合,设双曲线的方程为令C的坐标为(13,y), 则B的坐标为(25,y-55)将B、C坐标代入方程得B12B'A'C'13AC25由方程②,得(负值舍去)B12B'A'C'13AC25代入方程①得,化简得用计算器解得b≈25所以,
所求双曲线的方程为例3、点M(x,y)到定点F(5,0)的距离和它到
定直线l: 的距离的比是常数 ,求
点M的轨迹.解:设d是点M到直线l的距离,
根据题意,MFHdl所求轨迹就是集合MFHdl由此得将上式两边平方,并化简得9x2-16y2=144它是一条双曲线.即:小结
圆锥曲线与方程双曲线的简单几何性质2.2.2让我们一起研究:标准方程为:
的双曲线的性质.F2F1OA1A2xy1、范围横坐标的范围:从而: x ? -a或 x ? a由式子 知 x ? -a或 x ? a所以 2、对称性F2F1Oxy双曲线关于y轴对称.F2F1Oxy双曲线关于x轴对称.A2A1F2F1Oxy双曲线关于原点对称.F2F1Oxy2、对称性双曲线关于y轴、x轴、原点对称.为什么?3、顶点OB2B1A1A2xy可得x= ? a从而:A1(-a,0),A2(a,0)也把B1(0, -b),B2(0, b)画在y轴上在 中令y=0,为双曲线的顶点3、顶点OB2B1A1A2xy线段A1A2叫双曲线的实轴;线段B1B2叫双曲线的虚轴.长为2a长为2b4、渐近线OB2B1A1A2xy红色虚框的两条对角线,为双曲线的
渐近线ab其方程为一般结论:双曲线 的渐近线为 练习1、计算下列双曲线的渐近线:你能发现什么规律吗?在方程 中,如果a=b,那么,
虚线方框是正方形,
并且实轴等于虚轴.OB2B1A1A2y实轴和虚轴等长的双曲线叫 等轴双曲线.5、离心率上面双曲线的形状有什么变化?怎样刻画它们的扁平程度?OA1A2y5、离心率双曲线的焦距与长轴长的比称为双曲线的离心率,用e表示,即OA1A2ye变大,双曲线的形状会怎样变化?关于x轴、y轴、原点对称(-a,0) , (a,0)(0,-a) , (0,a)例1、求双曲线 的实半轴长,
虚半轴长,焦点坐标,离心率.渐近线方程.解:把方程化为标准方程:可得:实半轴长a=4虚半轴长b=3半焦距c=焦点坐标是(0,-5),(0,5)离心率:渐近线方程:练习1、求下面双曲线的范围,顶点坐标,焦点坐标,实轴长,虚轴长,焦距,离心率,渐近线方程.
9x2-y2=81焦点坐标是顶点坐标是(-3,0) , (3,0) , (0,-9) , (0,9)实轴长2a=6,虚轴长2b=18,焦距2c=离心率e=渐近线方程:练习2:求适合下列条件的双曲线的
标准方程.
(1)实轴在x轴上,离心率e= ,b=2(3)过点(-1,3)和双曲线
有共同的渐近线. (2)过点(3,4)且虚轴长为实轴长的2倍(1)实轴在x轴上,离心率e= ,b=2(2)过点(3,4)且虚轴长为实轴长的2倍或(3)过点(-1,3)和双曲线
有共同的渐近线. 例2、双曲线型冷却塔的外形,是双曲线的
一部分绕其虚轴旋转所成的曲面,它的最
小半径为12m,上口半径为13m,下口半径
为25m,高为55m,试选择适当的坐标系,
求出此双曲线的方程(精确到1m).B12B'A'C'13AC25解:如图,建立直角坐
标系xoy,使小圆的
直径AA'在x轴上,
圆心与原点重合,设双曲线的方程为令C的坐标为(13,y), 则B的坐标为(25,y-55)将B、C坐标代入方程得B12B'A'C'13AC25由方程②,得(负值舍去)B12B'A'C'13AC25代入方程①得,化简得用计算器解得b≈25所以,
所求双曲线的方程为例3、点M(x,y)到定点F(5,0)的距离和它到
定直线l: 的距离的比是常数 ,求
点M的轨迹.解:设d是点M到直线l的距离,
根据题意,MFHdl所求轨迹就是集合MFHdl由此得将上式两边平方,并化简得9x2-16y2=144它是一条双曲线.即:小结
