2.3.1 抛物线及其标准方程 课件1
文档属性
| 名称 | 2.3.1 抛物线及其标准方程 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 440.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 10:48:00 | ||
图片预览






文档简介
课件30张PPT。2.3.1
抛物线及其标准方程第2章 圆锥曲线与方程生活中的抛物线抛物线模型抛物线碟形天线抛物线灯一条抛物线.其顶点坐标是什么?对称轴是什么?我们怎么画一条抛物线呢?动画二次函数y=ax2+bx+c(a≠0)的图象是 平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线定点F叫做抛物线的焦点.定直线l叫做抛物线的准线. 抛物线的定义:如何建立适当的
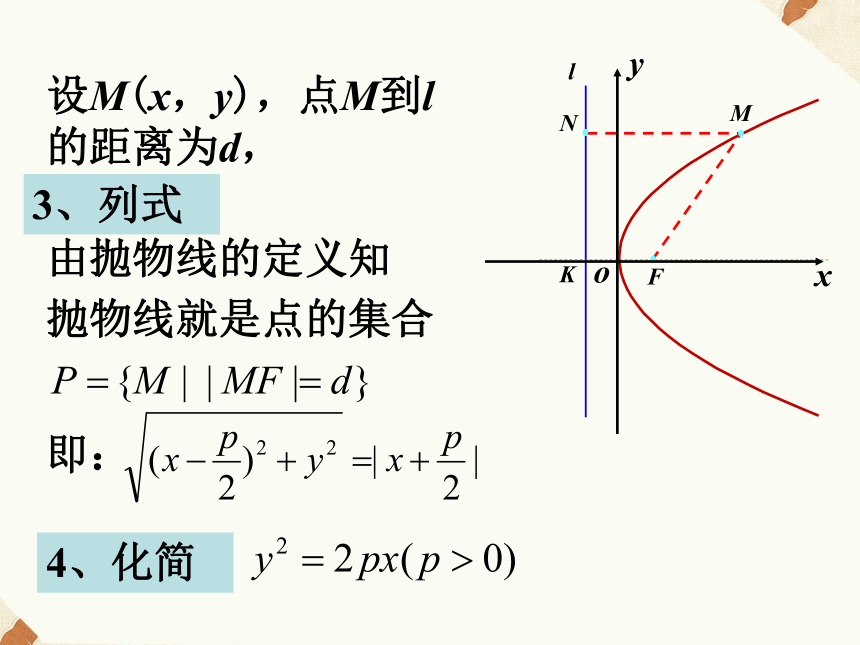
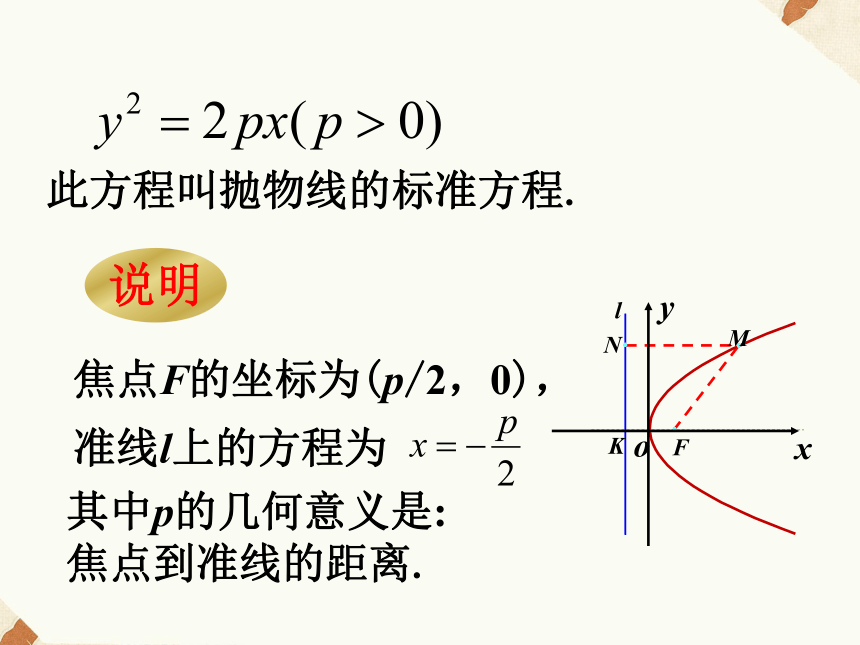
直角坐标系?那么焦点F的坐标为(p/2,0),lFKMNoyx标准方程的推导1、建系设F在直线l上的垂足为K,以FK的中点为坐标原点,以KF为x轴,建立直角坐标系.2、设点设|KF|=p(p>0),准线l上的方程为lFKMNoyx3、列式设M(x,y),点M到l的距离为d,由抛物线的定义知抛物线就是点的集合即:4、化简此方程叫抛物线的标准方程.焦点F的坐标为(p/2,0),准线l上的方程为其中p的几何意义是:
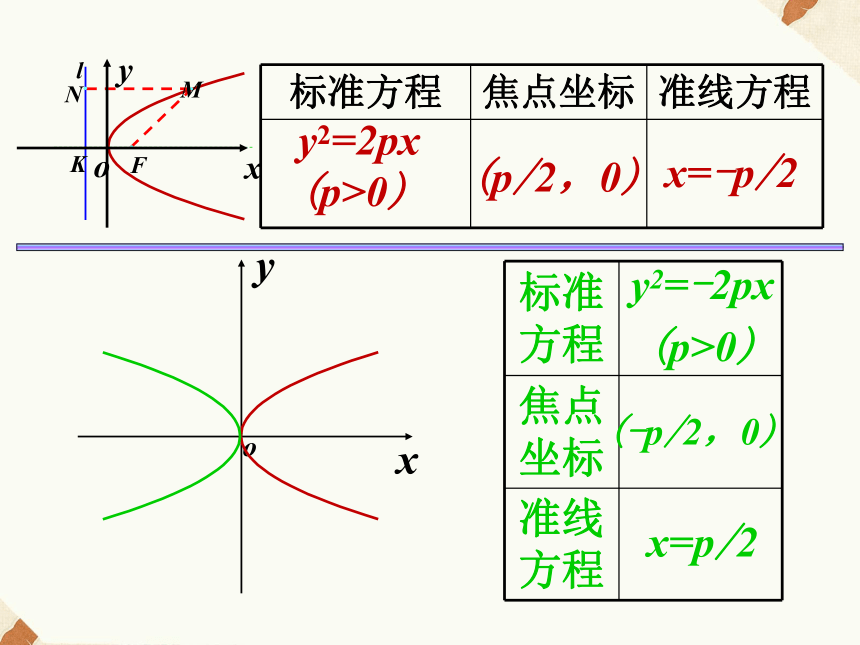
焦点到准线的距离.说明一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.xyoy2=-2px
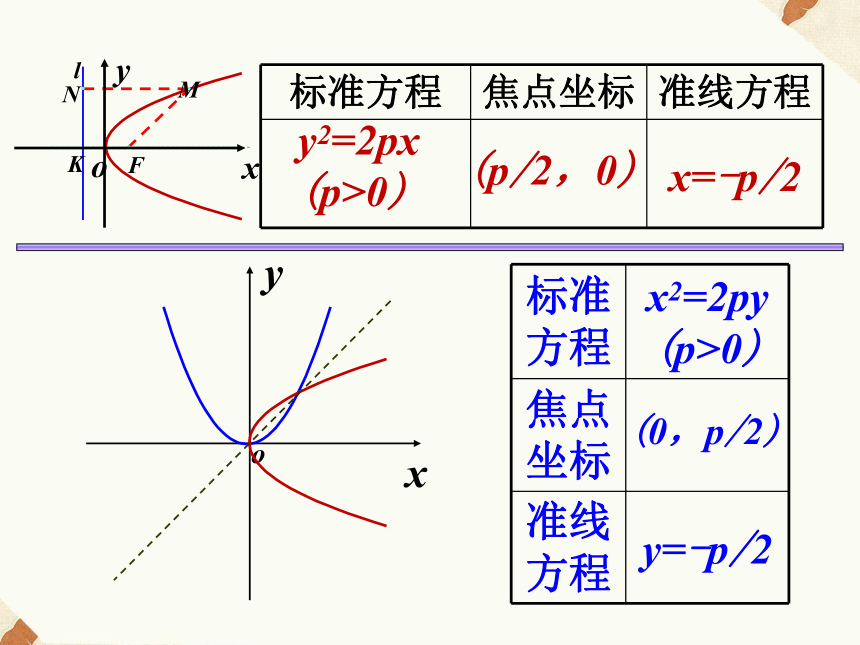
(p>0)(-p/2,0)x=p/2y2=2px (p>0)(p/2,0)x=-p/2xyox2=2py(p>0)(0,p/2)y=-p/2y2=2px (p>0)(p/2,0)x=-p/2xyox2=-2py
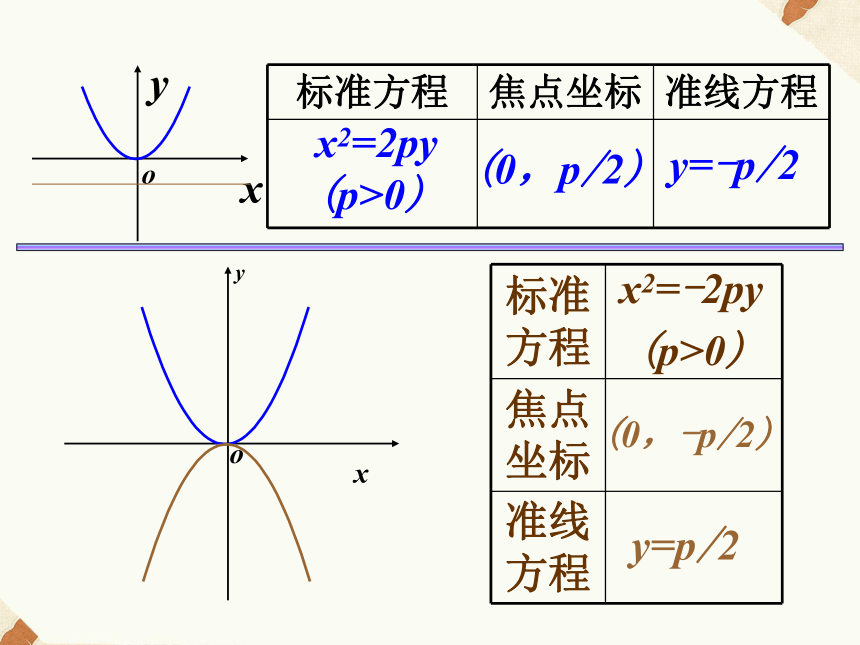
(p>0)x2=2py (p>0)(0,p/2)y=-p/2(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2, 0)y=-p/2x=p/2(-p/2, 0)x=-p/2抛物线的标准方程的四种形式:我们以前学习的抛物线和现在学习的抛物线的标准方程有什么联系?(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;例 1(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;解:方程可化为:故焦点坐标为 ,准线方程为(3) 已知抛物线的焦点坐标是F (0,-2)
求它的标准方程.解: 因焦点在y轴的负半轴上,故其标准方程为: x 2 = - 8yp=4(2)准线方程 是 x = ;(3)焦点到准线的距离是2.y2 =xy2 =4x 或 y2 = -4x
x2 =4y 或 x2 = -4y(1)焦点是F(3,0);y2 =12x(1)p=6,焦点坐标是(3,0)
准线方程是x=-3.(2)先化为标准方程 , ,
焦点坐标是(0, ),准线方程是y=- .解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2) 代入y2 = -2px,
得p= ∴抛物线的标准方程为 x2 = y或 y2 = x oyxABF解:如图,建立直角坐标系,设抛物线的标准方程是
y2=2px(p>0).易知A (0.5,2.4),代入方程得p=5.76.2.42=2p×0.5所以,所求抛物线为y2=11.52x,
焦点坐标为(2.88,0).如图可知原条件等价于
M点到F(4,0)和到
x=-4距离相等,解:由抛物线的定义,
点M的轨迹是
以F(4,0)为焦点,
x=-4为准线的抛物线.因为p/2=4,所以p=8,
所求方程是y2=16x.M是抛物线y2 = 2px(p>0)上一点,
若点M 的横坐标为x0,
则点M到焦点的距离是练习4 抛物线 y2 = 2px ( p>0 ) 上一点M
到焦点的距离是 a ( a > ),
则点M到准线的距离是 ,
点 M的横坐标是 .练习5a练习6抛物线 y 2 =12 x 上与焦点的距离
等于9的点的坐标是 .y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2, 0)y=-p/2x=p/2(-p/2, 0)x=-p/2小结
抛物线及其标准方程第2章 圆锥曲线与方程生活中的抛物线抛物线模型抛物线碟形天线抛物线灯一条抛物线.其顶点坐标是什么?对称轴是什么?我们怎么画一条抛物线呢?动画二次函数y=ax2+bx+c(a≠0)的图象是 平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线定点F叫做抛物线的焦点.定直线l叫做抛物线的准线. 抛物线的定义:如何建立适当的
直角坐标系?那么焦点F的坐标为(p/2,0),lFKMNoyx标准方程的推导1、建系设F在直线l上的垂足为K,以FK的中点为坐标原点,以KF为x轴,建立直角坐标系.2、设点设|KF|=p(p>0),准线l上的方程为lFKMNoyx3、列式设M(x,y),点M到l的距离为d,由抛物线的定义知抛物线就是点的集合即:4、化简此方程叫抛物线的标准方程.焦点F的坐标为(p/2,0),准线l上的方程为其中p的几何意义是:
焦点到准线的距离.说明一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.xyoy2=-2px
(p>0)(-p/2,0)x=p/2y2=2px (p>0)(p/2,0)x=-p/2xyox2=2py(p>0)(0,p/2)y=-p/2y2=2px (p>0)(p/2,0)x=-p/2xyox2=-2py
(p>0)x2=2py (p>0)(0,p/2)y=-p/2(0,-p/2)y=p/2y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2, 0)y=-p/2x=p/2(-p/2, 0)x=-p/2抛物线的标准方程的四种形式:我们以前学习的抛物线和现在学习的抛物线的标准方程有什么联系?(1)已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;例 1(2)已知抛物线的方程是y = -6x2,
求它的焦点坐标和准线方程;解:方程可化为:故焦点坐标为 ,准线方程为(3) 已知抛物线的焦点坐标是F (0,-2)
求它的标准方程.解: 因焦点在y轴的负半轴上,故其标准方程为: x 2 = - 8yp=4(2)准线方程 是 x = ;(3)焦点到准线的距离是2.y2 =xy2 =4x 或 y2 = -4x
x2 =4y 或 x2 = -4y(1)焦点是F(3,0);y2 =12x(1)p=6,焦点坐标是(3,0)
准线方程是x=-3.(2)先化为标准方程 , ,
焦点坐标是(0, ),准线方程是y=- .解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2) 代入y2 = -2px,
得p= ∴抛物线的标准方程为 x2 = y或 y2 = x oyxABF解:如图,建立直角坐标系,设抛物线的标准方程是
y2=2px(p>0).易知A (0.5,2.4),代入方程得p=5.76.2.42=2p×0.5所以,所求抛物线为y2=11.52x,
焦点坐标为(2.88,0).如图可知原条件等价于
M点到F(4,0)和到
x=-4距离相等,解:由抛物线的定义,
点M的轨迹是
以F(4,0)为焦点,
x=-4为准线的抛物线.因为p/2=4,所以p=8,
所求方程是y2=16x.M是抛物线y2 = 2px(p>0)上一点,
若点M 的横坐标为x0,
则点M到焦点的距离是练习4 抛物线 y2 = 2px ( p>0 ) 上一点M
到焦点的距离是 a ( a > ),
则点M到准线的距离是 ,
点 M的横坐标是 .练习5a练习6抛物线 y 2 =12 x 上与焦点的距离
等于9的点的坐标是 .y2=2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,-p/2)(p/2, 0)y=-p/2x=p/2(-p/2, 0)x=-p/2小结
