2.3.2 抛物线的简单几何性质 课件1
文档属性
| 名称 | 2.3.2 抛物线的简单几何性质 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 223.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 10:51:45 | ||
图片预览







文档简介
课件29张PPT。第二章 圆锥曲线与方程2.3.2 抛物线的简单几何性质准线方程焦点坐标标准方程图 形y2=2px
(p>0)x2=2py
(p>0)x2= -2py
(p>0)y2= -2px
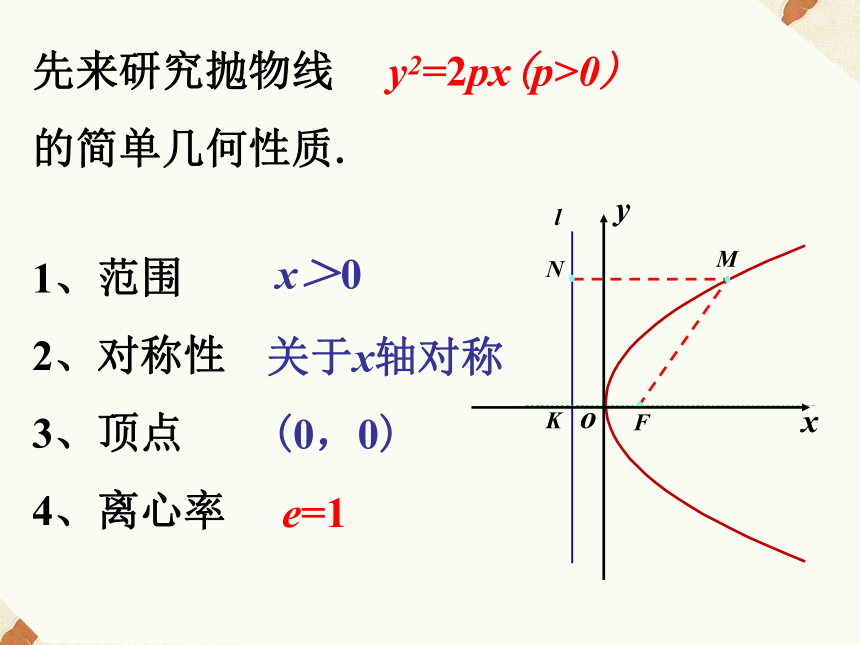
(p>0)先来研究抛物线 y2=2px(p>0)
的简单几何性质.lFKMNoyx1、范围
2、对称性
3、顶点
4、离心率 x>0关于x轴对称(0,0)e=1对称轴顶点坐标范 围图 形x≥0( 0 , 0 )y=0( 0 , 0 )y=0y≥0x=0y≤0( 0 , 0 )x≤0( 0 , 0 )x=0 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点 M( ) ,求它的标准方程,并用描点法画出图形.所以可设它的标准方程
为y2=2px(p>0)解:因为抛物线关于x轴对称,
它的顶点在原点,
并且过M( )例 1 因为点M在抛物线上,
所以即: p=2.因此所求抛物线的方程为 y2=4x.xyoM 求适合下列条件的抛物线方程:
(1) 顶点在原点,关于x 轴对称,并且经过点M(5,-4) ;
(2) 顶点在原点,焦点是F(0,5) ;
(3) 顶点在原点,准线是 x=4;
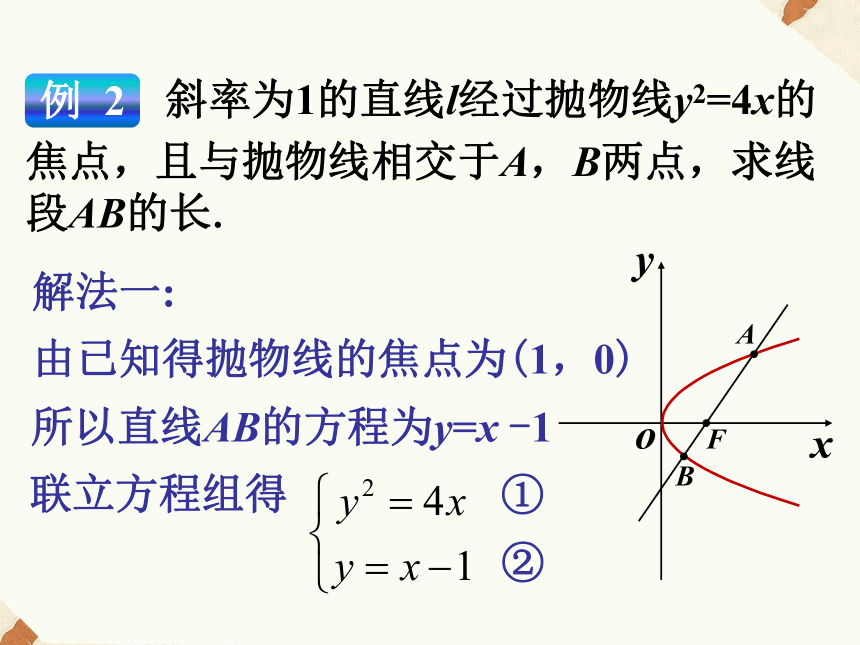
(4) 焦点是F(0,-8),准线是 y=8.练习1 先定型,再定量例 2 斜率为1的直线l经过抛物线y2=4x的
焦点,且与抛物线相交于A,B两点,求线段AB的长.解法一:
由已知得抛物线的焦点为(1,0)xoyBFA所以直线AB的方程为y=x -1整理得 x2-6x+1=0解得: ,将x1 , x2代入y=x-1得AB坐标为A B由两点间距离公式得:AB=8 .②代入①得 (x-1)2=4xxoyBFAdBxoyBFAB’A’解法二:如图设A(x1,y1),B(x2,y2),A,B到准线的距离分别为dA,dB,由已知得抛物线的焦点为(1,0)所以直线AB的方程为
y=x -1 ① 由抛物线的定义
可知 |AF|=dA=x1+1, |BF|=dB=x2+1,于是|AB|=|AF|+|BF|=x1+x2+2dAxoyBFAB’A’整理得 x2-6x+1=0解得: ,于是 |AB|=x1+x2+2=8所以线段的长是8.试比较两种解法将①代入方程y2=4x,得(x-1)2=4x依照上题的思路:xA+xB=4所以xM=2将xM=2代入 y=x-1得yM=1所以M为(2,1)oxy相离相切相交复位回顾:直线与圆的位置关系如何从式子中解得直线与圆的关系?把直线方程代入圆的方程得到一元二次方程计 算 判 别 式思考:直线与抛物线有多少种位置关系.复位相离相切相交1相交2直线与抛物线的位置关系.1、求直线 y = x -1与抛物线 y2 =4x
的位置关系.练习3 相 交注:得到一元二次方程,需计算判别式.2、求直线 y = 6与抛物线 y2 =4x
的位置关系.相 交注:得到一元一次方程,得到一个交点. 已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k.当k为何值时,直线l与抛物线:只有一个公共点;有两个公共点;没有公共点.例 3 PP可得 ky2-4y+4(2k+1)=0 (П)把y=1代入y2=4x , 得这时,直线l与抛物线只有一个公共点 (1/4 , 1 )(2)当k≠0时,方程(П)的
判别式为△=-16(2k2+k-1)下面分三种情况讨论.① 由△ =0,即2k2+k-1=0
解得k=-1或k=1/2于是,当k=-1或k=1/2时,
方程(П)只有一个解,
从而方程组(?)只有一个解,
这时,直线l与抛物线只有一个公共点②由△>0,即 2k2 + k -1<0
解得 -1方程(П)有2个解
从而方程组(?)有2个解.
这时,直线l与抛物线有2个公共点.③由△<0,即 2k2+k-1>0
解得 k<-1或k>1/2于是,当k<-1或k>1/2时,
方程(П) 没有实数解,
从而方程组(?) 没有解.
这时,直线l与抛物线没有公共点.综上可得:
当k=-1或k=1/2或k=0时,
直线l与抛物线只有一个公共点
当-1直线l与抛物线有2个公共点.
当k<-1或k>1/2时
直线l与抛物线没有公共点.PP判断位置关系方法总结把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式此方法适用于其他各种曲线直线与抛物线的位置关系直线与抛物线的位置关系的判断方法小 结:抛物线的简单几何性质
(p>0)x2=2py
(p>0)x2= -2py
(p>0)y2= -2px
(p>0)先来研究抛物线 y2=2px(p>0)
的简单几何性质.lFKMNoyx1、范围
2、对称性
3、顶点
4、离心率 x>0关于x轴对称(0,0)e=1对称轴顶点坐标范 围图 形x≥0( 0 , 0 )y=0( 0 , 0 )y=0y≥0x=0y≤0( 0 , 0 )x≤0( 0 , 0 )x=0 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点 M( ) ,求它的标准方程,并用描点法画出图形.所以可设它的标准方程
为y2=2px(p>0)解:因为抛物线关于x轴对称,
它的顶点在原点,
并且过M( )例 1 因为点M在抛物线上,
所以即: p=2.因此所求抛物线的方程为 y2=4x.xyoM 求适合下列条件的抛物线方程:
(1) 顶点在原点,关于x 轴对称,并且经过点M(5,-4) ;
(2) 顶点在原点,焦点是F(0,5) ;
(3) 顶点在原点,准线是 x=4;
(4) 焦点是F(0,-8),准线是 y=8.练习1 先定型,再定量例 2 斜率为1的直线l经过抛物线y2=4x的
焦点,且与抛物线相交于A,B两点,求线段AB的长.解法一:
由已知得抛物线的焦点为(1,0)xoyBFA所以直线AB的方程为y=x -1整理得 x2-6x+1=0解得: ,将x1 , x2代入y=x-1得AB坐标为A B由两点间距离公式得:AB=8 .②代入①得 (x-1)2=4xxoyBFAdBxoyBFAB’A’解法二:如图设A(x1,y1),B(x2,y2),A,B到准线的距离分别为dA,dB,由已知得抛物线的焦点为(1,0)所以直线AB的方程为
y=x -1 ① 由抛物线的定义
可知 |AF|=dA=x1+1, |BF|=dB=x2+1,于是|AB|=|AF|+|BF|=x1+x2+2dAxoyBFAB’A’整理得 x2-6x+1=0解得: ,于是 |AB|=x1+x2+2=8所以线段的长是8.试比较两种解法将①代入方程y2=4x,得(x-1)2=4x依照上题的思路:xA+xB=4所以xM=2将xM=2代入 y=x-1得yM=1所以M为(2,1)oxy相离相切相交复位回顾:直线与圆的位置关系如何从式子中解得直线与圆的关系?把直线方程代入圆的方程得到一元二次方程计 算 判 别 式思考:直线与抛物线有多少种位置关系.复位相离相切相交1相交2直线与抛物线的位置关系.1、求直线 y = x -1与抛物线 y2 =4x
的位置关系.练习3 相 交注:得到一元二次方程,需计算判别式.2、求直线 y = 6与抛物线 y2 =4x
的位置关系.相 交注:得到一元一次方程,得到一个交点. 已知抛物线的方程为y2=4x,直线l过定点P(-2,1),斜率为k.当k为何值时,直线l与抛物线:只有一个公共点;有两个公共点;没有公共点.例 3 PP可得 ky2-4y+4(2k+1)=0 (П)把y=1代入y2=4x , 得这时,直线l与抛物线只有一个公共点 (1/4 , 1 )(2)当k≠0时,方程(П)的
判别式为△=-16(2k2+k-1)下面分三种情况讨论.① 由△ =0,即2k2+k-1=0
解得k=-1或k=1/2于是,当k=-1或k=1/2时,
方程(П)只有一个解,
从而方程组(?)只有一个解,
这时,直线l与抛物线只有一个公共点②由△>0,即 2k2 + k -1<0
解得 -1
从而方程组(?)有2个解.
这时,直线l与抛物线有2个公共点.③由△<0,即 2k2+k-1>0
解得 k<-1或k>1/2于是,当k<-1或k>1/2时,
方程(П) 没有实数解,
从而方程组(?) 没有解.
这时,直线l与抛物线没有公共点.综上可得:
当k=-1或k=1/2或k=0时,
直线l与抛物线只有一个公共点
当-1
当k<-1或k>1/2时
直线l与抛物线没有公共点.PP判断位置关系方法总结把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交(一个交点)计算判别式此方法适用于其他各种曲线直线与抛物线的位置关系直线与抛物线的位置关系的判断方法小 结:抛物线的简单几何性质
