3.1.2 导数的概念 课件2
文档属性
| 名称 | 3.1.2 导数的概念 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 179.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览



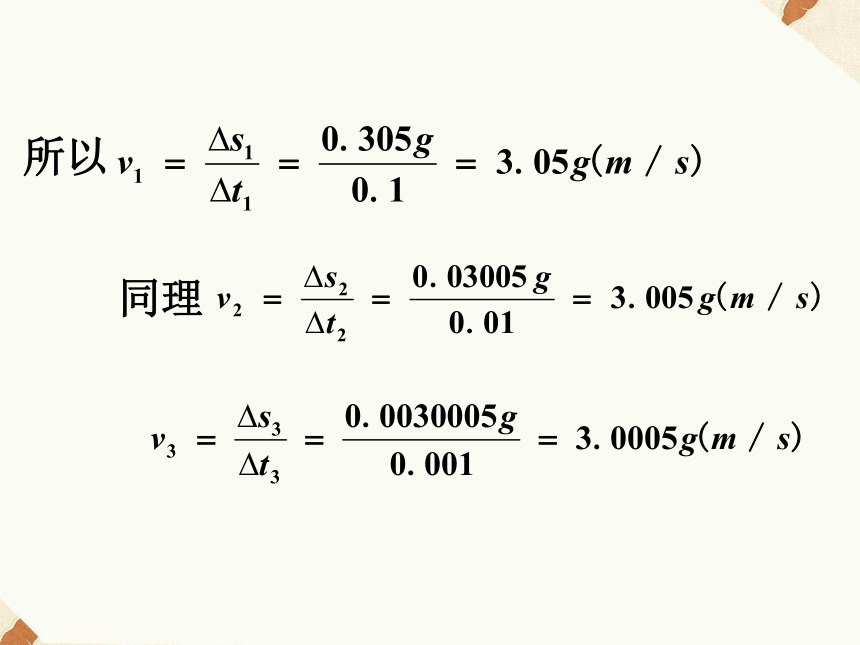





文档简介
课件28张PPT。第三章 导数及其应用3.1.2 导数的概念自由落体运动中,物体在不同时刻的
速度是不一样的.平均速度不一定能反映物体在某一时刻
的运动情况.物体在某一时刻的速度称为瞬时速度.解:设在[3,3.1]内的平均速度为v1,则△t1=3.1-3=0.1(s)△s1=s(3.1)-s(3)= 0.5g× 3.12-0.5g×32
=0.305g(m)所以同理例1是计算了[3,3+△t]当t=0.1,t=0.01,t=0.001时的平均速度.上面是计算了△t>0时的情况下面再来计算△t<0时的情况解:设在[2.9,3]内的平均速度为v4,则△t1=3-2.9=0.1(s)△s1=s(3)-s(2.9)= 0.5g×32-0.5g×2.92=0.295g(m)所以设在[2.99,3]内的平均速度为v5,则设在[2.999,3]内的平均速度为v6,则当△t→0时,
物体的速度趋近于一个确定的值3g在 t=3s 这一时刻的瞬时速度等于
在 3s 到 (3+△t)s 这段时间内的平均速度
当△t→0的极限, 设物体的运动方程是 s=s(t),
物体在时刻 t 的瞬时速度为 v , 一般结论就是物体在 t 到 t+△t 这段时间内,
当△t→0 时平均速度的极限 ,即 让我们再来看一个例子P相切相交再来一次例2P再来一次设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P及P点邻近的任一点
Q(x0+△x,y0+△y) , 过P,Q两点作割线,
则直线PQ的斜率为上面我们研究了切线的斜率问题,可以将以上的过程概括如下:当直线PQ转动时,Q逐渐向P靠近,
也即△x 变小当△x→0时,PQ无限靠近PT因此:一般地,
函数y=f(x)在x=x0处的瞬时变化率是上式称为函数y=f(x)在x=x0处的导数记作: 或 即注意:1、函数应在点的附近有定义,
否则导数不存在. 2、在定义导数的极限式中,△x趋近于0
可正、可负,但不为0,而△y可能为0.3、导数是一个局部概念,它只与函数在x0
及其附近的函数值有关,与△x无关.4、若极限 不存在,则称
函数在点x0处不可导.
物体的运动方程 s=s(t)在t0处的导数
即在t0处的瞬时速度vt0函数y=f(x)在x0处的导数
即曲线在x0处的切线斜率.导数可以描述任何事物的瞬时变化率.瞬时变化率除了瞬时速度,切线的斜率还有:点密度,国内生产总值(GDP)的增
长率,经济学上讲的一切边际量等.例1、将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热.如果第xh时,原油的温度(单位:℃)为f(x)=x2-7x+15 (0?x ?8).计算第2h和第6h时,原油温度的瞬进变化率,并说明它们的意义.解:第2h和第6h时,原油温度的
瞬进变化率就是f ' (2)和f ' (6)根据导数定义:所以,同理可得 f '(6)=5f(x)=x2-7x+15 f '(6)=5 说明在第6h附近,原油温度
大约以5 ℃/h的速度上升;说明在第2h附近,原油温度
大约以3 ℃/h的速度下降;所以
物体在时刻t0处的瞬时速度为v0-gt0.由导数的定义可知,求函数y=f(x)在
点x0处的导数的方法是: (2)求平均变化率(3)取极限,得导数(1)求函数的增量练习2、质点按规律s(t)=at2+1做直线运动
(位移单位:m , 时间单位:s).若质点在
t=2时的瞬时速度为8m/s,求常数a的值.a=2由导数的定义可知,求函数y=f(x)在
点x0处的导数的方法是:
(1)求函数的增量
(2)求平均变化率
(3)取极限,得导数小 结:函数y=f(x)在x=x0处的瞬时变化率
的定义.
速度是不一样的.平均速度不一定能反映物体在某一时刻
的运动情况.物体在某一时刻的速度称为瞬时速度.解:设在[3,3.1]内的平均速度为v1,则△t1=3.1-3=0.1(s)△s1=s(3.1)-s(3)= 0.5g× 3.12-0.5g×32
=0.305g(m)所以同理例1是计算了[3,3+△t]当t=0.1,t=0.01,t=0.001时的平均速度.上面是计算了△t>0时的情况下面再来计算△t<0时的情况解:设在[2.9,3]内的平均速度为v4,则△t1=3-2.9=0.1(s)△s1=s(3)-s(2.9)= 0.5g×32-0.5g×2.92=0.295g(m)所以设在[2.99,3]内的平均速度为v5,则设在[2.999,3]内的平均速度为v6,则当△t→0时,
物体的速度趋近于一个确定的值3g在 t=3s 这一时刻的瞬时速度等于
在 3s 到 (3+△t)s 这段时间内的平均速度
当△t→0的极限, 设物体的运动方程是 s=s(t),
物体在时刻 t 的瞬时速度为 v , 一般结论就是物体在 t 到 t+△t 这段时间内,
当△t→0 时平均速度的极限 ,即 让我们再来看一个例子P相切相交再来一次例2P再来一次设曲线C是函数 y=f(x) 的图象,
在曲线C上取一点 P及P点邻近的任一点
Q(x0+△x,y0+△y) , 过P,Q两点作割线,
则直线PQ的斜率为上面我们研究了切线的斜率问题,可以将以上的过程概括如下:当直线PQ转动时,Q逐渐向P靠近,
也即△x 变小当△x→0时,PQ无限靠近PT因此:一般地,
函数y=f(x)在x=x0处的瞬时变化率是上式称为函数y=f(x)在x=x0处的导数记作: 或 即注意:1、函数应在点的附近有定义,
否则导数不存在. 2、在定义导数的极限式中,△x趋近于0
可正、可负,但不为0,而△y可能为0.3、导数是一个局部概念,它只与函数在x0
及其附近的函数值有关,与△x无关.4、若极限 不存在,则称
函数在点x0处不可导.
物体的运动方程 s=s(t)在t0处的导数
即在t0处的瞬时速度vt0函数y=f(x)在x0处的导数
即曲线在x0处的切线斜率.导数可以描述任何事物的瞬时变化率.瞬时变化率除了瞬时速度,切线的斜率还有:点密度,国内生产总值(GDP)的增
长率,经济学上讲的一切边际量等.例1、将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热.如果第xh时,原油的温度(单位:℃)为f(x)=x2-7x+15 (0?x ?8).计算第2h和第6h时,原油温度的瞬进变化率,并说明它们的意义.解:第2h和第6h时,原油温度的
瞬进变化率就是f ' (2)和f ' (6)根据导数定义:所以,同理可得 f '(6)=5f(x)=x2-7x+15 f '(6)=5 说明在第6h附近,原油温度
大约以5 ℃/h的速度上升;说明在第2h附近,原油温度
大约以3 ℃/h的速度下降;所以
物体在时刻t0处的瞬时速度为v0-gt0.由导数的定义可知,求函数y=f(x)在
点x0处的导数的方法是: (2)求平均变化率(3)取极限,得导数(1)求函数的增量练习2、质点按规律s(t)=at2+1做直线运动
(位移单位:m , 时间单位:s).若质点在
t=2时的瞬时速度为8m/s,求常数a的值.a=2由导数的定义可知,求函数y=f(x)在
点x0处的导数的方法是:
(1)求函数的增量
(2)求平均变化率
(3)取极限,得导数小 结:函数y=f(x)在x=x0处的瞬时变化率
的定义.
