3.1.3 导数的几何意义 课件1
文档属性
| 名称 | 3.1.3 导数的几何意义 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 11:00:55 | ||
图片预览




文档简介
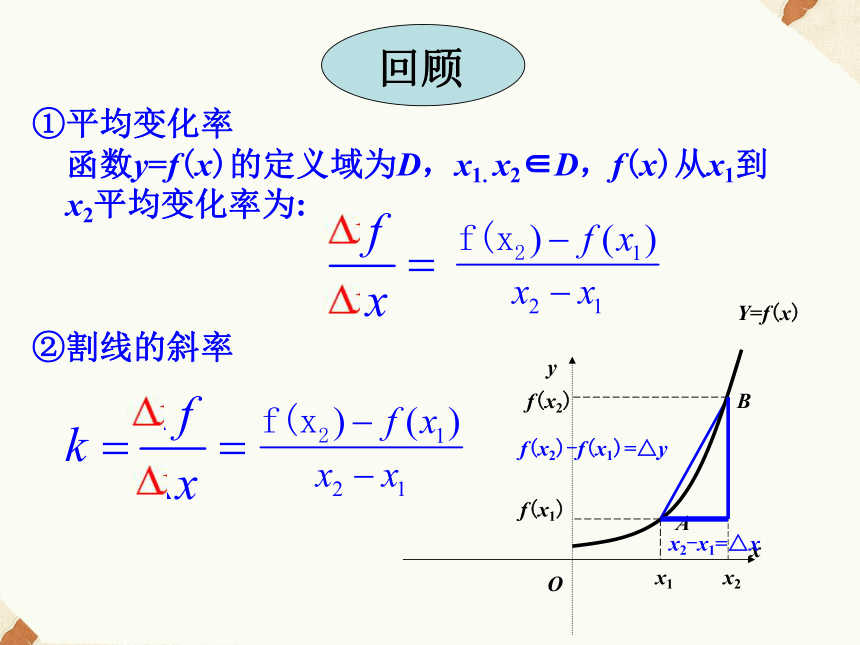
课件17张PPT。3.1.3导数的几何意义①平均变化率函数y=f(x)的定义域为D,x1.x2∈D,f(x)从x1到x2平均变化率为:②割线的斜率以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似值过渡到瞬时速度的精确值.我们把物体在某一时刻的速度称为瞬时速度.从函数y=f(x)在x=x0处的瞬时变化率是:以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似值过渡到瞬时速度的精确值.我们把物体在某一时刻的速度称为瞬时速度.从函数y=f(x)在x=x0处的瞬时变化率是: 由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
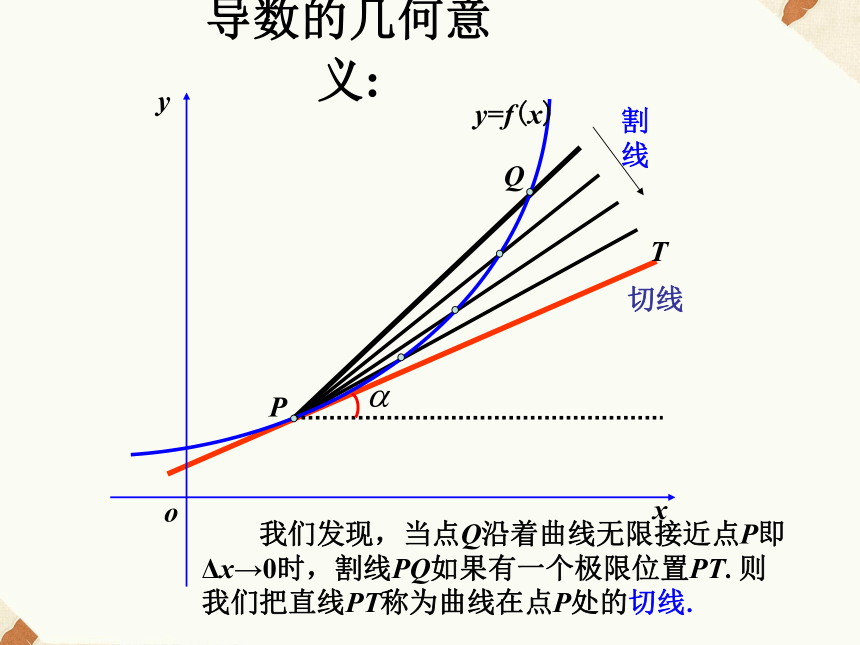
哪种形式, Δy也必须选择与之相对应的形式.回顾PQ割线切线T导数的几何意义: 我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即:这个概念: ①提供了求曲线上某点切线的斜
率的一种方法;
②切线斜率的本质——函数在x=x0处的导数. 要注意,曲线在某点处的切线:
1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,
可以有多个,甚至可以无穷多个.因此,切线方程为y-2=2(x-1),
即y=2x.求曲线在某点处的切线方程
的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求
出切线的斜率;
③利用点斜式求切线方程.练习:如图已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.在不致发生混淆时,导函数也简称导数.函数导函数由函数f(x)在x=x0处求导数的过程可以看到,当时,f’(x0) 是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:如何求函数y=f(x)的导数?看一个例子:下面把前面知识小结:a.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态. b.要切实掌握求导数的三个步骤:
(1)求函数的增 量;
(2)求平均变化率;
(3)取极限,得导数.(3)函数f(x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 .这也是
求函数在点x0处的导数的方法之一. 小结:(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 .(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数.c.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数” 之间的区别与联系.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率.(2)根据直线方程的点斜式写出切线方程,即d.求切线方程的步骤:小结: 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念.
作业:P79-80 A组 4,5,6.(其中6题作在书上,
B组1,2,3题作在书上)
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.回顾PQ割线切线T导数的几何意义: 我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.即:这个概念: ①提供了求曲线上某点切线的斜
率的一种方法;
②切线斜率的本质——函数在x=x0处的导数. 要注意,曲线在某点处的切线:
1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,
可以有多个,甚至可以无穷多个.因此,切线方程为y-2=2(x-1),
即y=2x.求曲线在某点处的切线方程
的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求
出切线的斜率;
③利用点斜式求切线方程.练习:如图已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.即点P处的切线的斜率等于4. (2)在点P处的切线方程是y-8/3=4(x-2),即12x-3y-16=0.在不致发生混淆时,导函数也简称导数.函数导函数由函数f(x)在x=x0处求导数的过程可以看到,当时,f’(x0) 是一个确定的数.那么,当x变化时,便是x的一个函数,我们叫它为f(x)的导函数.即:如何求函数y=f(x)的导数?看一个例子:下面把前面知识小结:a.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态. b.要切实掌握求导数的三个步骤:
(1)求函数的增 量;
(2)求平均变化率;
(3)取极限,得导数.(3)函数f(x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 .这也是
求函数在点x0处的导数的方法之一. 小结:(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 .(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数.c.弄清“函数f(x)在点x0处的导数”、“导函数”、“导数” 之间的区别与联系.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率.(2)根据直线方程的点斜式写出切线方程,即d.求切线方程的步骤:小结: 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念.
作业:P79-80 A组 4,5,6.(其中6题作在书上,
B组1,2,3题作在书上)
