3.1.3 导数的几何意义 课件3
文档属性
| 名称 | 3.1.3 导数的几何意义 课件3 |
|
|
| 格式 | zip | ||
| 文件大小 | 214.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览





文档简介
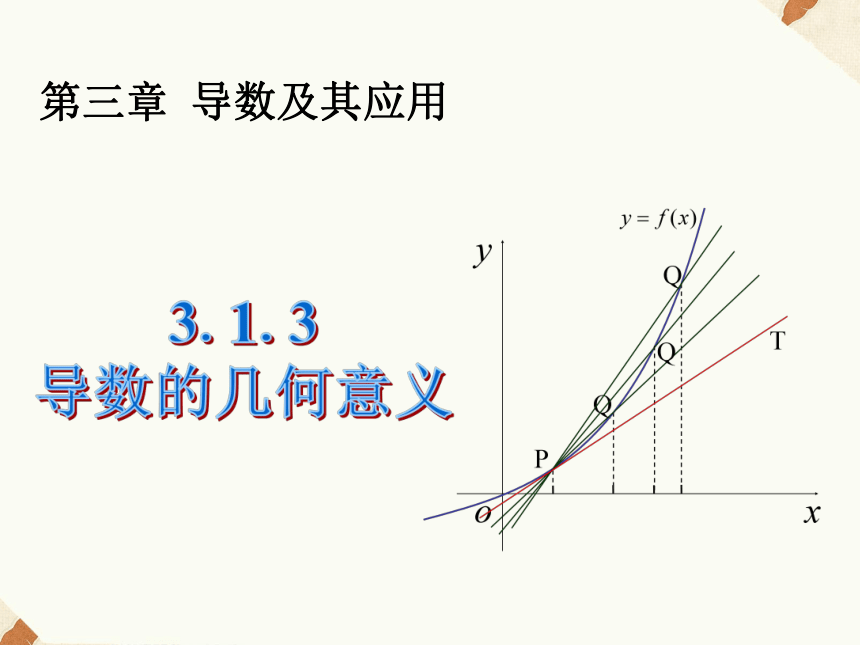
课件19张PPT。第三章 导数及其应用3.1.3
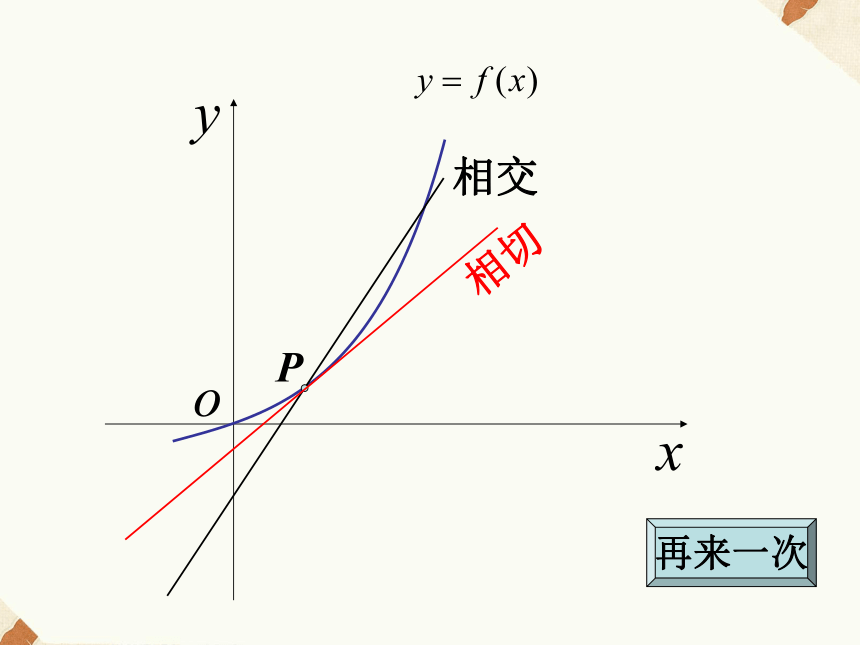
导数的几何意义P相切相交再来一次直线PQ的斜率为PQ无限靠近切线PT相应的 ,
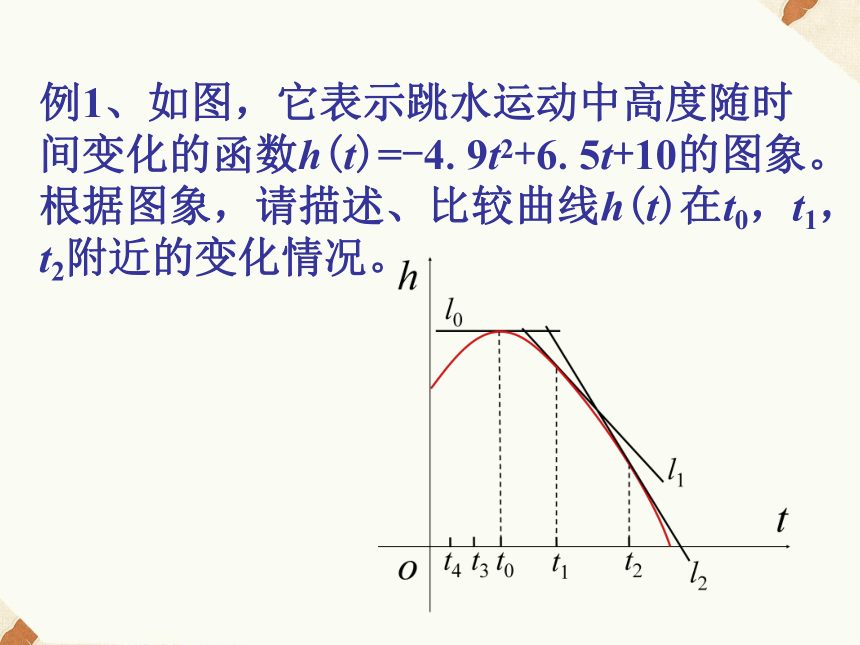
y=f(x)在点P( x0,f(x0) )处的切线方程为:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.例1、如图,它表示跳水运动中高度随时间变化的函数h(t)=-4.9t2+6.5t+10的图象。根据图象,请描述、比较曲线h(t)在t0,t1,t2附近的变化情况。解:我们用曲线h(t)在t0,t1,t2处的切线,
刻画曲线h(t)在上述三个时刻附近的
变化情况。 当t=t0时,曲线h(t)在t0处的切线l0平行
于x轴. 所以,在t=t0附近曲线比较平坦,
几乎没有下降. 当t=t1时,曲线h(t)在t1处的切线l1的斜率
h′(t1)<0. 所以,在t=t1附近曲线下降,
即函数h(t)在t=t1附近单调递减. (3) 当t=t2时,曲线h(t)在t2处的切线l2的斜率
h′(t2)<0. 所以,在t=t2附近曲线下降,
即函数h(t)在t=t2附近也单调递减. 与t2相比,曲线在t1附近下降得缓慢些.例2、如图,它表示人体血管中药物浓度c=f(t)(单位:mg/mL)随时间t(单位:min)变化的函数图象。根据图象,估计t=
0.5,0.8时,血管中药物浓度的瞬时变化率(精确到0.1)00.20.10.40.60.51.10.70.31.00.90.80.20.10.40.60.51.10.70.31.00.90.8t(min)c(mg/mL)解:血管中某一时刻药物浓度的瞬时变化
率,就是药物浓度f(t)在此时刻的导数。作t=0.5处的切线,它的斜率约为0所以,作t=0.8处的切线,它的斜率约为-1.5所以,因此在t=0.5和0.8处药物浓度的瞬时
变化率分别为0和-1.5.
求函数y=f(x)在点x0处的导数的方法是: (2)求平均变化率(3)取极限,得导数(1)求函数的增量回顾例3、某物体的运动方程为s(t)=5t2
(位移单位:m,时间单位:s)
求它在 t=2s 时的速度.解: 因为从而所以例4、已知曲线 上一点
求:点P处的切线的斜率;
点P处的的切线方程. 解: 点P处的切线的斜率即
在x=2处的导数.因为从而所以点P处的的切线方程点P处的切线的斜率是4.即直线练习1、求曲线 在点M(3,3)处的
切线的斜率及倾斜角.斜率为-1,倾斜角为135°有,切线的方程为注: 学了导数的运算后,
此类题有更简单的解法.如果将x0改为x,则求得的是被称为函数y=f(x)的导函数.如果函数y=f(x)在开区间(a,b)内的每点处都有导数,此时对于每一个x∈(a,b),都对应着一个确定的导数 ,从而构成了一个新的函数 。称这个函数 为函数y=f(x)在开区间内的导函数,简称导数,也可记作 ,即==小 结:相应的 ,
y=f(x)在点P( x0,f(x0) )处的切线方程为:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.
导数的几何意义P相切相交再来一次直线PQ的斜率为PQ无限靠近切线PT相应的 ,
y=f(x)在点P( x0,f(x0) )处的切线方程为:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.例1、如图,它表示跳水运动中高度随时间变化的函数h(t)=-4.9t2+6.5t+10的图象。根据图象,请描述、比较曲线h(t)在t0,t1,t2附近的变化情况。解:我们用曲线h(t)在t0,t1,t2处的切线,
刻画曲线h(t)在上述三个时刻附近的
变化情况。 当t=t0时,曲线h(t)在t0处的切线l0平行
于x轴. 所以,在t=t0附近曲线比较平坦,
几乎没有下降. 当t=t1时,曲线h(t)在t1处的切线l1的斜率
h′(t1)<0. 所以,在t=t1附近曲线下降,
即函数h(t)在t=t1附近单调递减. (3) 当t=t2时,曲线h(t)在t2处的切线l2的斜率
h′(t2)<0. 所以,在t=t2附近曲线下降,
即函数h(t)在t=t2附近也单调递减. 与t2相比,曲线在t1附近下降得缓慢些.例2、如图,它表示人体血管中药物浓度c=f(t)(单位:mg/mL)随时间t(单位:min)变化的函数图象。根据图象,估计t=
0.5,0.8时,血管中药物浓度的瞬时变化率(精确到0.1)00.20.10.40.60.51.10.70.31.00.90.80.20.10.40.60.51.10.70.31.00.90.8t(min)c(mg/mL)解:血管中某一时刻药物浓度的瞬时变化
率,就是药物浓度f(t)在此时刻的导数。作t=0.5处的切线,它的斜率约为0所以,作t=0.8处的切线,它的斜率约为-1.5所以,因此在t=0.5和0.8处药物浓度的瞬时
变化率分别为0和-1.5.
求函数y=f(x)在点x0处的导数的方法是: (2)求平均变化率(3)取极限,得导数(1)求函数的增量回顾例3、某物体的运动方程为s(t)=5t2
(位移单位:m,时间单位:s)
求它在 t=2s 时的速度.解: 因为从而所以例4、已知曲线 上一点
求:点P处的切线的斜率;
点P处的的切线方程. 解: 点P处的切线的斜率即
在x=2处的导数.因为从而所以点P处的的切线方程点P处的切线的斜率是4.即直线练习1、求曲线 在点M(3,3)处的
切线的斜率及倾斜角.斜率为-1,倾斜角为135°有,切线的方程为注: 学了导数的运算后,
此类题有更简单的解法.如果将x0改为x,则求得的是被称为函数y=f(x)的导函数.如果函数y=f(x)在开区间(a,b)内的每点处都有导数,此时对于每一个x∈(a,b),都对应着一个确定的导数 ,从而构成了一个新的函数 。称这个函数 为函数y=f(x)在开区间内的导函数,简称导数,也可记作 ,即==小 结:相应的 ,
y=f(x)在点P( x0,f(x0) )处的切线方程为:函数y=f(x)在点x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,f(x0))处的切线的斜率.
