3.2.1 几个常用函数的导数 课件2
文档属性
| 名称 | 3.2.1 几个常用函数的导数 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览




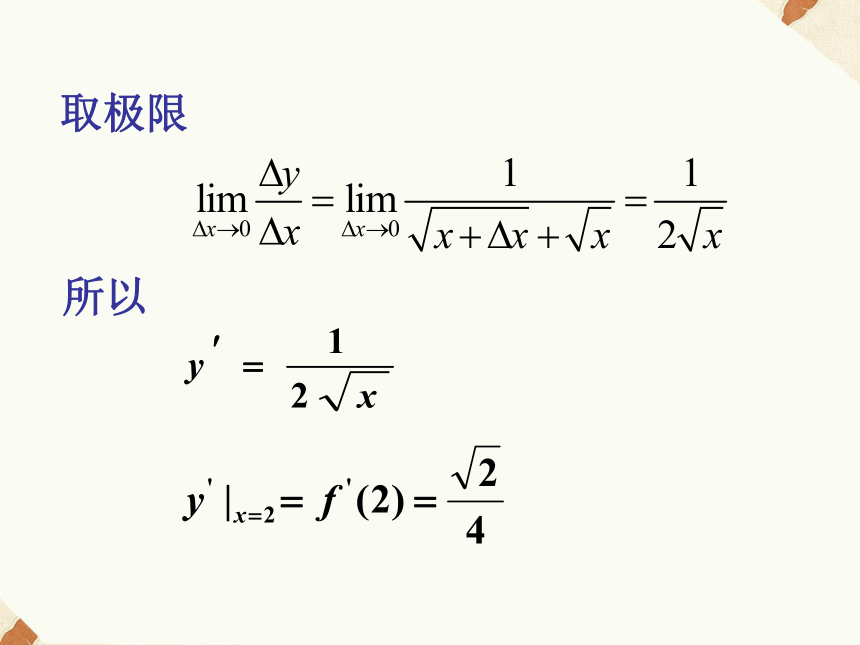


文档简介
课件14张PPT。第三章 导数及其应用3.2.1
几个常用函数的导数如果将x0改为x,则求得的是被称为函数y=f(x)的导函数.复习回顾如果函数y=f(x)在开区间(a,b)内的每点处都有导数,此时对于每一个x∈(a,b),都对应着一个确定的导数 ,从而构成了一个新的函数 .称这个函数 为函数y=f(x)在开区间内的导函数,简称导数,也可记作 ,即==例1:已知函数 y =
(1)求y'
(2)求函数 y = 在 x = 2 处的导数解:函数改变量算比值取极限所以练习1、求函数y=f(x)=c的导数.因为所以因为所以练习2、求函数y=f(x)=x的导数因为所以练习3、求函数y=f(x)=x2的导数你能不能求出函数y=f(x)=x3的导数.思考y' =3x2你猜测 y = x n 导数是什么?y' =nxn-1因为所以例2、y=|x|(x∈R)有没有导函数,试求之. 解: (1)当x>0时,y=x, 则y' =1(2)当x<0时,y=-x,不难求得y' =-1(3)当x=0时,y=0,求其导数如下:当△x>0时,比值为1,从而极限为1当△x<0时,比值为-1,从而极限为-1从而当x=0时,极限不存在.故y=|x|(x∈R)没有导函数.结论:并不是每个函数都有导函数.试自己推导教材P90的公式3、公式4.你还能推导教材P90的其他公式吗?小 结:求一个函数的导函数的方法.
几个常用函数的导数如果将x0改为x,则求得的是被称为函数y=f(x)的导函数.复习回顾如果函数y=f(x)在开区间(a,b)内的每点处都有导数,此时对于每一个x∈(a,b),都对应着一个确定的导数 ,从而构成了一个新的函数 .称这个函数 为函数y=f(x)在开区间内的导函数,简称导数,也可记作 ,即==例1:已知函数 y =
(1)求y'
(2)求函数 y = 在 x = 2 处的导数解:函数改变量算比值取极限所以练习1、求函数y=f(x)=c的导数.因为所以因为所以练习2、求函数y=f(x)=x的导数因为所以练习3、求函数y=f(x)=x2的导数你能不能求出函数y=f(x)=x3的导数.思考y' =3x2你猜测 y = x n 导数是什么?y' =nxn-1因为所以例2、y=|x|(x∈R)有没有导函数,试求之. 解: (1)当x>0时,y=x, 则y' =1(2)当x<0时,y=-x,不难求得y' =-1(3)当x=0时,y=0,求其导数如下:当△x>0时,比值为1,从而极限为1当△x<0时,比值为-1,从而极限为-1从而当x=0时,极限不存在.故y=|x|(x∈R)没有导函数.结论:并不是每个函数都有导函数.试自己推导教材P90的公式3、公式4.你还能推导教材P90的其他公式吗?小 结:求一个函数的导函数的方法.
