3.2.2 基本初等函数的导数公式及导数的运算法则 课件1
文档属性
| 名称 | 3.2.2 基本初等函数的导数公式及导数的运算法则 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 857.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览







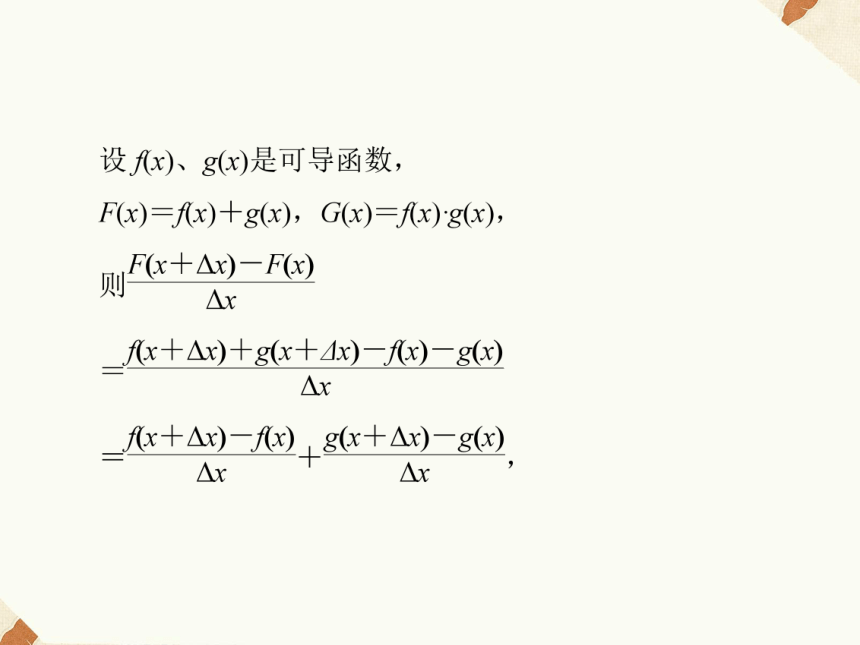
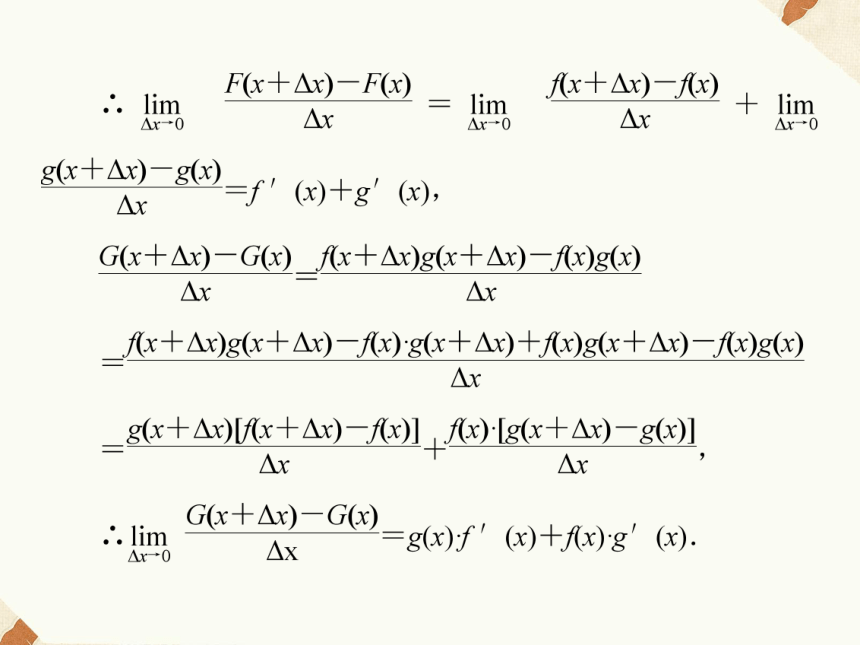



文档简介
课件31张PPT。圆锥曲线与方程第三章3.2 导数的计算
导数的运算法则第三章
能利用给出的基本初等函数的导数公式表和导数的四则运算法则求简单函数的导数.
重点:导数的四则运算法则及其运用.
难点:导数的四则运算法则的理解运用.思维导航
我们已经会求幂函数、指数函数、对数函数及y=sinx,y=cosx的导数,那么怎样求f(x)与g(x)的和、差、积、商的导数呢?导数的运算法则 新知导学
1.设函数f(x)、g(x)是可导函数,则:
(f(x)±g(x))′=________________;
(f(x)·g(x))′=_________________________.f ′(x)±g′(x)f ′(x)·g(x)+f(x)·g′(x)[答案] A
[解析] ∵f(x)=ax2+c,∴f′(x)=2ax,
又∵f′(1)=2a,∴2a=2,∴a=1.[答案] C3.求下列函数的导数
(1)y=2x2-3x+1,y′=________.
(2)y=(x+2)2,y′=________.
(3)y=sinx+cosx,y′=________.
(4)y=tanx,y′=________.
(5)y=(x+2)(3x-1),y′=________.导数的四则运算法则的应用 [解析] (1)∵y=ax2,∴y′=2ax,
∴抛物线在x=1处的切线的斜率2a,
∴2a=2,
∴a=1,故该抛物线方程为y=x2. 运用求导法则求切线方程 曲线y=2x-lnx-1在点(1,1)处的切线方程为( )
A.x-y=0 B.x+y-2=0
C.x+4y-5=0 D.x-4y-5=0
[答案] A利用导数求参数 [解析] ∵f(x)的图象过点P(0,1),∴e=1.
又∵f(x)为偶函数,∴f(-x)=f(x).
故ax4+bx3+cx2+dx+e=ax4-bx3+cx2-dx+e.
∴b=0,d=0.∴f(x)=ax4+cx2+1.[方法规律总结] 1.导数的应用中,求导数是一个基本解题环节,应仔细分析函数解析式的结构特征,根据导数公式及运算法则求导数,不具备导数运算法则的结构形式时,先恒等变形,然后分析题目特点,探寻条件与结论的联系,选择解题途径.
2.求参数的问题一般依据条件建立参数的方程求解.已知抛物线y=ax2+bx-7通过点(1,1),过点(1,1)的切线方程为4x-y-3=0,求a、b的值.
[解析] 由于抛物线y=ax2+bx-7经过点(1,1),
∴1=a+b-7,即a+b-8=0 ①
又由于经过点(1,1)的抛物线的切线方程为
4x-y-3=0,
∴经过该点的抛物线的切线斜率为4.
∵y′=(ax2+bx-7)′=2ax+b,∴2a+b-4=0. ②
由①、②解得a=-4,b=12.[辨析] 这是复合函数的导数,但复合函数的导数我们没有学习讨论过,遇到这种类型的函数求导,可先整理,再求导.
函数y=sin2x的导数为( )
A.y′=cos2x B.y′=2cos2x
C.y′=2(sin2x-cos2x) D.y′=-sin2x
[答案] B
[解析] y′=(sin2x)′=(2sinxcosx)′
=2(sinx)′·cosx+2sinx(cosx)′
=2cos2x-2sin2x=2cos2x.
导数的运算法则第三章
能利用给出的基本初等函数的导数公式表和导数的四则运算法则求简单函数的导数.
重点:导数的四则运算法则及其运用.
难点:导数的四则运算法则的理解运用.思维导航
我们已经会求幂函数、指数函数、对数函数及y=sinx,y=cosx的导数,那么怎样求f(x)与g(x)的和、差、积、商的导数呢?导数的运算法则 新知导学
1.设函数f(x)、g(x)是可导函数,则:
(f(x)±g(x))′=________________;
(f(x)·g(x))′=_________________________.f ′(x)±g′(x)f ′(x)·g(x)+f(x)·g′(x)[答案] A
[解析] ∵f(x)=ax2+c,∴f′(x)=2ax,
又∵f′(1)=2a,∴2a=2,∴a=1.[答案] C3.求下列函数的导数
(1)y=2x2-3x+1,y′=________.
(2)y=(x+2)2,y′=________.
(3)y=sinx+cosx,y′=________.
(4)y=tanx,y′=________.
(5)y=(x+2)(3x-1),y′=________.导数的四则运算法则的应用 [解析] (1)∵y=ax2,∴y′=2ax,
∴抛物线在x=1处的切线的斜率2a,
∴2a=2,
∴a=1,故该抛物线方程为y=x2. 运用求导法则求切线方程 曲线y=2x-lnx-1在点(1,1)处的切线方程为( )
A.x-y=0 B.x+y-2=0
C.x+4y-5=0 D.x-4y-5=0
[答案] A利用导数求参数 [解析] ∵f(x)的图象过点P(0,1),∴e=1.
又∵f(x)为偶函数,∴f(-x)=f(x).
故ax4+bx3+cx2+dx+e=ax4-bx3+cx2-dx+e.
∴b=0,d=0.∴f(x)=ax4+cx2+1.[方法规律总结] 1.导数的应用中,求导数是一个基本解题环节,应仔细分析函数解析式的结构特征,根据导数公式及运算法则求导数,不具备导数运算法则的结构形式时,先恒等变形,然后分析题目特点,探寻条件与结论的联系,选择解题途径.
2.求参数的问题一般依据条件建立参数的方程求解.已知抛物线y=ax2+bx-7通过点(1,1),过点(1,1)的切线方程为4x-y-3=0,求a、b的值.
[解析] 由于抛物线y=ax2+bx-7经过点(1,1),
∴1=a+b-7,即a+b-8=0 ①
又由于经过点(1,1)的抛物线的切线方程为
4x-y-3=0,
∴经过该点的抛物线的切线斜率为4.
∵y′=(ax2+bx-7)′=2ax+b,∴2a+b-4=0. ②
由①、②解得a=-4,b=12.[辨析] 这是复合函数的导数,但复合函数的导数我们没有学习讨论过,遇到这种类型的函数求导,可先整理,再求导.
函数y=sin2x的导数为( )
A.y′=cos2x B.y′=2cos2x
C.y′=2(sin2x-cos2x) D.y′=-sin2x
[答案] B
[解析] y′=(sin2x)′=(2sinxcosx)′
=2(sinx)′·cosx+2sinx(cosx)′
=2cos2x-2sin2x=2cos2x.
