3.3.2 函数的极值与导数 课件3
文档属性
| 名称 | 3.3.2 函数的极值与导数 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 82.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览




文档简介
课件11张PPT。3.3.2函数的极值与导数 已知函数 f(x)=2x3-6x2+7
(1)求f(x)的单调区间,并画出其图象;【复习与思考】(2)函数f(x)在x=0和x=2处的函数值与这两点附近的函数值有什么关系? 设函数y=f(x)在x=x0及其附近有定义,
(1)如果在x=x0处的函数值比它附近所有各点的函数值都大,即f(x)y=f(x)的一个极大值.记作:y极大值=f(x0)【函数极值的定义】(2)如果在x=x0处的函数值比它附近所有各点的函数值都小,即f(x)>f(x0),则称 f(x0)是函数
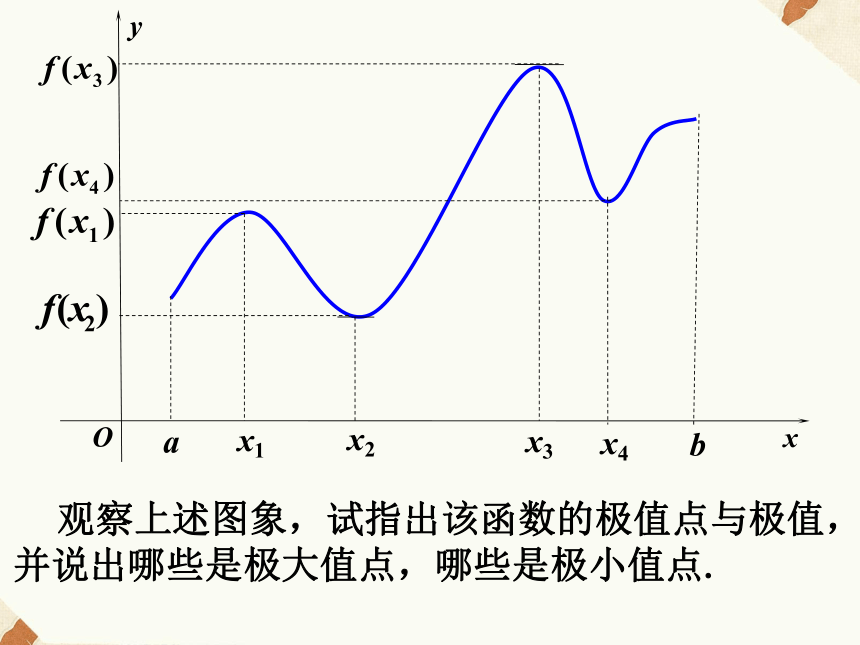
y=f(x)的一个极小值.记作:y极小值=f(x0)极大值与极小值统称为极值,x0叫做函数的极值点. 观察上述图象,试指出该函数的极值点与极值,并说出哪些是极大值点,哪些是极小值点.(1)极值是一个局部概念,反映了函数在某一点附近的大小情况;(2)极值点是自变量的值,极值指的是函数值;(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;【关于极值概念的几点说明】(4)函数的极值点一定在区间的内部,区间的端点不能成为极值点。而函数的最值既可能在区间的内部取得,也可能在区间的端点取得。【问题探究】 函数y=f(x)在极值点的导数值为多少?在极值点附近的导数符号有什么规律?(1)如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)>0
右侧f /(x0)<0, 那么f(x0)是极大值【函数的极值与导数的关系】(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)<0
右侧f /(x0)>0, 那么f(x0)是极小值(1) 求导数f/(x);
(2) 解方程 f/(x)=0
(3) 通过列表检查f/(x)在方程f/(x)=0的根的左右两侧的符号,进而确定函数的极值点与极值.【求函数极值的步骤】例题: 求函数
的极值. 【课堂练习】课本P96例2:求函数 的极值.【思考交流】导数值为0的点一定是函数的极值点吗? 对于可导函数而言,其极值点一定是导数为0的点,反之导数为0的点不一定是函数的极值点.因此:导数值为0的点是该点为极值点的必要非充分条件.
(1)求f(x)的单调区间,并画出其图象;【复习与思考】(2)函数f(x)在x=0和x=2处的函数值与这两点附近的函数值有什么关系? 设函数y=f(x)在x=x0及其附近有定义,
(1)如果在x=x0处的函数值比它附近所有各点的函数值都大,即f(x)
y=f(x)的一个极小值.记作:y极小值=f(x0)极大值与极小值统称为极值,x0叫做函数的极值点. 观察上述图象,试指出该函数的极值点与极值,并说出哪些是极大值点,哪些是极小值点.(1)极值是一个局部概念,反映了函数在某一点附近的大小情况;(2)极值点是自变量的值,极值指的是函数值;(3)函数的极大(小)值可能不止一个,而且函数的极大值未必大于极小值;【关于极值概念的几点说明】(4)函数的极值点一定在区间的内部,区间的端点不能成为极值点。而函数的最值既可能在区间的内部取得,也可能在区间的端点取得。【问题探究】 函数y=f(x)在极值点的导数值为多少?在极值点附近的导数符号有什么规律?(1)如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)>0
右侧f /(x0)<0, 那么f(x0)是极大值【函数的极值与导数的关系】(2)如果f /(x0)=0, 并且在x0附近的左侧 f /(x0)<0
右侧f /(x0)>0, 那么f(x0)是极小值(1) 求导数f/(x);
(2) 解方程 f/(x)=0
(3) 通过列表检查f/(x)在方程f/(x)=0的根的左右两侧的符号,进而确定函数的极值点与极值.【求函数极值的步骤】例题: 求函数
的极值. 【课堂练习】课本P96例2:求函数 的极值.【思考交流】导数值为0的点一定是函数的极值点吗? 对于可导函数而言,其极值点一定是导数为0的点,反之导数为0的点不一定是函数的极值点.因此:导数值为0的点是该点为极值点的必要非充分条件.
