3.3.3 函数的最大(小)值与导数 学案(无答案)
文档属性
| 名称 | 3.3.3 函数的最大(小)值与导数 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-10 00:00:00 | ||
图片预览

文档简介
3.3.3
函数的最大(小)值与导数
学案
【学习目标】
⒈理解函数的最大值和最小值的概念;
⒉掌握用导数求函数最值的方法和步骤
【重点难点】
导数求函数最值的方法和步骤
【学习内容】
一、课前准备
复习1:若满足,且在的两侧的导数异号,则是的极值点,是极值,并且如果在两侧满足“左正右负”,则是的________________点,是极_______值;如果在两侧满足“左负右正”,则是的_______点,是极_______值.
复习2:已知函数在时取得极值,且,(1)试求常数a、b、c的值;(2)试判断时函数有极大值还是极小值,并说明理由.
二、新课导学
※
学习探究
探究任务一:函数的最大(小)值
问题:观察在闭区间上的函数的图象,你能找出它的极大(小)值吗?最大值,最小值呢?
在图1中,在闭区间上的最大值是_______,最小值是_______;
在图2中,在闭区间上的极大值是_______,极小值是_______;最大值是_______,最小值是_______.
新知:一般地,在闭区间上连续的函数在上必有最大值与最小值.
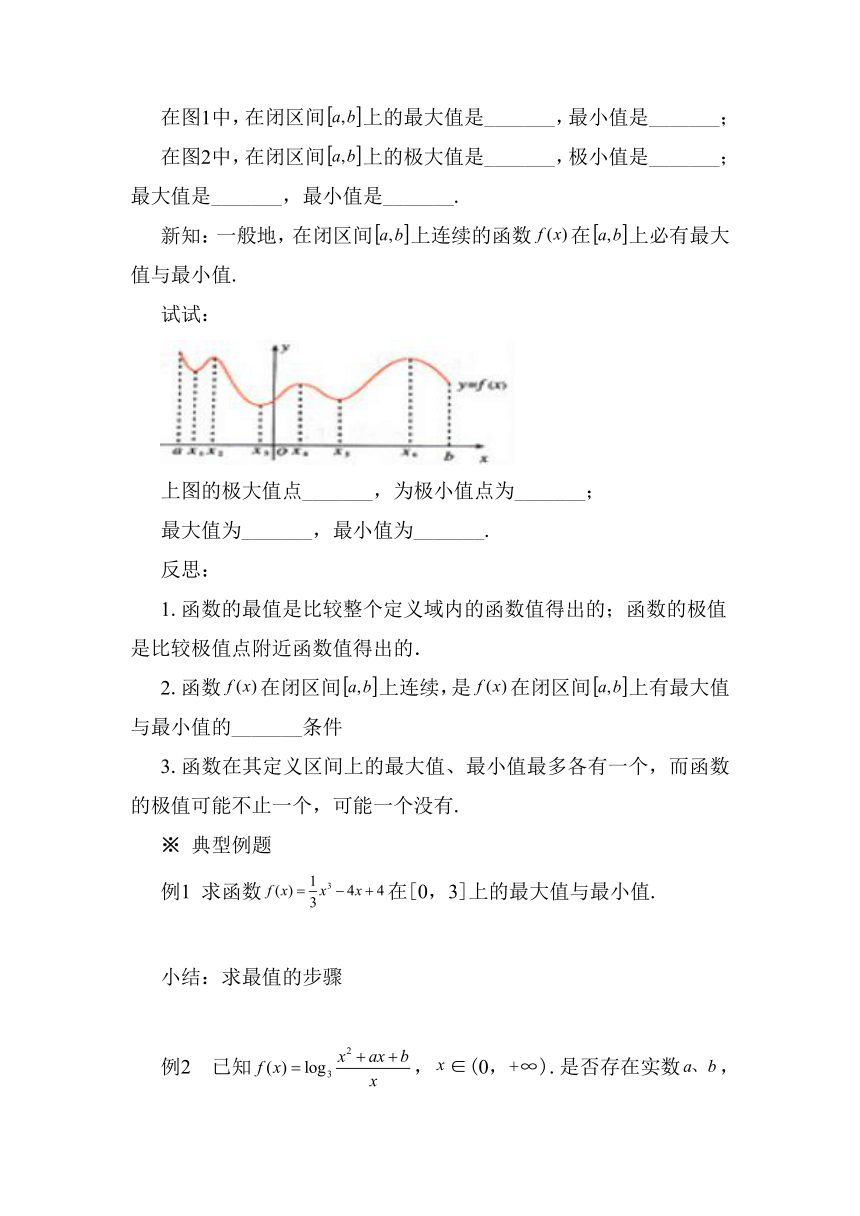
试试:
上图的极大值点_______,为极小值点为_______;
最大值为_______,最小值为_______.
反思:
1.函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的.
2.函数在闭区间上连续,是在闭区间上有最大值与最小值的_______条件
3.函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,可能一个没有.
※
典型例题
例1
求函数在[0,3]上的最大值与最小值.
小结:求最值的步骤
例2
已知,∈(0,+∞).是否存在实数,使同时满足下列两个条件:(1)在上是减函数,在上是增函数;(2)的最小值是1;
若存在,求出,若不存在,说明理由.
变式:设,函数在区间上的最大值为1,最小值为,求函数的解析式.
小结:本题属于逆向探究题型.解这类问题的基本方法是待定系数法,从逆向思维出发,实现由已知向未知的转化,转化过程中通过列表,直观形象,最终落脚在比较极值点与端点值大小上,从而解决问题.
练1.求函数的最值.
练2.
已知函数在上有最小值.(1)求实数的值;(2)求在上的最大值.
三、总结提升
※
学习小结
设函数在上连续,在内可导,则求在上的最大值与最小值的步骤如下:
⑴求在内的极值;
⑵将的各极值与、比较得出函数在上的最值.
四、课后作业
1.若函数在区间上的最大值、最小值分别为M、N,则的值为(
)
A.2
B.4
C.18
D.20
2.函数(
)
A.有最大值但无最小值
B.有最大值也有最小值
C.无最大值也无最小值
D.无最大值但有最小值
3.
已知函数在区间上的最大值为,则等于(
)
A.
B.
C.
D.或
4.
函数在上的最大值为_______.
5.
已知(为常数)在上有最大值,那么此函数在上的最小值是_______.
6.
为常数,求函数的最大值.
7.
已知函数,(1)求的单调区间;(2)若在区间上的最大值为20,求它在该区间上的最小值.
图2
图1
函数的最大(小)值与导数
学案
【学习目标】
⒈理解函数的最大值和最小值的概念;
⒉掌握用导数求函数最值的方法和步骤
【重点难点】
导数求函数最值的方法和步骤
【学习内容】
一、课前准备
复习1:若满足,且在的两侧的导数异号,则是的极值点,是极值,并且如果在两侧满足“左正右负”,则是的________________点,是极_______值;如果在两侧满足“左负右正”,则是的_______点,是极_______值.
复习2:已知函数在时取得极值,且,(1)试求常数a、b、c的值;(2)试判断时函数有极大值还是极小值,并说明理由.
二、新课导学
※
学习探究
探究任务一:函数的最大(小)值
问题:观察在闭区间上的函数的图象,你能找出它的极大(小)值吗?最大值,最小值呢?
在图1中,在闭区间上的最大值是_______,最小值是_______;
在图2中,在闭区间上的极大值是_______,极小值是_______;最大值是_______,最小值是_______.
新知:一般地,在闭区间上连续的函数在上必有最大值与最小值.
试试:
上图的极大值点_______,为极小值点为_______;
最大值为_______,最小值为_______.
反思:
1.函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的.
2.函数在闭区间上连续,是在闭区间上有最大值与最小值的_______条件
3.函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,可能一个没有.
※
典型例题
例1
求函数在[0,3]上的最大值与最小值.
小结:求最值的步骤
例2
已知,∈(0,+∞).是否存在实数,使同时满足下列两个条件:(1)在上是减函数,在上是增函数;(2)的最小值是1;
若存在,求出,若不存在,说明理由.
变式:设,函数在区间上的最大值为1,最小值为,求函数的解析式.
小结:本题属于逆向探究题型.解这类问题的基本方法是待定系数法,从逆向思维出发,实现由已知向未知的转化,转化过程中通过列表,直观形象,最终落脚在比较极值点与端点值大小上,从而解决问题.
练1.求函数的最值.
练2.
已知函数在上有最小值.(1)求实数的值;(2)求在上的最大值.
三、总结提升
※
学习小结
设函数在上连续,在内可导,则求在上的最大值与最小值的步骤如下:
⑴求在内的极值;
⑵将的各极值与、比较得出函数在上的最值.
四、课后作业
1.若函数在区间上的最大值、最小值分别为M、N,则的值为(
)
A.2
B.4
C.18
D.20
2.函数(
)
A.有最大值但无最小值
B.有最大值也有最小值
C.无最大值也无最小值
D.无最大值但有最小值
3.
已知函数在区间上的最大值为,则等于(
)
A.
B.
C.
D.或
4.
函数在上的最大值为_______.
5.
已知(为常数)在上有最大值,那么此函数在上的最小值是_______.
6.
为常数,求函数的最大值.
7.
已知函数,(1)求的单调区间;(2)若在区间上的最大值为20,求它在该区间上的最小值.
图2
图1
