人教版九年级上册21.1一元二次方程同步教学课件
文档属性
| 名称 | 人教版九年级上册21.1一元二次方程同步教学课件 |  | |
| 格式 | zip | ||
| 文件大小 | 128.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 14:26:04 | ||
图片预览






文档简介
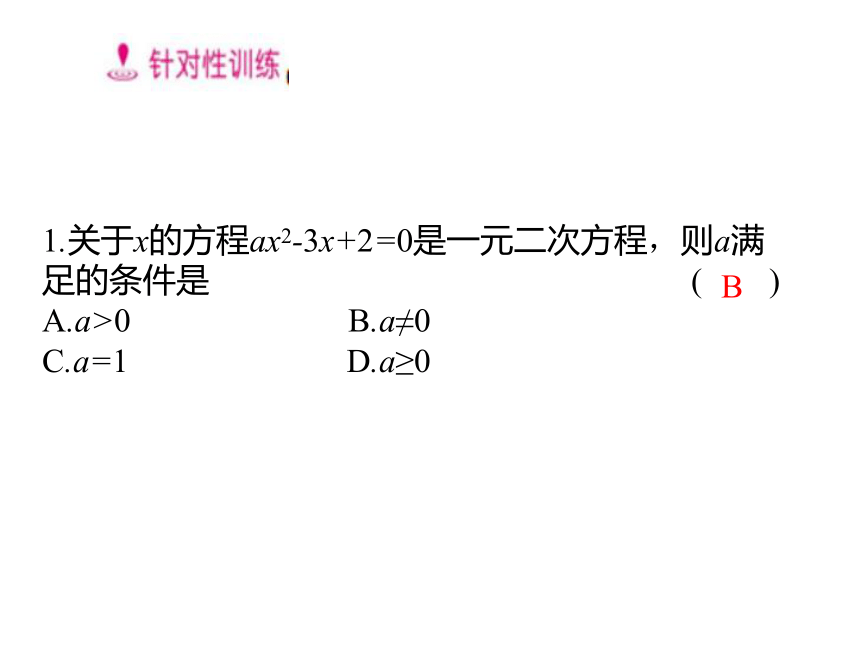
课件15张PPT。第二十一章 一元二次方程21.1 一元二次方程九年级数学·上 新课标 [人]应用一元二次方程的定义解决问题(2015·武汉北大附中模拟)已知(m-2)x2-3x+1=0是关于x的一元二次方程,则m的取值范围是 .?〔解析〕 根据题意得m-2≠0,所以m≠2.故填m≠2.m≠2考查角度1 应用一元二次方程的概念求字 母的取值范围1.关于x的方程ax2-3x+2=0是一元二次方程,则a满足的条件是 ( )
A.a>0 B.a≠0
C.a=1 D.a≥0B考查角度2 应用一元二次方程的概念求字母的值(2015·泗洪育才中学模拟)若方程(m+3)x|m|-1
+3mx=0是关于x的一元二次方程,则m= .?〔解析〕∵(m+3)x|m|-1+3mx=0是关于x的一元二次方程,∴m+3≠0,|m|-1=2,解得m=3.3 2. (2015·龙口期中)方程(m+2)x|m|+mx-8=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠±2[提示:由(m+2)x|m|+mx-8=0是关于x的一元二次方程,得 解得m=2.]B(探究题)当k为何值时,关于x的方程(k2-1)x2-(k+1)x-4=0:
(1)是一元二次方程? (2)是一元一次方程?〔解析〕若方程为一元二次方程,则二次项系数不为零,即化为一般形式为ax2+bx+c=0(a≠0);若方程为一元一次方程,则二次项系数为零,且一次项系数不为零,即化为一般形式为ax+b=0(a≠0).解:(1)∵(k2-1)x2-(k+1)x-4=0是一元二次方程,∴k2-1≠0,即k≠±1,∴k≠±1时,原方程是一元二次方程.(2)∵(k2-1)x2-(k+1)x-4=0是一元一次方程,即k=1,∴k=1时,原方程是一元一次方程.【解题归纳】 本题主要考查了一元二次方程和一元一次方程的定义,关键是注意一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;②只含有一个未知数;③未知数的最高次数是2.(1)若方程是一元二次方程,求m的值;
(2)若方程是一元一次方程,则m是否存在?若存在,请写出m的
值,并把方程解出来.
3.已知关于x的 方程, 回答下列问题.解:(1)由题意得 解得m=-1.(2)①当m-1≠0时,有则方程变为-3x-1=0,解得x= .②当m=1时,方程是一元一次方程,方程变为-x-1=0,解得x=-1. 解得m=0,应用一元二次方程的解的定义解决问题考查角度1 整体代入求字母或代数式的值(2015·重庆八中一模)若m是关于x的方程ax2+bx+5=0的一个解,则am2+bm-7等于 ( )
A.-2 B.1 C.-12 D.12〔解析〕 把x=m代入ax2+bx+5=0,得am2+bm+5
=0,则am2+bm=-5,所以am2+bm-7=-5-7=-12.C【解题归纳】 整体代入法是代数式求值的常用方法之一,在代数式的求值过程中,有时不需要将具体未知数的值代入,而是直接将某一个整体代入所求式,即可得解.4.(2015·盐城模拟)若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则a+b+2015的值是 .?[提示:∵关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,∴a+b+5=0,则a+b=-5,∴a+b+2015=-5+2015=2010.] 2010考查角度2 利用因式分解求字母或代数式的值〔解析〕 ∵x=-1是一元二次方程ax2+bx-10=0的一个解,
∴a-b-10=0,∴a-b=10.∵a≠-b,∴a+b≠0,
(2015·泰州模拟)已知x=-1是一元二次方程ax2+bx-10=0的一个解,且a≠-b,则 的值为 .?55.若c(c≠0)为关于x的一元二次方程x2+bx+c=0的根,则c+b的值为 ( )
A.1 B.-1 C.2 D.-2[提示:把x=c代入x2+bx+c=0,得c2+bc+c=0,即c(c+b+1)=0.∵c≠0,∴c+b+1=0,即c+b= -1.]B (2015·北京期中)已知a是方程x2+5x-2=0的一个根,则代数式2a2+10a-7的值为 ;代数式a3+6a2+3a+4的值为 .?〔解析〕∵a是方程x2+5x-2=0的一个根,∴x=a满
足该方程,∴a2+5a-2=0,即a2+5a=2,∴2a2+10a-7
=2(a2+5a)-7=4-7=-3;a3+6a2+3a+4=a(a2+5a)+a2+3a+4=a2+5a+4=2+4=6. 6-3 6.(2015·扬州模拟)已知m是方程x2-x-3=0的一个实数根,则代数式(m2-m)· 的值为 .?6=1, [提示:∵m是方程x2-x-3=0的一个实数根,∴m2-m-3=0,∴m2-m=3,m2-3=m,由题意知m≠0,∴实际问题中的一元二次方程模型 某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为 ( )
A.x(x-11)=180 B.2x+2(x-11)=180
C.x(x+11)=180 D.2x+2(x+11)=180〔解析〕 若宽为x米,则长为(x+11)米,根据题意得x(x+11)=180.【解题归纳】 本题考查了一元二次方程的应用,解题的关键是根据矩形的面积公式列出方程.C 7.某初中毕业班的每一位同学都将自己的照片向全班其他同学各送一张表示留念,全班共送了2550张相片,如果全班有x名学生,根据题意可列出方程为( )
A.x(x+1)=2550 B.x(x-1)=2550
C.2x(x-1)=2550 D.x(x-1)=2550×2[提示:∵全班有x名学生,∴每名学生应该送的相片为(x-1)张,∴x(x-1)=2550.]B
A.a>0 B.a≠0
C.a=1 D.a≥0B考查角度2 应用一元二次方程的概念求字母的值(2015·泗洪育才中学模拟)若方程(m+3)x|m|-1
+3mx=0是关于x的一元二次方程,则m= .?〔解析〕∵(m+3)x|m|-1+3mx=0是关于x的一元二次方程,∴m+3≠0,|m|-1=2,解得m=3.3 2. (2015·龙口期中)方程(m+2)x|m|+mx-8=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠±2[提示:由(m+2)x|m|+mx-8=0是关于x的一元二次方程,得 解得m=2.]B(探究题)当k为何值时,关于x的方程(k2-1)x2-(k+1)x-4=0:
(1)是一元二次方程? (2)是一元一次方程?〔解析〕若方程为一元二次方程,则二次项系数不为零,即化为一般形式为ax2+bx+c=0(a≠0);若方程为一元一次方程,则二次项系数为零,且一次项系数不为零,即化为一般形式为ax+b=0(a≠0).解:(1)∵(k2-1)x2-(k+1)x-4=0是一元二次方程,∴k2-1≠0,即k≠±1,∴k≠±1时,原方程是一元二次方程.(2)∵(k2-1)x2-(k+1)x-4=0是一元一次方程,即k=1,∴k=1时,原方程是一元一次方程.【解题归纳】 本题主要考查了一元二次方程和一元一次方程的定义,关键是注意一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;②只含有一个未知数;③未知数的最高次数是2.(1)若方程是一元二次方程,求m的值;
(2)若方程是一元一次方程,则m是否存在?若存在,请写出m的
值,并把方程解出来.
3.已知关于x的 方程, 回答下列问题.解:(1)由题意得 解得m=-1.(2)①当m-1≠0时,有则方程变为-3x-1=0,解得x= .②当m=1时,方程是一元一次方程,方程变为-x-1=0,解得x=-1. 解得m=0,应用一元二次方程的解的定义解决问题考查角度1 整体代入求字母或代数式的值(2015·重庆八中一模)若m是关于x的方程ax2+bx+5=0的一个解,则am2+bm-7等于 ( )
A.-2 B.1 C.-12 D.12〔解析〕 把x=m代入ax2+bx+5=0,得am2+bm+5
=0,则am2+bm=-5,所以am2+bm-7=-5-7=-12.C【解题归纳】 整体代入法是代数式求值的常用方法之一,在代数式的求值过程中,有时不需要将具体未知数的值代入,而是直接将某一个整体代入所求式,即可得解.4.(2015·盐城模拟)若关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,则a+b+2015的值是 .?[提示:∵关于x的一元二次方程ax2+bx+5=0(a≠0)的一个解是x=1,∴a+b+5=0,则a+b=-5,∴a+b+2015=-5+2015=2010.] 2010考查角度2 利用因式分解求字母或代数式的值〔解析〕 ∵x=-1是一元二次方程ax2+bx-10=0的一个解,
∴a-b-10=0,∴a-b=10.∵a≠-b,∴a+b≠0,
(2015·泰州模拟)已知x=-1是一元二次方程ax2+bx-10=0的一个解,且a≠-b,则 的值为 .?55.若c(c≠0)为关于x的一元二次方程x2+bx+c=0的根,则c+b的值为 ( )
A.1 B.-1 C.2 D.-2[提示:把x=c代入x2+bx+c=0,得c2+bc+c=0,即c(c+b+1)=0.∵c≠0,∴c+b+1=0,即c+b= -1.]B (2015·北京期中)已知a是方程x2+5x-2=0的一个根,则代数式2a2+10a-7的值为 ;代数式a3+6a2+3a+4的值为 .?〔解析〕∵a是方程x2+5x-2=0的一个根,∴x=a满
足该方程,∴a2+5a-2=0,即a2+5a=2,∴2a2+10a-7
=2(a2+5a)-7=4-7=-3;a3+6a2+3a+4=a(a2+5a)+a2+3a+4=a2+5a+4=2+4=6. 6-3 6.(2015·扬州模拟)已知m是方程x2-x-3=0的一个实数根,则代数式(m2-m)· 的值为 .?6=1, [提示:∵m是方程x2-x-3=0的一个实数根,∴m2-m-3=0,∴m2-m=3,m2-3=m,由题意知m≠0,∴实际问题中的一元二次方程模型 某校准备修建一个面积为180平方米的矩形活动场地,它的长比宽多11米,设场地的宽为x米,则可列方程为 ( )
A.x(x-11)=180 B.2x+2(x-11)=180
C.x(x+11)=180 D.2x+2(x+11)=180〔解析〕 若宽为x米,则长为(x+11)米,根据题意得x(x+11)=180.【解题归纳】 本题考查了一元二次方程的应用,解题的关键是根据矩形的面积公式列出方程.C 7.某初中毕业班的每一位同学都将自己的照片向全班其他同学各送一张表示留念,全班共送了2550张相片,如果全班有x名学生,根据题意可列出方程为( )
A.x(x+1)=2550 B.x(x-1)=2550
C.2x(x-1)=2550 D.x(x-1)=2550×2[提示:∵全班有x名学生,∴每名学生应该送的相片为(x-1)张,∴x(x-1)=2550.]B
同课章节目录
