天津市宁河县造甲城中学教学资料-24.1.2垂径定理(说课)
文档属性
| 名称 | 天津市宁河县造甲城中学教学资料-24.1.2垂径定理(说课) |

|
|
| 格式 | zip | ||
| 文件大小 | 76.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 00:00:00 | ||
图片预览




文档简介
课件14张PPT。第24章 圆《垂径定理》说课
新课标人教版数学教材 九年级下册从教材分析,教法设计,学法指导,教学程序,设计说明
教学反思,六个方面对本课的设计进行说明。
教材分析
1、教材所处的地位以及前后联系:
这节课的主要内容是垂径定理及其推论,它们是在学生学习 轴对称图形及其性质等知识的基础上学习的,是本章的重点内容之一,也是在中考中常常用到的定理。这个定理提供了证明两条线段相等,两条孤相等,垂直和证明直径的方法。因此,学好本节课的知识尤为重要。可以说这节课无论在知识上,还是在学生能力培养上,都起着十分重要的作用。
2、教学目标:
1)、知识目标:
A、理解掌握圆是一个轴对称图形。
B、在清晰垂径定理的题设与结论的基础上,熟记垂径定
理及其两个推论。
2)、能力目标:能够在有关几何证明与计算中熟练应用垂径定
理及其推论。
3)、思想教育目标: 通过对垂径定理及其逆定理的推导分析,培
养学生的逆向思维,发散思维。
4)、身心素质目标:激励全体学生增强学好数学的信心,培养
不怕困难,勇于进取,大胆探索的良好的心理素质。
3、重点、难点和关键
根据新课标的要求和本节内容的目标,确定本节课的 重点:垂径定理及其两个推论的推导及应用。
难点:怎样把这个定理在具体的几何题目中灵活应用。
问题的关键:熟记定理的五个方面
①过圆心;
②垂直于弦;
③平分弦;
④平分弦所对的优弧;
⑤平分弦所对的劣弧.每满足两个方面,就有另外的三个方面教学说明
1、教法设计:
1)本节课采用引导发现法,自主,探究,合作,交流 讨论法,讲练结合法。
2)采用多媒体课件,投影仪等现代化教学手段,增大教 学容量和增强直观性。
2、学法指导:
1)为了培养学生动手,动脑,动口能力,这节课采用制 作学具,动手实验,自己发现结论,总结规律的学习 方法,让学生进行创造性学习。
2)结合教材,借助直观教具,图形,重点使用“数形结 合”, “转化”的数学思想。
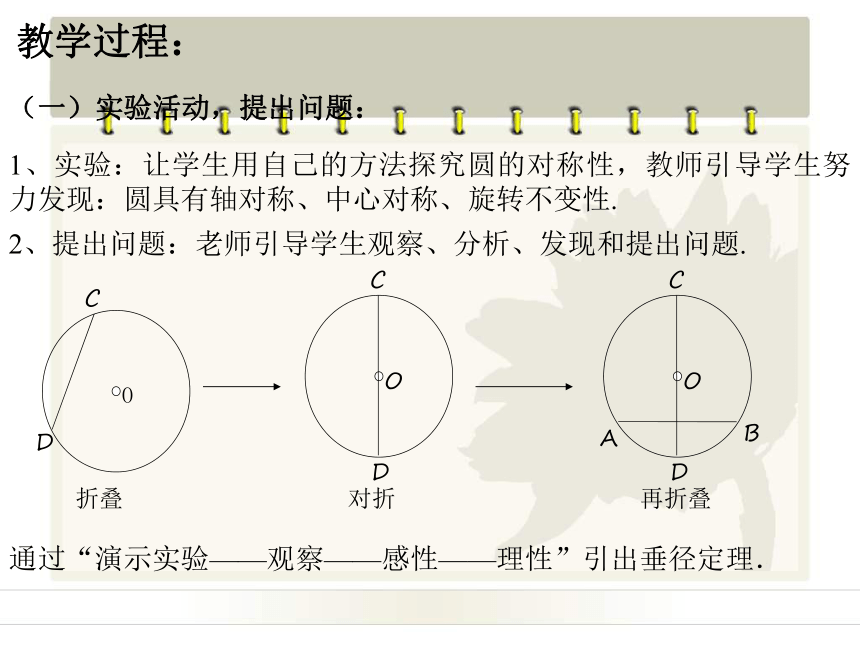
3)鼓励学生多角度思维问题,逆向思维问题,把学习与 创造结合起来,创造才能的发挥是学生主体作用的最 高体现。教学过程:(一)实验活动,提出问题: 1、实验:让学生用自己的方法探究圆的对称性,教师引导学生努力发现:圆具有轴对称、中心对称、旋转不变性.
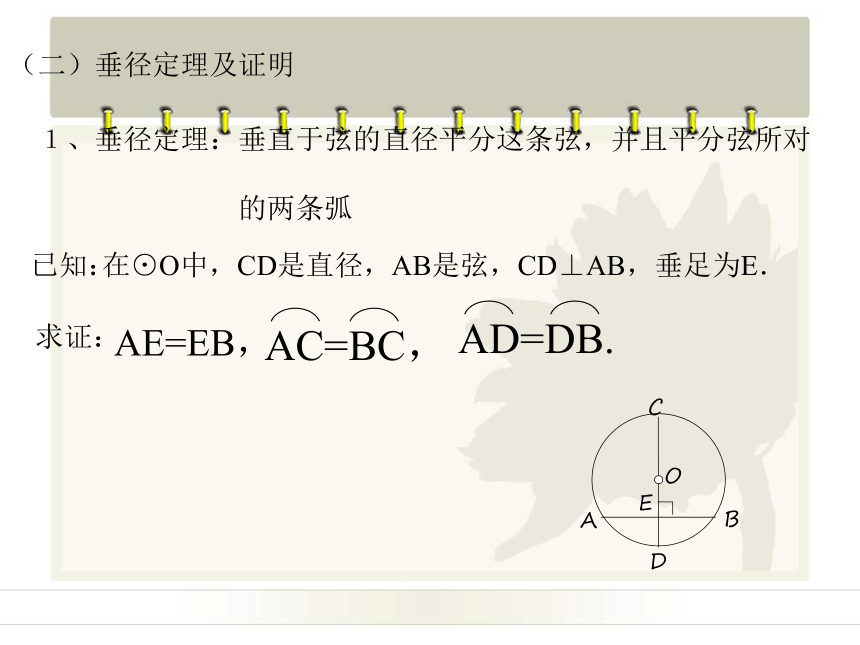
2、提出问题:老师引导学生观察、分析、发现和提出问题. O通过“演示实验——观察——感性——理性”引出垂径定理. (二)垂径定理及证明AC=BC,AD=DB.求证:AE=EB, 1、垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对
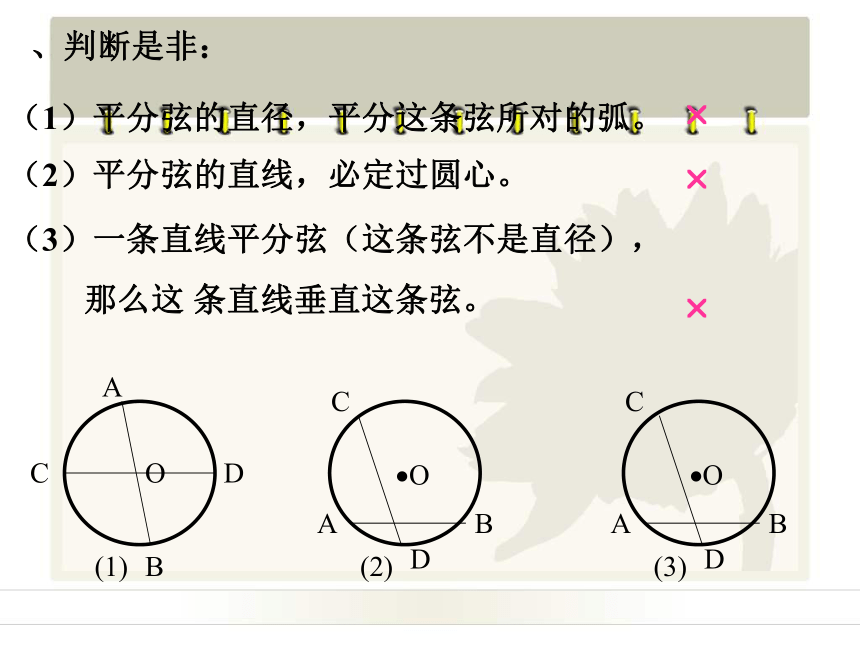
的两条弧 、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???(7)平分弦的直径垂直于弦?填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若_____________________________________________________,则CE=DE(只需填写一个你认为适当的条件)
2、如图:已知AB是⊙O的弦,OB=4cm,∠ABO=300,则O到AB的距离是___________cm,AB=_________cm.第1题图第2题图24H选择:
如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2 C、1 D、0A1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.活 动 三在Rt△AOE中2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.∴∵ OE⊥AC OD⊥AB(1)巩固新知识,通过作业反馈教学不足
(2)强化基本技能训练,培养学生良好习惯和品质。
(3)分两种层次,既利于面向全体,又利于分类推进,因材施教。
几点说明:
1、板书设计:(1)教师板书定理、证明定理(2)分析定理、得出推论(3)典例(4)典练、学生板演
2、时间的大体安排:情境导入约5分钟,定理的证明、分析、推论的导出约15分钟,典例约8分钟,典型训练7分钟,随堂测试7分钟,小结作业约3分钟。
3、整个设计要突出体现的特色:
〈1〉面向全体学生,因材施教,选择恰当的教学方法及适当的教学起点。
〈2〉加强知识的发生,发展及形成过程,充分展示学生的思维过程,重视能力的培养。
〈3〉充分体现“数学教学是数学活动的教学”的思想,发挥学生的主体参与作用。
教学反思学生为主体体现的不够充分。
由于时间检测未完成
学生练习的实践比较充裕,学生板演,较果较好。
新课标人教版数学教材 九年级下册从教材分析,教法设计,学法指导,教学程序,设计说明
教学反思,六个方面对本课的设计进行说明。
教材分析
1、教材所处的地位以及前后联系:
这节课的主要内容是垂径定理及其推论,它们是在学生学习 轴对称图形及其性质等知识的基础上学习的,是本章的重点内容之一,也是在中考中常常用到的定理。这个定理提供了证明两条线段相等,两条孤相等,垂直和证明直径的方法。因此,学好本节课的知识尤为重要。可以说这节课无论在知识上,还是在学生能力培养上,都起着十分重要的作用。
2、教学目标:
1)、知识目标:
A、理解掌握圆是一个轴对称图形。
B、在清晰垂径定理的题设与结论的基础上,熟记垂径定
理及其两个推论。
2)、能力目标:能够在有关几何证明与计算中熟练应用垂径定
理及其推论。
3)、思想教育目标: 通过对垂径定理及其逆定理的推导分析,培
养学生的逆向思维,发散思维。
4)、身心素质目标:激励全体学生增强学好数学的信心,培养
不怕困难,勇于进取,大胆探索的良好的心理素质。
3、重点、难点和关键
根据新课标的要求和本节内容的目标,确定本节课的 重点:垂径定理及其两个推论的推导及应用。
难点:怎样把这个定理在具体的几何题目中灵活应用。
问题的关键:熟记定理的五个方面
①过圆心;
②垂直于弦;
③平分弦;
④平分弦所对的优弧;
⑤平分弦所对的劣弧.每满足两个方面,就有另外的三个方面教学说明
1、教法设计:
1)本节课采用引导发现法,自主,探究,合作,交流 讨论法,讲练结合法。
2)采用多媒体课件,投影仪等现代化教学手段,增大教 学容量和增强直观性。
2、学法指导:
1)为了培养学生动手,动脑,动口能力,这节课采用制 作学具,动手实验,自己发现结论,总结规律的学习 方法,让学生进行创造性学习。
2)结合教材,借助直观教具,图形,重点使用“数形结 合”, “转化”的数学思想。
3)鼓励学生多角度思维问题,逆向思维问题,把学习与 创造结合起来,创造才能的发挥是学生主体作用的最 高体现。教学过程:(一)实验活动,提出问题: 1、实验:让学生用自己的方法探究圆的对称性,教师引导学生努力发现:圆具有轴对称、中心对称、旋转不变性.
2、提出问题:老师引导学生观察、分析、发现和提出问题. O通过“演示实验——观察——感性——理性”引出垂径定理. (二)垂径定理及证明AC=BC,AD=DB.求证:AE=EB, 1、垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对
的两条弧 、判断是非:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),
那么这 条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的 弦。(6)弦垂直于直径,这条直径就被弦平分。???(7)平分弦的直径垂直于弦?填空:
1、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若_____________________________________________________,则CE=DE(只需填写一个你认为适当的条件)
2、如图:已知AB是⊙O的弦,OB=4cm,∠ABO=300,则O到AB的距离是___________cm,AB=_________cm.第1题图第2题图24H选择:
如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2 C、1 D、0A1.如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.·OABE练习解:答:⊙O的半径为5cm.活 动 三在Rt△AOE中2.如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.证明:∴四边形ADOE为矩形,又 ∵AC=AB∴ AE=AD∴ 四边形ADOE为正方形.∴∵ OE⊥AC OD⊥AB(1)巩固新知识,通过作业反馈教学不足
(2)强化基本技能训练,培养学生良好习惯和品质。
(3)分两种层次,既利于面向全体,又利于分类推进,因材施教。
几点说明:
1、板书设计:(1)教师板书定理、证明定理(2)分析定理、得出推论(3)典例(4)典练、学生板演
2、时间的大体安排:情境导入约5分钟,定理的证明、分析、推论的导出约15分钟,典例约8分钟,典型训练7分钟,随堂测试7分钟,小结作业约3分钟。
3、整个设计要突出体现的特色:
〈1〉面向全体学生,因材施教,选择恰当的教学方法及适当的教学起点。
〈2〉加强知识的发生,发展及形成过程,充分展示学生的思维过程,重视能力的培养。
〈3〉充分体现“数学教学是数学活动的教学”的思想,发挥学生的主体参与作用。
教学反思学生为主体体现的不够充分。
由于时间检测未完成
学生练习的实践比较充裕,学生板演,较果较好。
同课章节目录
