平行四边形练习题(含答案)
图片预览


文档简介
平行四边形练习题(含答案)
一.选择题(共10小题)
1.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,②
B.①,④
C.③,④
D.②,③
(1题图)
(2题图)
(3题图)
2.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.12
B.13
C.14
D.15
3.如图,在△ABC中,E是AB的中点,AF交BC于F,CD平分∠ACB,且CD⊥AF,垂足为D,连接DE,若BC=12,AC=8,则DE的长为( )
A.2
B.2.5
C.3
D.4
4.若一个多边形的内角和与它的外角和相等,则这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
5.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米
B.150米
C.160米
D.240米
(5题图)
(8题图)
(9题图)
6.过多边形的一个顶点的所有对角线把多边形分成4个三角形,这个多边形对角线的总条数是( )
A.8
B.9
C.10
D.11
7.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
8.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
10.如图,已知四边形ABCD,对角线AC和BD相交于O,下面选项不能得出四边形ABCD是平行四边形的是( )
A.AB∥CD,且AB=CD
B.AB=CD,AD=BC
C.AO=CO,BO=DO
D.AB∥CD,且AD=BC
(10题图)
(11题图)
(12题图)
二.填空题(共7小题)
11.如图,E、F是 ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是: .
12.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是 .
13.如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为 .
(13题图)
(17题图)
14.从多边形的一个顶点出发引对角线,可以把这个多边形分割成6个三角形,则该多边形为 边形.
15.从四边形的一个顶点出发,可得一条对角线;从五边形的一个顶点出发可得二条对角线;从六边形的一个顶点出发可得三条对角线;…按此规律,从n(n≥4,且n是整数)边形的一个顶点出发可得对角线 条.
16.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
17.如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .
三.解答题(共10小题)
18.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
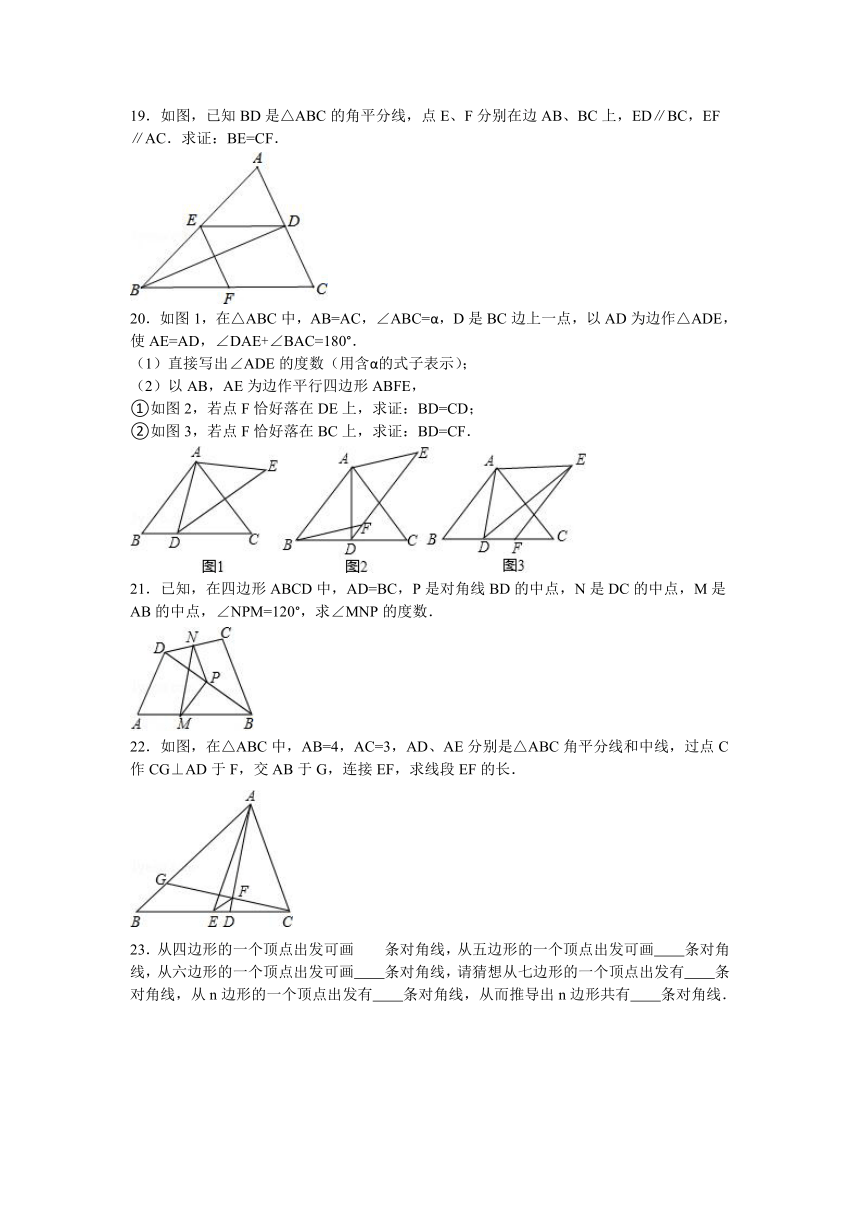
19.如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
20.如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.
(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
21.已知,在四边形ABCD中,AD=BC,P是对角线BD的中点,N是DC的中点,M是AB的中点,∠NPM=120°,求∠MNP的度数.
22.如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
23.从四边形的一个顶点出发可画 条对角线,从五边形的一个顶点出发可画 条对角线,从六边形的一个顶点出发可画 条对角线,请猜想从七边形的一个顶点出发有 条对角线,从n边形的一个顶点出发有 条对角线,从而推导出n边形共有 条对角线.
24.如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠A=120゜.求∠1+∠2+∠3+∠4的度数.
25.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
26.看图回答问题:
(1)内角和为2014°,小明为什么不说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
27.如图,在 ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
平行四边形练习题(含答案)
一.选择题(共10小题)
1.D.2.C. 3.A.4.B.5.B.6.B.7.C.8.D.9.D. 10.D.
二.填空题(共7小题)
11. BE=DF(答案不唯一); .12. 两组对边分别相等的四边形是平行四边形 .
13. 7 .14. 八 .15. (n﹣3) .16. 6 .17. 36° .
三.解答题(共10小题)
18.(解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,,∴△ABE≌△FCE(AAS);
∴AE=EF,又∵BE=CE∴四边形ABFC是平行四边形.
19.证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,
∵BD平分∠ABC,∴∠EBD=∠DBC,
∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,∴EB=CF.
20.解:(1)∵在△ABC中,AB=AC,∠ABC=α,∴∠BAC=180°﹣2α,
∵∠DAE+∠BAC=180°,∴∠DAE=2α,
∵AE=AD,∴∠ADE=90°﹣α;
(2)①证明:∵四边形ABFE是平行四边形,∴AB∥EF.∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°﹣α,∴∠ADC=∠ADE+∠EDC=90°,∴AD⊥BC.
∵AB=AC,∴BD=CD;
②证明:∵AB=AC,∠ABC=α,∴∠C=∠B=α.
∵四边形ABFE是平行四边形,∴AE∥BF,AE=BF.∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,∴∠DAC=α,∴∠DAC=∠C.∴AD=CD.
∵AD=AE=BF,∴BF=CD.∴BD=CF.
21.解:∵在四边形ABCD中,M、N、P分别是AB、CD、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AD,PN=CB,
∵AD=CB,∴PM=PN,∴△PMN是等腰三角形,∵∠NPM=120°,
∴∠MNP==30°.
22.解:在△AGF和△ACF中,,∴△AGF≌△ACF,
∴AG=AC=3,GF=CF,
则BG=AB﹣AG=4﹣3=1.
又∵BE=CE,
∴EF是△BCG的中位线,∴EF=BG=.
23.从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有条对角线,
故答案为:1;2;3;4;(n﹣3);.
24.解:∵与∠A相邻的外角的度数是:180﹣120=60°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300゜.
25.解:如图,连接BE,则∠1+∠2=∠D+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠E+∠F+∠G=(5﹣2)180°=540°.
26.解:(1)∵n边形的内角和是(n﹣2) 180°,
∴内角和一定是180度的倍数,
∵2014÷180=11…34,
∴内角和为2014°不可能;
(2)依题意有(x﹣2) 180°<2014°,解得x<13.
因而多边形的边数是13,故小华求的是十三边形的内角和;
(3)13边形的内角和是(13﹣2)×180°=1980°,2014°﹣1980°=34°,
因此这个外角的度数为34°.
27.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS).∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,∴AF=CE.
一.选择题(共10小题)
1.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.①,②
B.①,④
C.③,④
D.②,③
(1题图)
(2题图)
(3题图)
2.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( )
A.12
B.13
C.14
D.15
3.如图,在△ABC中,E是AB的中点,AF交BC于F,CD平分∠ACB,且CD⊥AF,垂足为D,连接DE,若BC=12,AC=8,则DE的长为( )
A.2
B.2.5
C.3
D.4
4.若一个多边形的内角和与它的外角和相等,则这个多边形是( )
A.三角形
B.四边形
C.五边形
D.六边形
5.如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是( )
A.140米
B.150米
C.160米
D.240米
(5题图)
(8题图)
(9题图)
6.过多边形的一个顶点的所有对角线把多边形分成4个三角形,这个多边形对角线的总条数是( )
A.8
B.9
C.10
D.11
7.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
A.7
B.10
C.35
D.70
8.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
A.OE=DC
B.OA=OC
C.∠BOE=∠OBA
D.∠OBE=∠OCE
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
10.如图,已知四边形ABCD,对角线AC和BD相交于O,下面选项不能得出四边形ABCD是平行四边形的是( )
A.AB∥CD,且AB=CD
B.AB=CD,AD=BC
C.AO=CO,BO=DO
D.AB∥CD,且AD=BC
(10题图)
(11题图)
(12题图)
二.填空题(共7小题)
11.如图,E、F是 ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是: .
12.如图,点D是直线l外一点,在l上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是 .
13.如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为 .
(13题图)
(17题图)
14.从多边形的一个顶点出发引对角线,可以把这个多边形分割成6个三角形,则该多边形为 边形.
15.从四边形的一个顶点出发,可得一条对角线;从五边形的一个顶点出发可得二条对角线;从六边形的一个顶点出发可得三条对角线;…按此规律,从n(n≥4,且n是整数)边形的一个顶点出发可得对角线 条.
16.一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
17.如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .
三.解答题(共10小题)
18.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
19.如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
20.如图1,在△ABC中,AB=AC,∠ABC=α,D是BC边上一点,以AD为边作△ADE,使AE=AD,∠DAE+∠BAC=180°.
(1)直接写出∠ADE的度数(用含α的式子表示);
(2)以AB,AE为边作平行四边形ABFE,
①如图2,若点F恰好落在DE上,求证:BD=CD;
②如图3,若点F恰好落在BC上,求证:BD=CF.
21.已知,在四边形ABCD中,AD=BC,P是对角线BD的中点,N是DC的中点,M是AB的中点,∠NPM=120°,求∠MNP的度数.
22.如图,在△ABC中,AB=4,AC=3,AD、AE分别是△ABC角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.
23.从四边形的一个顶点出发可画 条对角线,从五边形的一个顶点出发可画 条对角线,从六边形的一个顶点出发可画 条对角线,请猜想从七边形的一个顶点出发有 条对角线,从n边形的一个顶点出发有 条对角线,从而推导出n边形共有 条对角线.
24.如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角,若∠A=120゜.求∠1+∠2+∠3+∠4的度数.
25.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
26.看图回答问题:
(1)内角和为2014°,小明为什么不说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
27.如图,在 ABCD中,AE⊥BD于E,CF⊥BD于F,连接AF,CE.求证:AF=CE.
平行四边形练习题(含答案)
一.选择题(共10小题)
1.D.2.C. 3.A.4.B.5.B.6.B.7.C.8.D.9.D. 10.D.
二.填空题(共7小题)
11. BE=DF(答案不唯一); .12. 两组对边分别相等的四边形是平行四边形 .
13. 7 .14. 八 .15. (n﹣3) .16. 6 .17. 36° .
三.解答题(共10小题)
18.(解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,,∴△ABE≌△FCE(AAS);
∴AE=EF,又∵BE=CE∴四边形ABFC是平行四边形.
19.证明:∵ED∥BC,EF∥AC,∴四边形EFCD是平行四边形,∴DE=CF,
∵BD平分∠ABC,∴∠EBD=∠DBC,
∵DE∥BC,∴∠EDB=∠DBC,∴∠EBD=∠EDB,∴EB=ED,∴EB=CF.
20.解:(1)∵在△ABC中,AB=AC,∠ABC=α,∴∠BAC=180°﹣2α,
∵∠DAE+∠BAC=180°,∴∠DAE=2α,
∵AE=AD,∴∠ADE=90°﹣α;
(2)①证明:∵四边形ABFE是平行四边形,∴AB∥EF.∴∠EDC=∠ABC=α,
由(1)知,∠ADE=90°﹣α,∴∠ADC=∠ADE+∠EDC=90°,∴AD⊥BC.
∵AB=AC,∴BD=CD;
②证明:∵AB=AC,∠ABC=α,∴∠C=∠B=α.
∵四边形ABFE是平行四边形,∴AE∥BF,AE=BF.∴∠EAC=∠C=α,
由(1)知,∠DAE=2α,∴∠DAC=α,∴∠DAC=∠C.∴AD=CD.
∵AD=AE=BF,∴BF=CD.∴BD=CF.
21.解:∵在四边形ABCD中,M、N、P分别是AB、CD、BD的中点,
∴PN,PM分别是△CDB与△DAB的中位线,
∴PM=AD,PN=CB,
∵AD=CB,∴PM=PN,∴△PMN是等腰三角形,∵∠NPM=120°,
∴∠MNP==30°.
22.解:在△AGF和△ACF中,,∴△AGF≌△ACF,
∴AG=AC=3,GF=CF,
则BG=AB﹣AG=4﹣3=1.
又∵BE=CE,
∴EF是△BCG的中位线,∴EF=BG=.
23.从四边形的一个顶点出发可画1条对角线,从五边形的一个顶点出发可画2条对角线,从六边形的一个顶点出发可画3条对角线,请猜想从七边形的一个顶点出发有4条对角线,从n边形的一个顶点出发有(n﹣3)条对角线,从而推导出n边形共有条对角线,
故答案为:1;2;3;4;(n﹣3);.
24.解:∵与∠A相邻的外角的度数是:180﹣120=60°,
∴∠1+∠2+∠3+∠4=360°﹣60°=300゜.
25.解:如图,连接BE,则∠1+∠2=∠D+∠C,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠A+∠B+∠1+∠2+∠E+∠F+∠G=(5﹣2)180°=540°.
26.解:(1)∵n边形的内角和是(n﹣2) 180°,
∴内角和一定是180度的倍数,
∵2014÷180=11…34,
∴内角和为2014°不可能;
(2)依题意有(x﹣2) 180°<2014°,解得x<13.
因而多边形的边数是13,故小华求的是十三边形的内角和;
(3)13边形的内角和是(13﹣2)×180°=1980°,2014°﹣1980°=34°,
因此这个外角的度数为34°.
27.证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF.
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,AE∥CF,
在△ABE和△CDF中,,∴△ABE≌△CDF(AAS).∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,∴AF=CE.
