鲁教版九年级数学下册第5单元5.6-5.7对应练习题(含答案)
文档属性
| 名称 | 鲁教版九年级数学下册第5单元5.6-5.7对应练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 274.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 15:21:24 | ||
图片预览

文档简介
鲁教版九年级数学下册第5单元5.6-5.7对应练习题(含答案)
一.选择题(共9小题)
1.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离
B.相切
C.相交
D.无法确定
2.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交
B.相切
C.相离
D.不能确定
3.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70°
B.35°
C.20°
D.40°
(3题图)
(4题图)
(5题图)
(6题图)
4.如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为
( )
A.40°
B.50°
C.55°
D.60°
5.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的个数是( )
A.1
个
B.2个
C.3
个
D.4个
6.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )
A.
B.
C.
D.2
7.圆I是三角形ABC的内切圆,D,E,F为3个切点,若∠DEF=52°,则∠A的度数为( )
A.68°
B.52°
C.76°
D.38°
(7题图)
(8题图)
(9题图)
8.如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
9.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
二.填空题(共7小题)
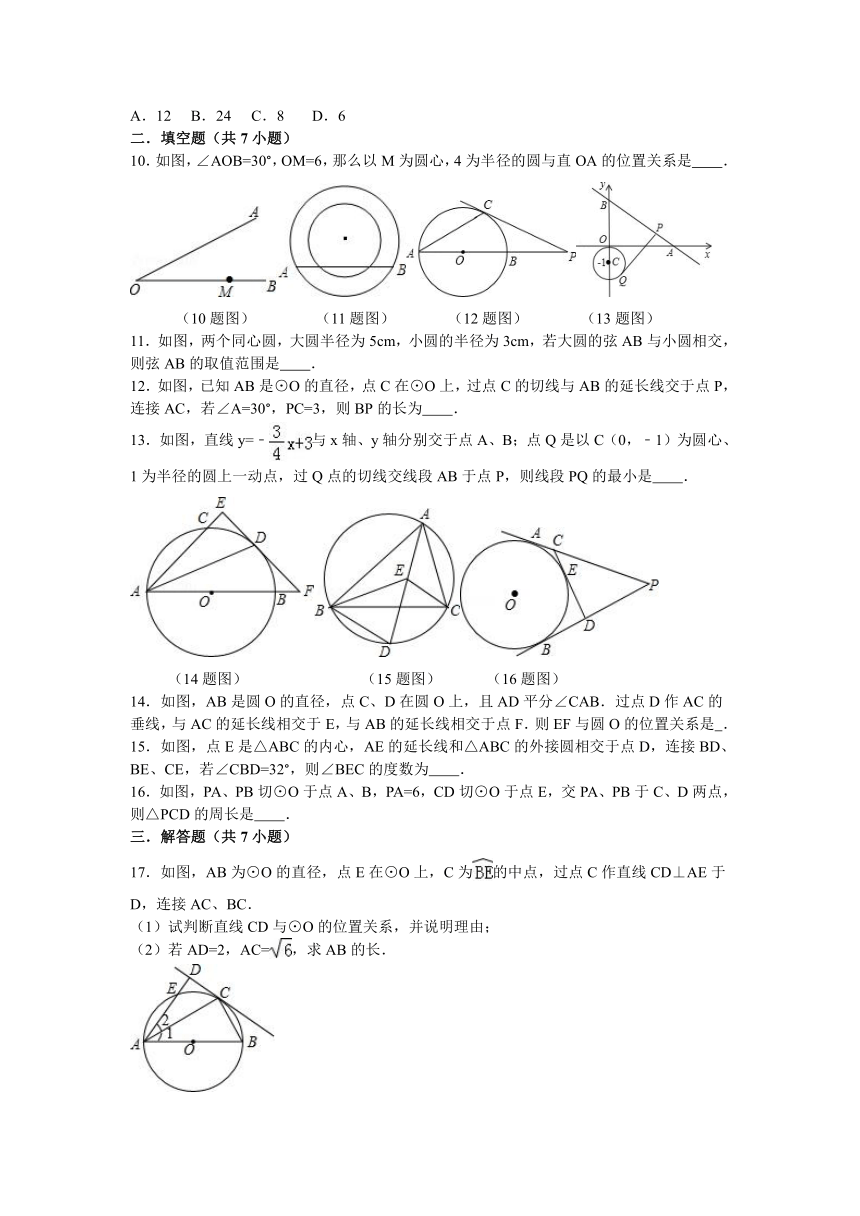
10.如图,∠AOB=30°,OM=6,那么以M为圆心,4为半径的圆与直OA的位置关系是 .
(10题图)
(11题图)
(12题图)
(13题图)
11.如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .
12.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为 .
13.如图,直线y=﹣与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
(14题图)
(15题图)
(16题图)
14.如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.则EF与圆O的位置关系是
.
15.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .
16.如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是 .
三.解答题(共7小题)
17.如图,AB为⊙O的直径,点E在⊙O上,C为的中点,过点C作直线CD⊥AE于D,连接AC、BC.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=,求AB的长.
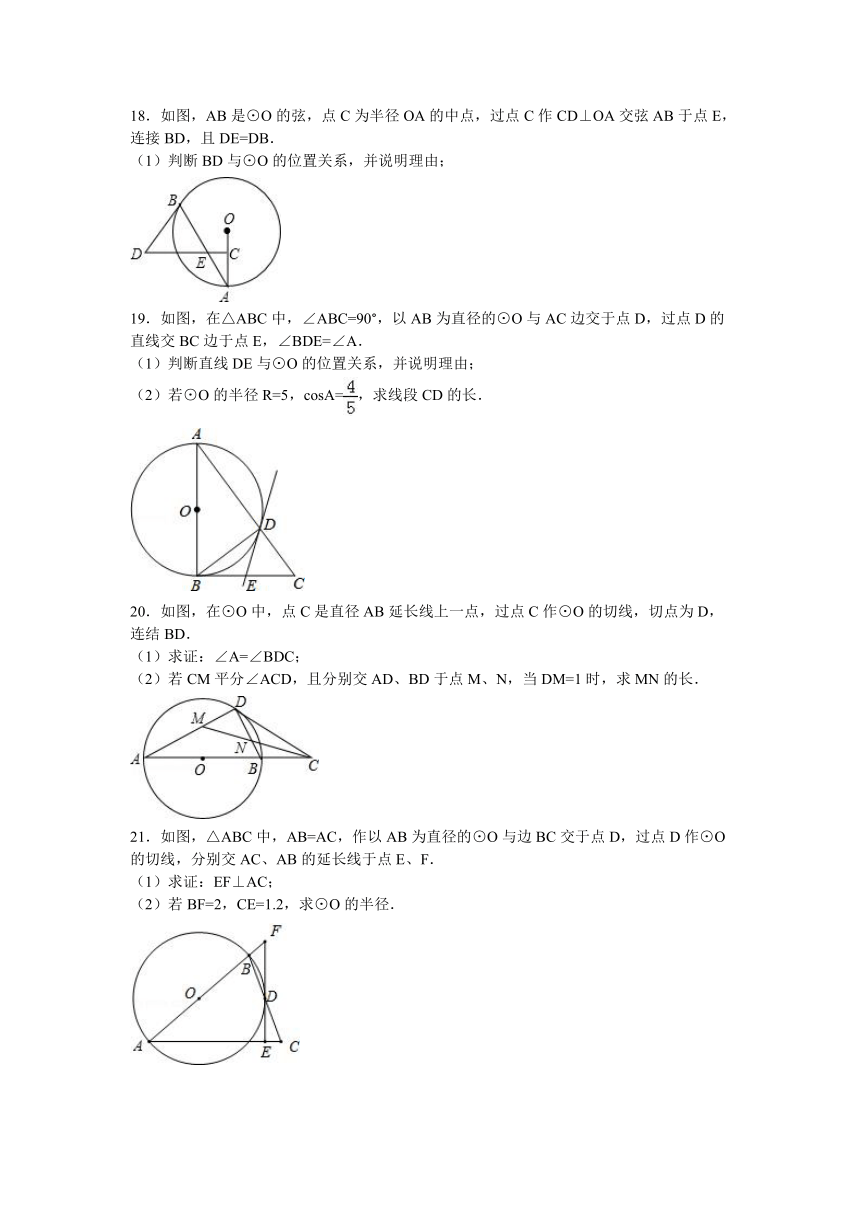
18.如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
19.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,cosA=,求线段CD的长.
20.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
21.如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
23.如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
鲁教版九年级数学下册第5单元5.6-5.7对应练习题参考答案
一.选择题(共9小题)
1.C. 2.A.3.D.4.C.
5.D.解:∵AB是⊙O的直径,∴∠ADB=90°=∠ADC,即AD⊥BC,①正确;
连接OD,∵D为BC中点,∴BD=DC,∵OA=OB,∴DO∥AC,∵DE⊥AC,∴OD⊥DE,
∵OD是半径,∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,∵∠ADB=∠ADO+∠ODB=90°,∴∠EDA=∠ODB,
∵OD=OB,∴∠B=∠ODB,∴∠EDA=∠B,∴②正确;
∵D为BC中点,AD⊥BC,∴AC=AB,∵OA=OB=AB,∴OA=AC,∴③正确.
6.B.解:∵四边形ABCD为矩形,∴△ACD≌△CAB,∴⊙P和⊙Q的半径相等.
在Rt△BC中,AB=4,BC=3,∴AC==5,
∴⊙P的半径r===1.
连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,则∠QEP=90°,如图所示.
在Rt△QEP中,QE=BC﹣2r=3﹣2=1,EP=AB﹣2r=4﹣2=2,
∴PQ===.
7.C. 8.B.9.D.
二.填空题(共7小题)
10. 相交 .11. 8<AB≤10 .12. .
13. .解:过点C作CP⊥直线AB于点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.
直线AB的解析式为y=﹣,即3x+4y﹣12=0,∴CP==.
∵PQ为⊙C的切线,∴在Rt△CQP中,CQ=1,∠CQP=90°,
∴PQ==.故答案为:.
14.证明:连接OD,如右图所示,
∵∠FOD=2∠BAD,AD平分∠CAB,∴∠EAF=2∠BAD,∴∠EAF=∠FOD,
∵AE⊥EF,∴∠AEF=90°,∴∠EAF+∠EFA=90°,∴∠DFO+∠DOF=90°,
∴∠ODF=90°,∴OD⊥EF,即EF与圆O相切.
15. 122° .16.12 .
三.解答题(共7小题)
17.解:(1)相切,连接OC,∵C为的中点,∴∠1=∠2,
∵OA=OC,∴∠1=∠ACO,∴∠2=∠ACO,∴AD∥OC,
∵CD⊥AD,∴OC⊥CD,∴直线CD与⊙O相切;
(2)∵∠DCA=∠B,易得△ADC∽△ACB,∴=,∴AB=3.
18.(1)证明:连接OB,
∵OB=OA,DE=DB,∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,∴∠A+∠AEC=∠A+∠DEB=90°,∴∠OBA+∠ABD=90°,∴OB⊥BD,
∴BD是⊙O的切线;
19.解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD∴∠ODA=∠A
又∵∠BDE=∠A∴∠ODA=∠BDE
∵AB是⊙O直径∴∠ADB=90°即∠ODA+∠ODB=90°∴∠BDE+∠ODB=90°∴∠ODE=90°
∴OD⊥DE∴DE与⊙O相切;
(2))∵R=5,∴AB=10,
在Rt△ABC中∵cosA==∴AC===,
又∵在RT△ABD中,AD=ABcosA=10×=8,∴CD=AC﹣AD=﹣8=.
20.解:(1)连接OD,
∵AB为⊙O的直径,∴∠ADB=90°,即∠A+∠ABD=90°,
又∵CD与⊙O相切于点D,∴∠CDB+∠ODB=90°,
∵OD=OB,∴∠ABD=∠ODB,∴∠A=∠BDC;
(2)∵CM平分∠ACD,∴∠DCM=∠ACM,
又∵∠A=∠BDC,
∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,
∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN==.
21.(1)证明:连接OD,AD,
∵EF是⊙O的切线,∴OD⊥EF.
又∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,∴BD=DC.∴OD∥AC.
∴AC⊥EF.
(2)解:设⊙O的半径为x.
∵OD∥AE,∴△ODF∽△AEF.
∴,即=.解得:x=3.∴⊙O的半径为3.
22.(1)证明:如图,连接OD.
∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,,∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.又∵OD是⊙O的半径,∴ED是⊙O的切线;
(2)解:如图,∵OE=10.∵AB是直径,∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO,
又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴=,
∴BC=2OE=20,即BC的长是20.
23.(1)证明:∵点E是△ABC的内心,∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,∴∠BAD=∠CBD,∴∠BED=∠ABE+∠BAD,
∴∠ABE=∠CBE,∠BAD=∠CAD=∠CBD,
∵∠EBD=∠CBE+∠CBD,∴∠BED=∠EBD,∴ED=BD;
(2)解:连接CD,
∵∠BAC=90°,∴BC是⊙O的直径,∴∠BDC=90°,
∵⊙O的直径=6,∴BC=6,
∵E为△ABC的内切圆的圆心,∴∠BAD=∠CAD,∴BD=DC,
∴BD=DC=BC=3.
一.选择题(共9小题)
1.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离
B.相切
C.相交
D.无法确定
2.在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以点C为圆心,以2.5cm为半径画圆,则⊙C与直线AB的位置关系是( )
A.相交
B.相切
C.相离
D.不能确定
3.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70°
B.35°
C.20°
D.40°
(3题图)
(4题图)
(5题图)
(6题图)
4.如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为
( )
A.40°
B.50°
C.55°
D.60°
5.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于E,连接AD,则下列结论:
①AD⊥BC;②∠EDA=∠B;③OA=AC;④DE是⊙O的切线,正确的个数是( )
A.1
个
B.2个
C.3
个
D.4个
6.如图,矩形ABCD中,AB=4,BC=3,连接AC,⊙P和⊙Q分别是△ABC和△ADC的内切圆,则PQ的长是( )
A.
B.
C.
D.2
7.圆I是三角形ABC的内切圆,D,E,F为3个切点,若∠DEF=52°,则∠A的度数为( )
A.68°
B.52°
C.76°
D.38°
(7题图)
(8题图)
(9题图)
8.如图,PA、PB、CD与⊙O相切于点为A、B、E,若PA=7,则△PCD的周长为( )
A.7
B.14
C.10.5
D.10
9.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12
B.24
C.8
D.6
二.填空题(共7小题)
10.如图,∠AOB=30°,OM=6,那么以M为圆心,4为半径的圆与直OA的位置关系是 .
(10题图)
(11题图)
(12题图)
(13题图)
11.如图,两个同心圆,大圆半径为5cm,小圆的半径为3cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是 .
12.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为 .
13.如图,直线y=﹣与x轴、y轴分别交于点A、B;点Q是以C(0,﹣1)为圆心、1为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小是 .
(14题图)
(15题图)
(16题图)
14.如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.则EF与圆O的位置关系是
.
15.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .
16.如图,PA、PB切⊙O于点A、B,PA=6,CD切⊙O于点E,交PA、PB于C、D两点,则△PCD的周长是 .
三.解答题(共7小题)
17.如图,AB为⊙O的直径,点E在⊙O上,C为的中点,过点C作直线CD⊥AE于D,连接AC、BC.
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=,求AB的长.
18.如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
19.如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,cosA=,求线段CD的长.
20.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.
(1)求证:∠A=∠BDC;
(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.
21.如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
23.如图,点E是△ABC的内心,线段AE的延长线交△ABC的外接圆于点D.
(1)求证:ED=BD;
(2)若∠BAC=90°,△ABC的外接圆的直径是6,求BD的长.
鲁教版九年级数学下册第5单元5.6-5.7对应练习题参考答案
一.选择题(共9小题)
1.C. 2.A.3.D.4.C.
5.D.解:∵AB是⊙O的直径,∴∠ADB=90°=∠ADC,即AD⊥BC,①正确;
连接OD,∵D为BC中点,∴BD=DC,∵OA=OB,∴DO∥AC,∵DE⊥AC,∴OD⊥DE,
∵OD是半径,∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,∵∠ADB=∠ADO+∠ODB=90°,∴∠EDA=∠ODB,
∵OD=OB,∴∠B=∠ODB,∴∠EDA=∠B,∴②正确;
∵D为BC中点,AD⊥BC,∴AC=AB,∵OA=OB=AB,∴OA=AC,∴③正确.
6.B.解:∵四边形ABCD为矩形,∴△ACD≌△CAB,∴⊙P和⊙Q的半径相等.
在Rt△BC中,AB=4,BC=3,∴AC==5,
∴⊙P的半径r===1.
连接点P、Q,过点Q作QE∥BC,过点P作PE∥AB交QE于点E,则∠QEP=90°,如图所示.
在Rt△QEP中,QE=BC﹣2r=3﹣2=1,EP=AB﹣2r=4﹣2=2,
∴PQ===.
7.C. 8.B.9.D.
二.填空题(共7小题)
10. 相交 .11. 8<AB≤10 .12. .
13. .解:过点C作CP⊥直线AB于点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.
直线AB的解析式为y=﹣,即3x+4y﹣12=0,∴CP==.
∵PQ为⊙C的切线,∴在Rt△CQP中,CQ=1,∠CQP=90°,
∴PQ==.故答案为:.
14.证明:连接OD,如右图所示,
∵∠FOD=2∠BAD,AD平分∠CAB,∴∠EAF=2∠BAD,∴∠EAF=∠FOD,
∵AE⊥EF,∴∠AEF=90°,∴∠EAF+∠EFA=90°,∴∠DFO+∠DOF=90°,
∴∠ODF=90°,∴OD⊥EF,即EF与圆O相切.
15. 122° .16.12 .
三.解答题(共7小题)
17.解:(1)相切,连接OC,∵C为的中点,∴∠1=∠2,
∵OA=OC,∴∠1=∠ACO,∴∠2=∠ACO,∴AD∥OC,
∵CD⊥AD,∴OC⊥CD,∴直线CD与⊙O相切;
(2)∵∠DCA=∠B,易得△ADC∽△ACB,∴=,∴AB=3.
18.(1)证明:连接OB,
∵OB=OA,DE=DB,∴∠A=∠OBA,∠DEB=∠ABD,
又∵CD⊥OA,∴∠A+∠AEC=∠A+∠DEB=90°,∴∠OBA+∠ABD=90°,∴OB⊥BD,
∴BD是⊙O的切线;
19.解:(1)直线DE与⊙O相切.
理由如下:连接OD.
∵OA=OD∴∠ODA=∠A
又∵∠BDE=∠A∴∠ODA=∠BDE
∵AB是⊙O直径∴∠ADB=90°即∠ODA+∠ODB=90°∴∠BDE+∠ODB=90°∴∠ODE=90°
∴OD⊥DE∴DE与⊙O相切;
(2))∵R=5,∴AB=10,
在Rt△ABC中∵cosA==∴AC===,
又∵在RT△ABD中,AD=ABcosA=10×=8,∴CD=AC﹣AD=﹣8=.
20.解:(1)连接OD,
∵AB为⊙O的直径,∴∠ADB=90°,即∠A+∠ABD=90°,
又∵CD与⊙O相切于点D,∴∠CDB+∠ODB=90°,
∵OD=OB,∴∠ABD=∠ODB,∴∠A=∠BDC;
(2)∵CM平分∠ACD,∴∠DCM=∠ACM,
又∵∠A=∠BDC,
∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,
∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN==.
21.(1)证明:连接OD,AD,
∵EF是⊙O的切线,∴OD⊥EF.
又∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC.
又∵AB=AC,∴BD=DC.∴OD∥AC.
∴AC⊥EF.
(2)解:设⊙O的半径为x.
∵OD∥AE,∴△ODF∽△AEF.
∴,即=.解得:x=3.∴⊙O的半径为3.
22.(1)证明:如图,连接OD.
∵AC⊥AB,∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,,∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.又∵OD是⊙O的半径,∴ED是⊙O的切线;
(2)解:如图,∵OE=10.∵AB是直径,∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,∴∠AEO=∠DEO,
又∵AE=DE,∴OE⊥AD,∴OE∥BC,∴=,
∴BC=2OE=20,即BC的长是20.
23.(1)证明:∵点E是△ABC的内心,∴∠BAD=∠CAD,∠ABE=∠CBE,
∵∠CBD=∠CAD,∴∠BAD=∠CBD,∴∠BED=∠ABE+∠BAD,
∴∠ABE=∠CBE,∠BAD=∠CAD=∠CBD,
∵∠EBD=∠CBE+∠CBD,∴∠BED=∠EBD,∴ED=BD;
(2)解:连接CD,
∵∠BAC=90°,∴BC是⊙O的直径,∴∠BDC=90°,
∵⊙O的直径=6,∴BC=6,
∵E为△ABC的内切圆的圆心,∴∠BAD=∠CAD,∴BD=DC,
∴BD=DC=BC=3.
