人教版九年级上册同步教学习题课件:24.1.2 垂直于弦的直径
文档属性
| 名称 | 人教版九年级上册同步教学习题课件:24.1.2 垂直于弦的直径 |

|
|
| 格式 | zip | ||
| 文件大小 | 419.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-11 21:15:02 | ||
图片预览




文档简介
课件14张PPT。九年级数学·上 新课标 [人]第二十四章 圆24.1.2 垂直于弦的直径
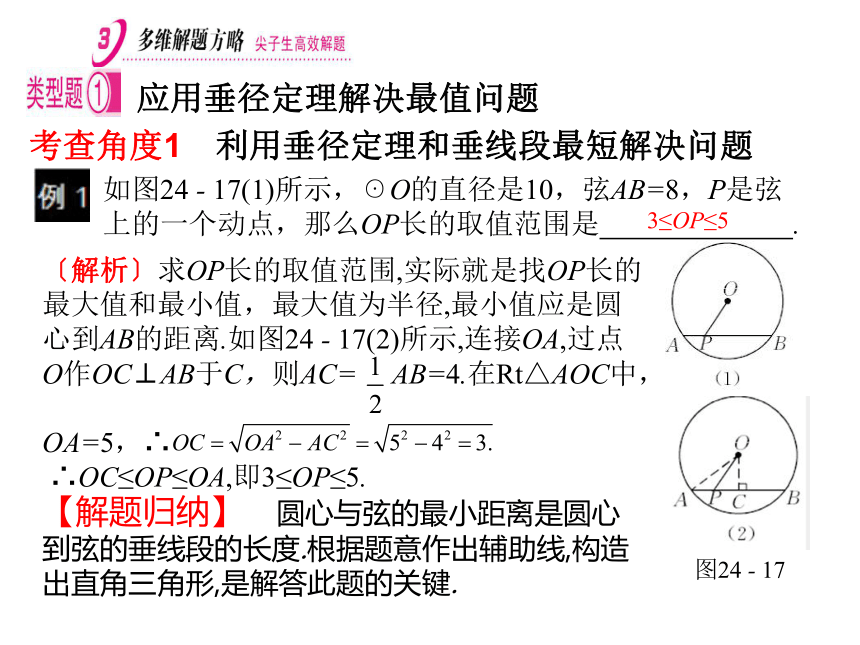
24.1 圆的有关性质〔解析〕求OP长的取值范围,实际就是找OP长的最大值和最小值,最大值为半径,最小值应是圆心到AB的距离.如图24 - 17(2)所示,连接OA,过点O作OC⊥AB于C,则AC= AB=4.在Rt△AOC中,
OA=5,∴
∴OC≤OP≤OA,即3≤OP≤5. 应用垂径定理解决最值问题考查角度1 利用垂径定理和垂线段最短解决问题如图24 - 17(1)所示,☉O的直径是10,弦AB=8,P是弦上的一个动点,那么OP长的取值范围是 .图24 - 17【解题归纳】 圆心与弦的最小距离是圆心到弦的垂线段的长度.根据题意作出辅助线,构造出直角三角形,是解答此题的关键. 3≤OP≤51.(2015·岳池模拟)如图所示,☉O的半径为5,弦AB的长为6,M是AB上的动点,则线段OM长的最小值为 ( )
A.2 B.3 C.4 D.5C考查角度2 利用垂径定理解决线段和最短问题例2 (张家界中考)如图24 - 18所示,
AB,CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .?〔解析〕 如图24 - 19所示,连接OA,OB,OC,BC,作CH垂直AB于H.根据垂径定理,
得BE= AB=4,CF= CD=3,∴OE=
OF= ∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7.在直角三角形BCH中,根据勾股定理得BC= , 则PA+PC的最小值为 . 【解题归纳】 当直径垂直于圆的一条弦时,直径所在的直线是这条弦的垂直平分线,同时,圆的任意一条直径所在的直线均为圆的对称轴.本题利用圆的对称性和垂径定理把PA+PC的最小值转化为BC的长.2.(东营中考)如图,在☉O中,AB是☉O的直径,AB=8 cm, M是AB上一动点,CM+DM的最小值为 cm.?[提示:如图56所示,过点C作CE⊥AB交☉O于点E,连接ED,EM,由圆的对称性知EM=CM,EM+DM>DE,当点M运动到AB与DE的交点时,CM+DM的值最小,最小值为圆的直径8 cm.] 8利用垂径定理解决实际问题例3把球放在长方体纸盒内,球的一部分露出盒外,其截面如图24 - 20所示,已知圆心为O,EF=CD=16厘米,则☉O的半径为多少厘米?解:过点O作OM⊥AD于点M,连接OF,如图24 - 20所示.设OF=x,则OM=16-x,MF=8,在直角三角形OMF中,OM2+MF2=OF2,即(16-x)2+82=x2,解得x=10.答:☉O的半径为10厘米.
3.温州是著名水乡,河流遍布整个城市.某河流上建有一座美丽的石拱桥(平面图如图所示).已知桥
拱半径OC为5 m,水面宽AB为 m,则石拱桥
的桥顶到水面的距离CD为 ( ) [提示:连接OA,∵CD⊥AB,∴AD=BD= AB= ×4
=2 .在Rt△OAD中,OA=5 m,AD=2 m,∴OD=
=1(m),∴CD=OC+OD=5+1=6(m).]A. m B.7 m
C. m D.6 mD在Rt△OPD中,∵OP= ,OD=3,
∴PD= =2,
又∵点P在第一象限,∴点P的坐标为(3,2). 垂径定理与平面直角坐标系的综合应用例4(广州中考)如图24 - 21所示,在平面直角坐标系中,点O为坐标原点,点P在第一象限,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为 ,则点P的坐标为 .?图24 - 21〔解析〕 如图24 - 21所示,过点P作PD⊥x轴于点D,连接OP,∵A(6,0),PD⊥OA,∴OD= OA=3.(3,2)4.如图所示,半径为6的☉E在平面直角坐标系中,与x轴交于A,B两点,与y轴交于C,D两点,且点E在第四象限,已知C(0,3),D(0,-7),求圆心E的坐标.解:如图57所示,过点E作EN⊥x轴于点N,作EM⊥y轴于点M,连接DE.∵C点的坐标为(0,3),D点的坐标为(0,-7),∴CD=3-(-7)=10,又∵EM⊥CD,∴MD= CD=5.在Rt△DEM中,由勾股定理得EM= .∵四边形OMEN为矩形,∴EN=OM=OD-MD=7-5=2.又∵点E在第四象限,∴圆心E的坐标为( ,-2). 利用“分类讨论”解圆中的计算问题 已知AB,CD为☉O的两条平行弦,☉O的半径为5 cm,AB=8 cm,CD=6 cm,求弦AB,CD间的距离.〔解析〕 由于题目中只说弦AB,CD平行,没有说明这两条弦与圆心的位置关系,因此需要对两弦与圆心的位置关系进行讨论.例5例5所以OE= =3(cm).所以OF= =4 cm.解:分两种情况:①当AB,CD在圆心O的同侧时,如图(1)所示,过O作OF⊥CD于点F,OF交AB于点E.连接OA,OC.因为AB∥CD,所以OE⊥AB.因为OF⊥CD,CD=6 cm,所以CF= CD=3 cm.在Rt△OCF中,因为OC=5 cm,CF=3 cm,因为OE⊥AB,AB=8 cm,所以AE= AB=4 cm.在Rt△OAE中,因为OA=5 cm,AE=4 cm,所以EF=OF-OE=4-3=1(cm).②当AB,CD在圆心O的两侧时,如图(2)所示,过O作OF⊥CD于点F,OF的反向延长线交AB于点E,连接OA,OC.因为AB∥CD,所以OE⊥AB.所以EF=OE+OF=3+4=7(cm).综上所述,弦AB,CD间的距离为1 cm或7 cm.同① ,可得OE=3cm,OF=4cm.在Rt△AOE中, OE=
∴OF=OE+EF=5+7=12.在Rt△OCF中, CF=
∴CD=2CF=2×5=10. 5.(牡丹江中考)在半径为13的☉O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为 ( )A.10B.4C.10或4 D.10或2 [提示:当AB与CD在圆心O的同侧时,如图(1)所示,过点O作OF⊥CD于点F,交AB于点E,连接OA,OC.∵AB∥CD,OF⊥CD,∴OE⊥AB,∴AE= AB= ×24=12.当AB与CD在圆心O的两侧时,如图(2)所示.
过点O作OF⊥CD于点F,反向延长OF交AB于
点E,连接OA,OC,CF= ,OE= =5,∴OF=EF-OE=7-5=2.在Rt△AOE中,在Rt△OCF中,∴CD=2CF=2× =2 .故CD的长为10或2 .]∵AB∥CD,OF⊥CD,∴OE⊥AB,
∴AE= AB= ×24=12.
24.1 圆的有关性质〔解析〕求OP长的取值范围,实际就是找OP长的最大值和最小值,最大值为半径,最小值应是圆心到AB的距离.如图24 - 17(2)所示,连接OA,过点O作OC⊥AB于C,则AC= AB=4.在Rt△AOC中,
OA=5,∴
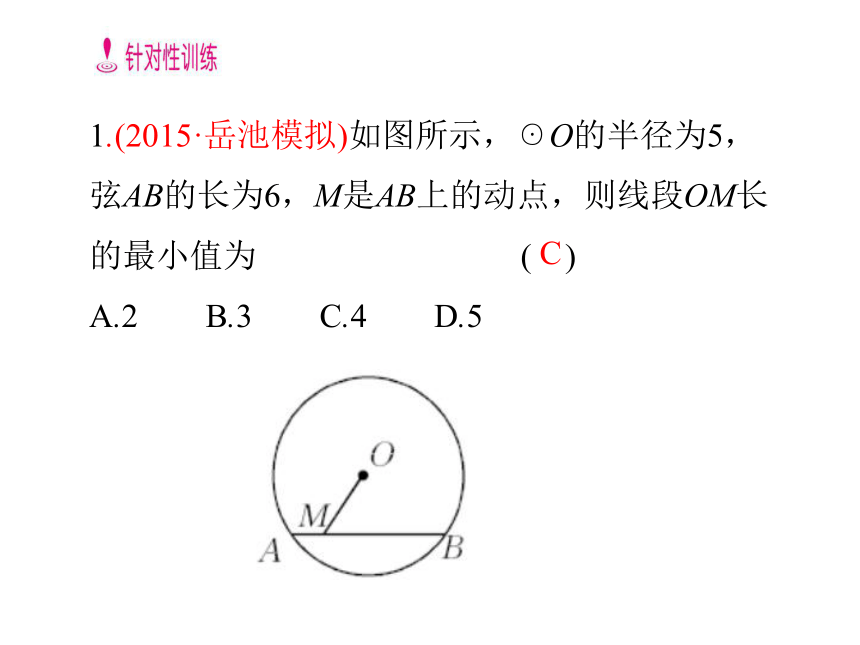
∴OC≤OP≤OA,即3≤OP≤5. 应用垂径定理解决最值问题考查角度1 利用垂径定理和垂线段最短解决问题如图24 - 17(1)所示,☉O的直径是10,弦AB=8,P是弦上的一个动点,那么OP长的取值范围是 .图24 - 17【解题归纳】 圆心与弦的最小距离是圆心到弦的垂线段的长度.根据题意作出辅助线,构造出直角三角形,是解答此题的关键. 3≤OP≤51.(2015·岳池模拟)如图所示,☉O的半径为5,弦AB的长为6,M是AB上的动点,则线段OM长的最小值为 ( )
A.2 B.3 C.4 D.5C考查角度2 利用垂径定理解决线段和最短问题例2 (张家界中考)如图24 - 18所示,
AB,CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .?〔解析〕 如图24 - 19所示,连接OA,OB,OC,BC,作CH垂直AB于H.根据垂径定理,
得BE= AB=4,CF= CD=3,∴OE=
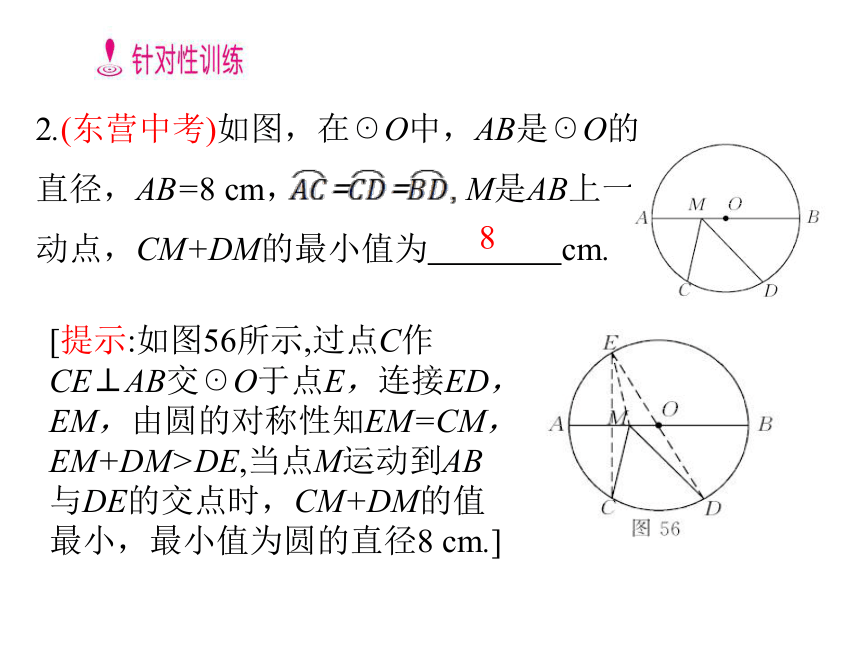
OF= ∴CH=OE+OF=3+4=7,BH=BE+EH=BE+CF=4+3=7.在直角三角形BCH中,根据勾股定理得BC= , 则PA+PC的最小值为 . 【解题归纳】 当直径垂直于圆的一条弦时,直径所在的直线是这条弦的垂直平分线,同时,圆的任意一条直径所在的直线均为圆的对称轴.本题利用圆的对称性和垂径定理把PA+PC的最小值转化为BC的长.2.(东营中考)如图,在☉O中,AB是☉O的直径,AB=8 cm, M是AB上一动点,CM+DM的最小值为 cm.?[提示:如图56所示,过点C作CE⊥AB交☉O于点E,连接ED,EM,由圆的对称性知EM=CM,EM+DM>DE,当点M运动到AB与DE的交点时,CM+DM的值最小,最小值为圆的直径8 cm.] 8利用垂径定理解决实际问题例3把球放在长方体纸盒内,球的一部分露出盒外,其截面如图24 - 20所示,已知圆心为O,EF=CD=16厘米,则☉O的半径为多少厘米?解:过点O作OM⊥AD于点M,连接OF,如图24 - 20所示.设OF=x,则OM=16-x,MF=8,在直角三角形OMF中,OM2+MF2=OF2,即(16-x)2+82=x2,解得x=10.答:☉O的半径为10厘米.
3.温州是著名水乡,河流遍布整个城市.某河流上建有一座美丽的石拱桥(平面图如图所示).已知桥
拱半径OC为5 m,水面宽AB为 m,则石拱桥
的桥顶到水面的距离CD为 ( ) [提示:连接OA,∵CD⊥AB,∴AD=BD= AB= ×4
=2 .在Rt△OAD中,OA=5 m,AD=2 m,∴OD=
=1(m),∴CD=OC+OD=5+1=6(m).]A. m B.7 m
C. m D.6 mD在Rt△OPD中,∵OP= ,OD=3,
∴PD= =2,
又∵点P在第一象限,∴点P的坐标为(3,2). 垂径定理与平面直角坐标系的综合应用例4(广州中考)如图24 - 21所示,在平面直角坐标系中,点O为坐标原点,点P在第一象限,☉P与x轴交于O,A两点,点A的坐标为(6,0),☉P的半径为 ,则点P的坐标为 .?图24 - 21〔解析〕 如图24 - 21所示,过点P作PD⊥x轴于点D,连接OP,∵A(6,0),PD⊥OA,∴OD= OA=3.(3,2)4.如图所示,半径为6的☉E在平面直角坐标系中,与x轴交于A,B两点,与y轴交于C,D两点,且点E在第四象限,已知C(0,3),D(0,-7),求圆心E的坐标.解:如图57所示,过点E作EN⊥x轴于点N,作EM⊥y轴于点M,连接DE.∵C点的坐标为(0,3),D点的坐标为(0,-7),∴CD=3-(-7)=10,又∵EM⊥CD,∴MD= CD=5.在Rt△DEM中,由勾股定理得EM= .∵四边形OMEN为矩形,∴EN=OM=OD-MD=7-5=2.又∵点E在第四象限,∴圆心E的坐标为( ,-2). 利用“分类讨论”解圆中的计算问题 已知AB,CD为☉O的两条平行弦,☉O的半径为5 cm,AB=8 cm,CD=6 cm,求弦AB,CD间的距离.〔解析〕 由于题目中只说弦AB,CD平行,没有说明这两条弦与圆心的位置关系,因此需要对两弦与圆心的位置关系进行讨论.例5例5所以OE= =3(cm).所以OF= =4 cm.解:分两种情况:①当AB,CD在圆心O的同侧时,如图(1)所示,过O作OF⊥CD于点F,OF交AB于点E.连接OA,OC.因为AB∥CD,所以OE⊥AB.因为OF⊥CD,CD=6 cm,所以CF= CD=3 cm.在Rt△OCF中,因为OC=5 cm,CF=3 cm,因为OE⊥AB,AB=8 cm,所以AE= AB=4 cm.在Rt△OAE中,因为OA=5 cm,AE=4 cm,所以EF=OF-OE=4-3=1(cm).②当AB,CD在圆心O的两侧时,如图(2)所示,过O作OF⊥CD于点F,OF的反向延长线交AB于点E,连接OA,OC.因为AB∥CD,所以OE⊥AB.所以EF=OE+OF=3+4=7(cm).综上所述,弦AB,CD间的距离为1 cm或7 cm.同① ,可得OE=3cm,OF=4cm.在Rt△AOE中, OE=
∴OF=OE+EF=5+7=12.在Rt△OCF中, CF=
∴CD=2CF=2×5=10. 5.(牡丹江中考)在半径为13的☉O中,弦AB∥CD,弦AB和CD的距离为7,若AB=24,则CD的长为 ( )A.10B.4C.10或4 D.10或2 [提示:当AB与CD在圆心O的同侧时,如图(1)所示,过点O作OF⊥CD于点F,交AB于点E,连接OA,OC.∵AB∥CD,OF⊥CD,∴OE⊥AB,∴AE= AB= ×24=12.当AB与CD在圆心O的两侧时,如图(2)所示.
过点O作OF⊥CD于点F,反向延长OF交AB于
点E,连接OA,OC,CF= ,OE= =5,∴OF=EF-OE=7-5=2.在Rt△AOE中,在Rt△OCF中,∴CD=2CF=2× =2 .故CD的长为10或2 .]∵AB∥CD,OF⊥CD,∴OE⊥AB,
∴AE= AB= ×24=12.
同课章节目录
