人教版九年级上册同步教学课件:24.4 弧长和扇形面积
文档属性
| 名称 | 人教版九年级上册同步教学课件:24.4 弧长和扇形面积 |

|
|
| 格式 | zip | ||
| 文件大小 | 389.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-12 11:10:30 | ||
图片预览






文档简介
课件15张PPT。第二十四章 圆24.4 弧长和扇形面积九年级数学·上 新课标 [人] 〔解析〕 点P运动的路径长为圆心角为60°,半径分别为12,10,8,6,4,2的扇形弧长的和,即路径长为:应用弧长公式解决运动轨迹问题 (日照中考)如图24 - 130所示,正六边形ABCDEF是边长为2 cm的螺母,点P是FA延长线上的点,在A,P之间
拉一条长为12 cm的无伸缩性细线,一端固定在点A,
握住另一端点P拉直细线,把它全部紧紧缠绕在螺母
上(缠绕时螺母不动),则点P运动的路径长为 ( )
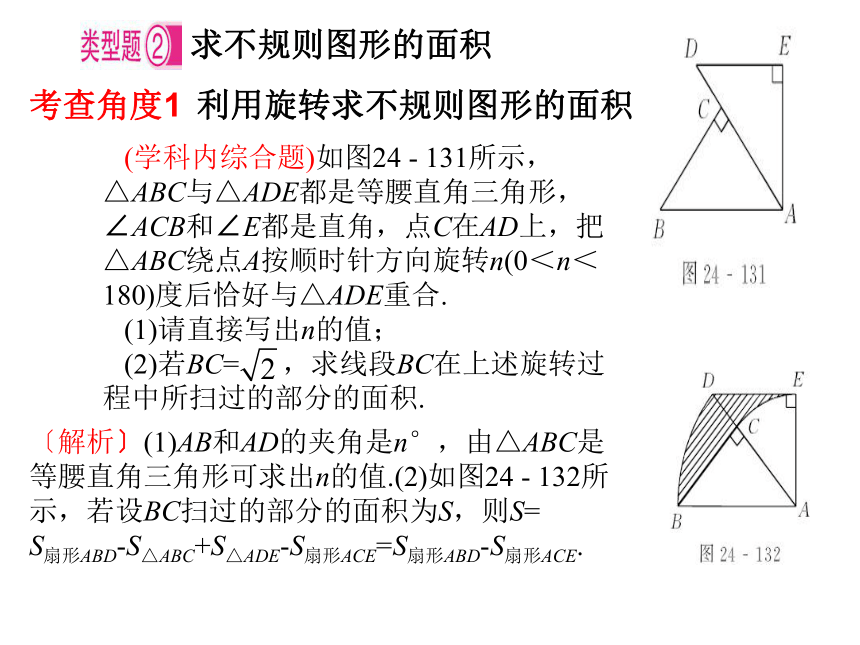
A.13π cm B.14π cm C.15π cm D.16π cm【解题归纳】 对整个运动过程进行分析,弄清点P所走过的路线,关键是要确定每一次旋转的旋转中心及旋转半径,正确画出路径,找出半径的变化规律,然后运用弧长公式求出几段路径的弧长之和.B1.(兰州中考)如图所示,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕直角顶点C逆时针旋转60°得△A'B'C,则点B转过的路径长为 ( ) [提示:在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,可得AC=1,由勾股定理可得BC= ,由旋转知点B转过的路径是一段圆弧,其所对的圆心角为60°,利用弧长公式得 .]B求不规则图形的面积考查角度1利用旋转求不规则图形的面积例2(学科内综合题)如图24 - 131所示,△ABC与△ADE都是等腰直角三角形,∠ACB和∠E都是直角,点C在AD上,把△ABC绕点A按顺时针方向旋转n(0<n<180)度后恰好与△ADE重合.
(1)请直接写出n的值;
(2)若BC= ,求线段BC在上述旋转过程中所扫过的部分的面积.〔解析〕(1)AB和AD的夹角是n°,由△ABC是等腰直角三角形可求出n的值.(2)如图24 - 132所示,若设BC扫过的部分的面积为S,则S=
S扇形ABD-S△ABC+S△ADE-S扇形ACE=S扇形ABD-S扇形ACE.解:(1)n=45.(2)设在旋转过程中,线段BC所扫过的部分的面积(即图24 - 132中阴影部分的面积)为S,
则S=S扇形ABD-S△ABC+S△ADE-S扇形ACE.又∵S△ABC=S△ADE,∴S=S扇形ABD-S扇形ACE.
在Rt△ABC中,BC= ,∠BAC=45°,∠BCA=90°,∴由勾股定理,可得AB=又∵AC=BC=2.(2015·乐山中考)如图所示,已知A( ,2),B( ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A'(-2, )的位置,则图中阴影部分的面积为 .?[提示:由题意知旋转了90°,
所以n=90,通过割补易得S阴=S扇形OAA'-S扇形OBB'=考查角度2 利用整体思想求不规则图形的面积例3如图24 - 133所示,☉A,☉B,☉C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为 ( ) A.π B. π
C.2π D. π 设∠A=α°,∠B=β°,∠C=γ°,∵∠A+∠B+∠C=180°,∴阴影部分的面积=〔解析〕B【解题归纳】 解决本题的关键不是求出三角形三个内角的度数,而是应用整体思想求出三个内角的和,然后根据扇形面积公式计算.3.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在以五边形各顶点为圆心,2 m长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是 ( )
A.6π m2 B.5π m2
C.4π m2 D.3π m2A∴CD= .∴S△DCO= CO·DC= ,(2015·鄂尔多斯中考)如图24 - 134所示,某实践小组要在广场一角的扇形区域内种植红、黄两种花,∠AOB=90°,半径OA=4米,C是OA的中点,点D在 上,CD∥OB,则图中种植黄花(即阴影部分)的面积是 (结果保留π). ?考查角度3 利用割补法求阴影部分的面积例4〔解析〕 如图24 - 135所示,连接DO,DA,∵∠AOB=90°,CD∥OB,∴∠DCO=90°.∵C是OA的中点,∴DC是AO的垂直平分线.∴DA=DO.∵OD=OA,∴AO=DO=AD.∴△AOD是等边三角形,∴∠DOA=60°.又在Rt△DCO中,OD=4,∴OC=2,∵S扇形OAD= ,∴S阴影= S扇形OAD-S△DCO=【解题归纳】 求解一些几何图形的面积,特别是不规则几何图形的面积时,割补法是常用的方法之一,即通过分割或补形,把不规则图形面积转化为规则图形面积的和或差,使复杂问题简单化.
4.(泰安中考)如图所示,半径为2 cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为 ( ) C.1 cm2[提示:如图95所示,设以OB为直径的半圆的圆心为O1,以OA为直径的半圆的圆心为O2,连接O1C,O2C,易知OO1=O1C=O2C=OO2=1 cm.又∠AOB=90°,则四边形O1CO2O为正方形,其面积为1 cm2.A〔解析〕 ∵CD⊥AB,CD= ,∴∠AEC =∠OED=90°,CE=DE= .∵∠C=30°,∴∠AOD=60°,∴∠ODE=30°,∴OE= OD.考查角度4 等积变形法求阴影部分的面积例5 如图24 - 136所示,AB是☉O的直径,弦CD⊥AB于E,∠C=30°,CD= ,则S阴影等于 ( )
A.π B.2π C. D. 在Rt△ODE中,由勾股定理易得OD=2,
∴ S扇形OAD= .在△ACE和△ODE中,∠AEC=∠OED,CE=DE,∠C=∠ODE,∴△ACE≌△ODE, ∴S阴影=S扇形OAD= .D[提示:如图96所示,连接OC,OD,∵∠CAD=30°,∴∠COD=60°.
∵AB∥CD,∴S△ACD=S△COD.
∴S阴影=S扇形OCD= ] 5.如图所示,半圆的直径AB=10,弦CD∥
AB,且∠CAD=30°,则图中阴影部分的面积为 .?则2π·2= ,∴n=120,即∠APA'=120°,则∠APB=60°.连接AB,AD,则△APB为等边三角形.∵D是PB的中点,∴AD⊥PB.∴AD= ,
∴蚂蚁爬行的最短路程为 .利用圆锥的侧面展开图求最短距离如图24 - 137所示,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为 ( )A. B.2 C.3 D.3〔解析〕 如图24 - 138所示,将圆锥的侧面展开,由 的长求∠APA'的度数,设∠APA'的度数为n°,例6C解:如图97所示,将圆锥的侧面展开得到扇形SAA',则这条公路的最短路程是AC'的长.在Rt△OBS中,∵OB=4千米,OS= 千米,∴SB= =16千米,∴SA=16千
米,SC' =8千米, =8π千米.设圆心角∠ASA'的度数为n°,则8π= ,解得n=90,∴∠ASA'=90°.在Rt△ASC'中,AC' = 千米.答:这条公路的最短路程为 千米.6.如图所示,有一座大山,大致呈圆锥形,底面半径为4千米,山高为 千米,在山坡SA中点C处有一联络站,要从山脚A修一盘山路,绕山坡一周将物资运往C处,这条公路的最短路程是多少?图97
拉一条长为12 cm的无伸缩性细线,一端固定在点A,
握住另一端点P拉直细线,把它全部紧紧缠绕在螺母
上(缠绕时螺母不动),则点P运动的路径长为 ( )
A.13π cm B.14π cm C.15π cm D.16π cm【解题归纳】 对整个运动过程进行分析,弄清点P所走过的路线,关键是要确定每一次旋转的旋转中心及旋转半径,正确画出路径,找出半径的变化规律,然后运用弧长公式求出几段路径的弧长之和.B1.(兰州中考)如图所示,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,将△ABC绕直角顶点C逆时针旋转60°得△A'B'C,则点B转过的路径长为 ( ) [提示:在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,可得AC=1,由勾股定理可得BC= ,由旋转知点B转过的路径是一段圆弧,其所对的圆心角为60°,利用弧长公式得 .]B求不规则图形的面积考查角度1利用旋转求不规则图形的面积例2(学科内综合题)如图24 - 131所示,△ABC与△ADE都是等腰直角三角形,∠ACB和∠E都是直角,点C在AD上,把△ABC绕点A按顺时针方向旋转n(0<n<180)度后恰好与△ADE重合.
(1)请直接写出n的值;
(2)若BC= ,求线段BC在上述旋转过程中所扫过的部分的面积.〔解析〕(1)AB和AD的夹角是n°,由△ABC是等腰直角三角形可求出n的值.(2)如图24 - 132所示,若设BC扫过的部分的面积为S,则S=
S扇形ABD-S△ABC+S△ADE-S扇形ACE=S扇形ABD-S扇形ACE.解:(1)n=45.(2)设在旋转过程中,线段BC所扫过的部分的面积(即图24 - 132中阴影部分的面积)为S,
则S=S扇形ABD-S△ABC+S△ADE-S扇形ACE.又∵S△ABC=S△ADE,∴S=S扇形ABD-S扇形ACE.
在Rt△ABC中,BC= ,∠BAC=45°,∠BCA=90°,∴由勾股定理,可得AB=又∵AC=BC=2.(2015·乐山中考)如图所示,已知A( ,2),B( ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A'(-2, )的位置,则图中阴影部分的面积为 .?[提示:由题意知旋转了90°,
所以n=90,通过割补易得S阴=S扇形OAA'-S扇形OBB'=考查角度2 利用整体思想求不规则图形的面积例3如图24 - 133所示,☉A,☉B,☉C两两不相交,且半径均为1,则图中三个阴影扇形的面积之和为 ( ) A.π B. π
C.2π D. π 设∠A=α°,∠B=β°,∠C=γ°,∵∠A+∠B+∠C=180°,∴阴影部分的面积=〔解析〕B【解题归纳】 解决本题的关键不是求出三角形三个内角的度数,而是应用整体思想求出三个内角的和,然后根据扇形面积公式计算.3.某花园内有一块五边形的空地如图所示,为了美化环境,现计划在以五边形各顶点为圆心,2 m长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是 ( )
A.6π m2 B.5π m2
C.4π m2 D.3π m2A∴CD= .∴S△DCO= CO·DC= ,(2015·鄂尔多斯中考)如图24 - 134所示,某实践小组要在广场一角的扇形区域内种植红、黄两种花,∠AOB=90°,半径OA=4米,C是OA的中点,点D在 上,CD∥OB,则图中种植黄花(即阴影部分)的面积是 (结果保留π). ?考查角度3 利用割补法求阴影部分的面积例4〔解析〕 如图24 - 135所示,连接DO,DA,∵∠AOB=90°,CD∥OB,∴∠DCO=90°.∵C是OA的中点,∴DC是AO的垂直平分线.∴DA=DO.∵OD=OA,∴AO=DO=AD.∴△AOD是等边三角形,∴∠DOA=60°.又在Rt△DCO中,OD=4,∴OC=2,∵S扇形OAD= ,∴S阴影= S扇形OAD-S△DCO=【解题归纳】 求解一些几何图形的面积,特别是不规则几何图形的面积时,割补法是常用的方法之一,即通过分割或补形,把不规则图形面积转化为规则图形面积的和或差,使复杂问题简单化.
4.(泰安中考)如图所示,半径为2 cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为 ( ) C.1 cm2[提示:如图95所示,设以OB为直径的半圆的圆心为O1,以OA为直径的半圆的圆心为O2,连接O1C,O2C,易知OO1=O1C=O2C=OO2=1 cm.又∠AOB=90°,则四边形O1CO2O为正方形,其面积为1 cm2.A〔解析〕 ∵CD⊥AB,CD= ,∴∠AEC =∠OED=90°,CE=DE= .∵∠C=30°,∴∠AOD=60°,∴∠ODE=30°,∴OE= OD.考查角度4 等积变形法求阴影部分的面积例5 如图24 - 136所示,AB是☉O的直径,弦CD⊥AB于E,∠C=30°,CD= ,则S阴影等于 ( )
A.π B.2π C. D. 在Rt△ODE中,由勾股定理易得OD=2,
∴ S扇形OAD= .在△ACE和△ODE中,∠AEC=∠OED,CE=DE,∠C=∠ODE,∴△ACE≌△ODE, ∴S阴影=S扇形OAD= .D[提示:如图96所示,连接OC,OD,∵∠CAD=30°,∴∠COD=60°.
∵AB∥CD,∴S△ACD=S△COD.
∴S阴影=S扇形OCD= ] 5.如图所示,半圆的直径AB=10,弦CD∥
AB,且∠CAD=30°,则图中阴影部分的面积为 .?则2π·2= ,∴n=120,即∠APA'=120°,则∠APB=60°.连接AB,AD,则△APB为等边三角形.∵D是PB的中点,∴AD⊥PB.∴AD= ,
∴蚂蚁爬行的最短路程为 .利用圆锥的侧面展开图求最短距离如图24 - 137所示,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为 ( )A. B.2 C.3 D.3〔解析〕 如图24 - 138所示,将圆锥的侧面展开,由 的长求∠APA'的度数,设∠APA'的度数为n°,例6C解:如图97所示,将圆锥的侧面展开得到扇形SAA',则这条公路的最短路程是AC'的长.在Rt△OBS中,∵OB=4千米,OS= 千米,∴SB= =16千米,∴SA=16千
米,SC' =8千米, =8π千米.设圆心角∠ASA'的度数为n°,则8π= ,解得n=90,∴∠ASA'=90°.在Rt△ASC'中,AC' = 千米.答:这条公路的最短路程为 千米.6.如图所示,有一座大山,大致呈圆锥形,底面半径为4千米,山高为 千米,在山坡SA中点C处有一联络站,要从山脚A修一盘山路,绕山坡一周将物资运往C处,这条公路的最短路程是多少?图97
同课章节目录
