江西省赣州市第九中学人教版七年级下册数学课件:6.1.1算术平方根(共14张ppt)
文档属性
| 名称 | 江西省赣州市第九中学人教版七年级下册数学课件:6.1.1算术平方根(共14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-13 00:00:00 | ||
图片预览





文档简介
课件14张PPT。
6.1.1算术平方根学习目标:1、了解算术平方根的意义,能运用根号表示一个数的算术平方根
2、了解一个正数的算术平方根与平方互为逆运算,会利用这个互逆运算关系求某些非负数的算术平方根请你说一说解决问题的思路.1.情境导入 学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?小欧还要准备一些面积如下的正方形画布,
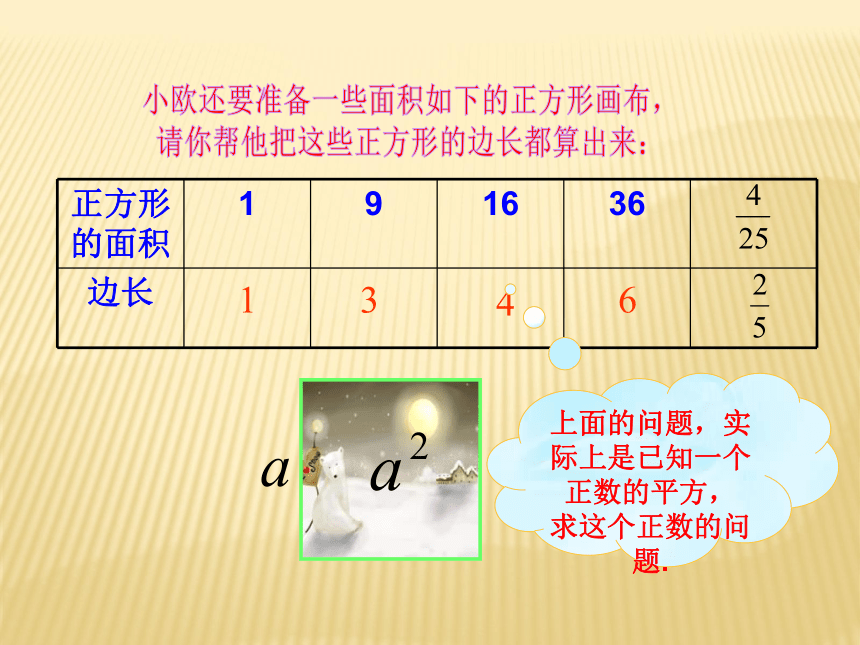
请你帮他把这些正方形的边长都算出来:1346上面的问题,实际上是已知一个正数的平方, 求这个正数的问题.
一般地,如果一个正数x的平方等于a,
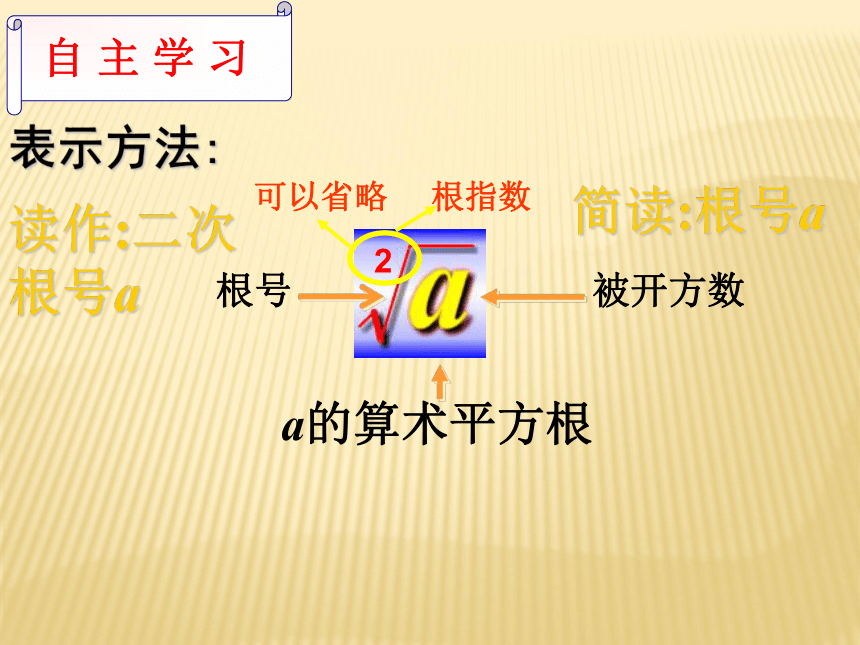
即 ,那么这个正数x叫做a的算术平方根。 a的算术平方根记为:读作:“根号a”,
a叫做被开方数。 算术平方根表示方法:简读:根号a2读作:二次根号a例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,即 =10。(2)因为 = ,所以 的算术平方
根是 ,即 =
(3)因为 =0.0001,所以0.0001的算术平方根为0.01,即 =0.01。其实:求算术平方根的过程就是平方的相反运算思
考 从例1可以看出:被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
从例1可以看出:被开放数越大,对应的算术平方根也越大。这个结论对所有的正数都成立。求下列各数的算数平方根:
(1)81 ; (2)0.0025; (3)32?学生演板1.求下列各式的值:
(1) (2) (3) (4) 解:(1)
(2)
(3)
(4) 巩固与提高2.填空(1) 16的算术平方根是
(2)算术平方根是4的数是
(3) 的算术平方根是
(4) 的算术平方根是
(5) 的算术平方根是( 4 )
(16 )
( 2 )
( 2 )
( )
小结:1.带分数要先化成假分数。
2.表示的意义就是算术平方根。
课堂小结与课后作业小结:1.知识与技能:算术平方根的定义
算术平方根的求法
2.方法与思想: 具体到抽象的数学方法
方程思想
数学建模课后作业:课本第47页第1题(作业本)
小练第14页
大练第35页练习1能拼成正方形吗?你能用两个面积为1的小正方形拼成一个面积为2的大正方形吗?
你能知道大正方形的边长吗? 有多大呢?解 = = 4.求 的值5.120.0013谢
谢
6.1.1算术平方根学习目标:1、了解算术平方根的意义,能运用根号表示一个数的算术平方根
2、了解一个正数的算术平方根与平方互为逆运算,会利用这个互逆运算关系求某些非负数的算术平方根请你说一说解决问题的思路.1.情境导入 学校要举行美术作品比赛,小鸥想裁出一块面积为25 dm2的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?小欧还要准备一些面积如下的正方形画布,
请你帮他把这些正方形的边长都算出来:1346上面的问题,实际上是已知一个正数的平方, 求这个正数的问题.
一般地,如果一个正数x的平方等于a,
即 ,那么这个正数x叫做a的算术平方根。 a的算术平方根记为:读作:“根号a”,
a叫做被开方数。 算术平方根表示方法:简读:根号a2读作:二次根号a例1 求下列各数的算术平方根:
(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的算术平方根为10,即 =10。(2)因为 = ,所以 的算术平方
根是 ,即 =
(3)因为 =0.0001,所以0.0001的算术平方根为0.01,即 =0.01。其实:求算术平方根的过程就是平方的相反运算思
考 从例1可以看出:被开方数的大小与对应的算术平方根的大小之间有什么关系呢?
从例1可以看出:被开放数越大,对应的算术平方根也越大。这个结论对所有的正数都成立。求下列各数的算数平方根:
(1)81 ; (2)0.0025; (3)32?学生演板1.求下列各式的值:
(1) (2) (3) (4) 解:(1)
(2)
(3)
(4) 巩固与提高2.填空(1) 16的算术平方根是
(2)算术平方根是4的数是
(3) 的算术平方根是
(4) 的算术平方根是
(5) 的算术平方根是( 4 )
(16 )
( 2 )
( 2 )
( )
小结:1.带分数要先化成假分数。
2.表示的意义就是算术平方根。
课堂小结与课后作业小结:1.知识与技能:算术平方根的定义
算术平方根的求法
2.方法与思想: 具体到抽象的数学方法
方程思想
数学建模课后作业:课本第47页第1题(作业本)
小练第14页
大练第35页练习1能拼成正方形吗?你能用两个面积为1的小正方形拼成一个面积为2的大正方形吗?
你能知道大正方形的边长吗? 有多大呢?解 = = 4.求 的值5.120.0013谢
谢
