云南省绿春县大水沟中学人教版七年级下册数学课件:6.3实数(第一课时)
文档属性
| 名称 | 云南省绿春县大水沟中学人教版七年级下册数学课件:6.3实数(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-13 21:47:00 | ||
图片预览






文档简介
课件16张PPT。6.3 实数
(第1课时) 本节先将有理数与有限小数和无限循环小数统一起来,再采用与有理数对照的方法引入无理数,接着类比用数轴上的点表示有理数,指出实数与数轴上的点的一一对应关系.课件说明学习目标:
(1)了解无理数和实数的概念.
(2)知道实数与数轴上的点具有一一对应关系,初步体会“数形结合”的数学思想.
学习重点:
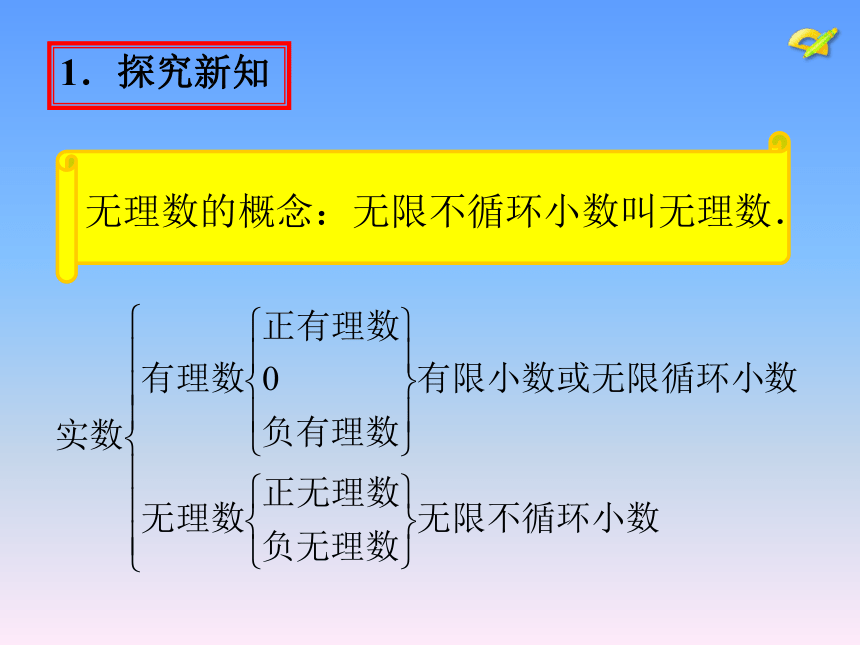
了解无理数和实数的概念,知道实数与数轴上的点的一一对应关系.课件说明1.探究新知有理数包括整数和分数,如果将下列分数写成小数的形式,你有什么发现?1.探究新知你认为小数除了上述类型外,还会有什么类型的小数?1.探究新知无理数的概念:无限不循环小数叫无理数.1.探究新知因为非零有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗? 5,3.14,0, , , , ,- π,
0.1010010001……(相邻两个1之间0的个数逐次加1).1.探究新知例1 下列实数中,哪些是有理数?哪些是无理数?1.探究新知我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?1.探究新知直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?2.运用新知判断正误,并说明理由.
(1)无理数都是无限小数;
(2) 实数包括正实数、0、负实数;
(3)不带根号的数都是有理数;
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.2.运用新知把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.2.运用新知练习1 下列各数中,哪些是有理数?哪些是无理数?2.运用新知练习2
在下列每一个圈里,至少填入三个适当的数.3.归纳总结问题1 举例说明有理数和无理数的特点是什么?
问题2 实数是由哪些数组成的?
问题3 实数与数轴上的点有什么关系?4.布置作业教科书 习题 6.3 第1、2题;
教科书 复习题 6 第6题.
(1)了解无理数和实数的概念.
(2)知道实数与数轴上的点具有一一对应关系,初步体会“数形结合”的数学思想.
学习重点:
了解无理数和实数的概念,知道实数与数轴上的点的一一对应关系.课件说明1.探究新知有理数包括整数和分数,如果将下列分数写成小数的形式,你有什么发现?1.探究新知你认为小数除了上述类型外,还会有什么类型的小数?1.探究新知无理数的概念:无限不循环小数叫无理数.1.探究新知因为非零有理数和无理数都有正负之分,那么你能类比有理数的分类方法,按大小关系对实数分类吗? 5,3.14,0, , , , ,- π,
0.1010010001……(相邻两个1之间0的个数逐次加1).1.探究新知例1 下列实数中,哪些是有理数?哪些是无理数?1.探究新知我们知道,每个有理数都可以用数轴上的点来表示,那么无理数是否也可以用数轴上的点表示出来呢?你能在数轴上找到表示无理数的点吗?1.探究新知直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O,点O' 对应的数是多少?2.运用新知判断正误,并说明理由.
(1)无理数都是无限小数;
(2) 实数包括正实数、0、负实数;
(3)不带根号的数都是有理数;
(4)所有有理数都可以用数轴上的点表示, 反过来,数轴上所有的点都表示有理数.2.运用新知把下列各数填入相应的集合内:
①有理数集合:{ …};
②无理数集合:{ …};
③正实数集合:{ …};
④负实数集合:{ …}.2.运用新知练习1 下列各数中,哪些是有理数?哪些是无理数?2.运用新知练习2
在下列每一个圈里,至少填入三个适当的数.3.归纳总结问题1 举例说明有理数和无理数的特点是什么?
问题2 实数是由哪些数组成的?
问题3 实数与数轴上的点有什么关系?4.布置作业教科书 习题 6.3 第1、2题;
教科书 复习题 6 第6题.
