1.2 独立性检验的基本思想及其初步应用 课件3
文档属性
| 名称 | 1.2 独立性检验的基本思想及其初步应用 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 305.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-12 00:00:00 | ||
图片预览





文档简介
课件15张PPT。1.2独立性检验的基本思想
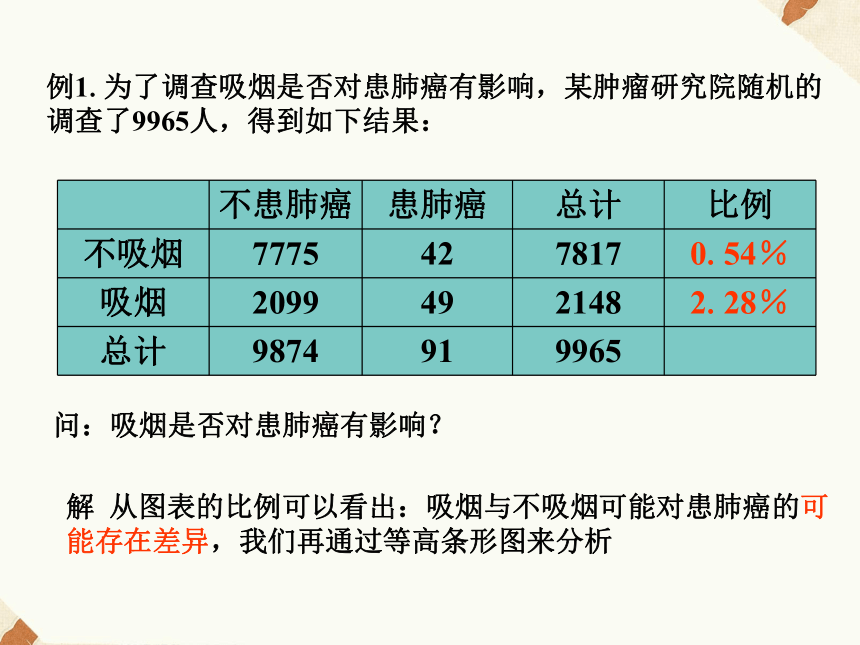
及其初步应用前面我们讨论了两个变量之间的关系——回归分析,以及对分析了解释变量和随机误差对预报变量的影响的强弱分析——相关指数R2分析事实上,对于同一个总体而言,通过对比更能得出哪一种方法或哪个变量对总体效果有较大的影响,分类变量间的关系就是我们今天要研究的变量属于不同的类别例1.为了调查吸烟是否对患肺癌有影响,某肿瘤研究院随机的调查了9965人,得到如下结果:问:吸烟是否对患肺癌有影响?解 从图表的比例可以看出:吸烟与不吸烟可能对患肺癌的可能存在差异,我们再通过等高条形图来分析等高条形图不吸烟上面我们通过图形的分析,初步判断吸烟与患肺癌有关系.那么,事实是否如此呢?我们需要用统计的观点来考察这个问题我们首先设基本事件为:H0:吸烟与患肺癌没有关系我们下面就一般关系做一个推断如果吸烟与患肺癌没有关系,则:a(c+d)≈c(a+b)ad-bc≈0因此,| ad-bc |越小,说明吸烟与患肺炎之间没有关系.为了使样本空间有一定的代表性,我们引入一个随机变量(n=a+b+c+d(样本容量))若,H0成立,(吸烟与患肺癌无关)则K应该很小,通过计算我们可以得到K的观测值:
k=K2=56.632总计的四项说明:根据统计学家的分析:
P(K2≥6.635)≈0.01表1-12k>2.706,就有90%的把握认为X与Y之间存在关系有统计规律可以看出:K2=6.635的概率非常小,近似于0.01,也就是说,在H0成立的概率为1%,即H0不成立的概率为99%,因此我们认为吸烟与患肺癌有关上面的利用K2来检验“两个变量有关系”的方法成为:独立性检验说明:两个变量X与Y独立性检验的一般方法:1.设两个变量的值域分别为{x1,x2}{y1.,y2},列频数关联表3.利用统计概率表1-12查阅发生的概率2.计算变量X与Y的评判标准K24.得出概率结论例1.某心脏病医院为了研究秃顶是否与心脏病有关,对665名男性心脏和772名其他病人做了研究,如图所示:智慧的闪光! 不秃头K2=16.373K2=16.373>10.828因此,在犯错误概率不超过0.010的前提下,认为秃头与心脏病有关.研究人员表示,掉头发在很大程度上是由日渐增大的工作压力、不能充分休息、不正确饮食和睡眠不足等因素引起的.在接受调查的人群中,有41%的受秃头威胁的人表示,他们一日睡觉时间不足4小时 秃顶=心脏病?练习1.统计班上一次数学考试,分析男生与女生的成绩,在多大程度上认为男生的数学成绩优于女生的数学成绩?为什么?2.调查我校男女生对理科的偏好,在多大程度上可以认为男生比女生喜欢理科课程?为什么?
及其初步应用前面我们讨论了两个变量之间的关系——回归分析,以及对分析了解释变量和随机误差对预报变量的影响的强弱分析——相关指数R2分析事实上,对于同一个总体而言,通过对比更能得出哪一种方法或哪个变量对总体效果有较大的影响,分类变量间的关系就是我们今天要研究的变量属于不同的类别例1.为了调查吸烟是否对患肺癌有影响,某肿瘤研究院随机的调查了9965人,得到如下结果:问:吸烟是否对患肺癌有影响?解 从图表的比例可以看出:吸烟与不吸烟可能对患肺癌的可能存在差异,我们再通过等高条形图来分析等高条形图不吸烟上面我们通过图形的分析,初步判断吸烟与患肺癌有关系.那么,事实是否如此呢?我们需要用统计的观点来考察这个问题我们首先设基本事件为:H0:吸烟与患肺癌没有关系我们下面就一般关系做一个推断如果吸烟与患肺癌没有关系,则:a(c+d)≈c(a+b)ad-bc≈0因此,| ad-bc |越小,说明吸烟与患肺炎之间没有关系.为了使样本空间有一定的代表性,我们引入一个随机变量(n=a+b+c+d(样本容量))若,H0成立,(吸烟与患肺癌无关)则K应该很小,通过计算我们可以得到K的观测值:
k=K2=56.632总计的四项说明:根据统计学家的分析:
P(K2≥6.635)≈0.01表1-12k>2.706,就有90%的把握认为X与Y之间存在关系有统计规律可以看出:K2=6.635的概率非常小,近似于0.01,也就是说,在H0成立的概率为1%,即H0不成立的概率为99%,因此我们认为吸烟与患肺癌有关上面的利用K2来检验“两个变量有关系”的方法成为:独立性检验说明:两个变量X与Y独立性检验的一般方法:1.设两个变量的值域分别为{x1,x2}{y1.,y2},列频数关联表3.利用统计概率表1-12查阅发生的概率2.计算变量X与Y的评判标准K24.得出概率结论例1.某心脏病医院为了研究秃顶是否与心脏病有关,对665名男性心脏和772名其他病人做了研究,如图所示:智慧的闪光! 不秃头K2=16.373K2=16.373>10.828因此,在犯错误概率不超过0.010的前提下,认为秃头与心脏病有关.研究人员表示,掉头发在很大程度上是由日渐增大的工作压力、不能充分休息、不正确饮食和睡眠不足等因素引起的.在接受调查的人群中,有41%的受秃头威胁的人表示,他们一日睡觉时间不足4小时 秃顶=心脏病?练习1.统计班上一次数学考试,分析男生与女生的成绩,在多大程度上认为男生的数学成绩优于女生的数学成绩?为什么?2.调查我校男女生对理科的偏好,在多大程度上可以认为男生比女生喜欢理科课程?为什么?
