2.1.2 演绎推理 课件3

课件50张PPT。2.1.2　
演绎推理1.演绎推理
(1)含义:从一般性的原理出发，推出某个_________下的结论，我们把这种推理称为演绎推理.
(2)特点:演绎推理是由_____到_____的推理.特殊情况一般特殊2.三段论已知的一般原理所研究的特殊情况特殊情况1.判一判(正确的打“√”，错误的打“×”)
(1)“三段论”就是演绎推理.　(　　)
(2)演绎推理的结论是一定正确的.　(　　)
(3)演绎推理是由特殊到一般再到特殊的推理.　(　　)【解析】(1)错误.“三段论”是演绎推理的一般模式，却不是演绎推理.
(2)错误.在演绎推理中，只有“大前提”“小前提”及推理形式都正确的情况下，其结论才是正确的.
(3)错误.演绎推理是由一般到特殊的推理.
答案:(1)×　(2)×　(3)×2.做一做(请把正确的答案写在横线上)
(1)用演绎推理证明“y=sinx是周期函数”时的大前提是　　　　　　　　　　　，小前提是　　　　　　　　　.
(2)正弦函数是奇函数，f(x)=sin(x2+1)是正弦函数，因此
f(x)=sin(x2+1)是奇函数，以上推理中“三段论”中的
　　　　是错误的.
(3)推理某一“三段论”，其前提之一为肯定判断，结论为否定判断，且推理形式正确，由此可以推断，该三段论的另一前提必为　　　　判断(选填“肯定”或“否定”)【解析】2.(1)y=sinx是三角函数，而三角函数是周期函数，因此大前提为三角函数为周期函数、小前提应该为y=sinx是三角函数.
答案:三角函数是周期函数　y=sinx是三角函数
(2)小前提错误.因为f(x)=sin(x2+1)不是正弦函数.
答案:小前提
(3)演绎推理在大、小前提和推理形式都正确的前提下，得到结论一定正确.
答案:否定【要点探究】
知识点 演绎推理
1.演绎推理的三个特点
(1)演绎推理的前提是一般性原理，演绎推理所得的结论是蕴涵于前提之中的个别、特殊事实，结论完全蕴涵于前提之中.
(2)在演绎推理中，前提与结论之间存在必然的联系，只要前提是真实的，推理的形式是正确的，那么结论也必定是正确的.因而演绎推理是数学中严格证明的工具.
(3)演绎推理是由一般到特殊的推理.2.对“三段论”的三点说明
(1)三段论中的大前提提供了一个一般性原理，小前提指出了一种特殊情况，两个命题结合起来，揭示了一般性原理与特殊情况的内在联系，从而得到了第三个命题——结论.
(2)若集合M的所有元素都具有性质P，S是M中的一个子集，那么S中的元素也具有性质P；若M中的元素都不具有性质P，则S中的元素也不具有性质P.
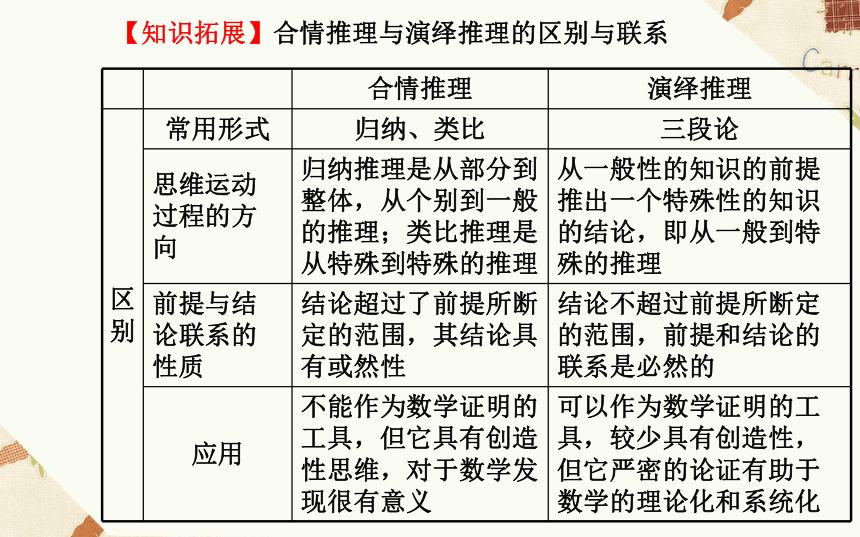
(3)从以上两点可以看出:三段论推理的结论正确与否，取决于两个前提是否正确，推理形式(即S与M的包含关系)是否正确.【知识拓展】合情推理与演绎推理的区别与联系【微思考】
合情推理与演绎推理的作用分别是什么？
提示:合情推理的作用是探索方法，寻求思路，发现规律，得到猜想，而演绎推理的作用在于对由合情推理得到的结论，进行严格的证明.【即时练】
1.已知幂函数f(x)=xα是增函数，而
y=x-1是幂函数，所以y=x-1是增函数，上面推理错误是(　　)
A.大前提错误导致结论错
B.小前提错误导致结论错
C.推理的方式错误导致错
D.大前提与小前提都错误导致错
【解析】选A.大前提为:f(x)=xα是增函数，在f(x)=xα中当α>0时f(x)为增函数，显然大前提是错误的.2.函数y=2x+5的图象是一条直线，用三段论表示为:
大前提　　　　　　　　　　　　　　　　　　　　　　.
小前提　　　　　　　　　　　　　　　　　　　　　　.
结论　　　　　　　　　　　　　　　　　　　　　　　.【解析】根据三段论模式分析题意可知:
一次函数y=kx+b(k≠0)的图象是一条直线，…大前提
y=2x+5是一次函数，…小前提
函数y=2x+5的图象是一条直线.…结论
答案:一次函数y=kx+b(k≠0)的图象是一条直线
y=2x+5是一次函数
函数y=2x+5的图象是一条直线 【题型示范】
类型一 用三段论证明几何问题
【典例1】
(1)推理:“①矩形是平行四边形；
②正方形是矩形；③所以正方形是平行四边形”中的小前提是　　　.
(2)证明:如果梯形的两腰和一底相等，那么它的对角线必平分另一底上的两个角.【解题探究】1.题(1)中的推理是什么形式？
2.题(2)中证明的方法和步骤是什么？
【探究提示】1.题中的推理是三段论的形式.
2.先将文字语言转化为几何语言，利用平行线的性质去寻求角的关系.【自主解答】(1)推理:“①矩形是平行四边形，②正方形是矩形，③所以正方形是平行四边形”中:
矩形是平行四边形，………………………………………大前提
正方形是矩形，……………………………………………小前提
所以正方形是平行四边形.………………………………结论
答案:②(2)已知在梯形ABCD中(如图所示)，
AB=DC=AD，AC和BD是它的对角线，
求证:CA平分∠BCD，BD平分∠CBA.
证明:①等腰三角形的两底角相等，…………………大前提
△DAC是等腰三角形，DC=DA，…………………………小前提
∠1=∠2.………………………………………………结论
②两条平行线被第三条直线所截，内错角相等，……大前提
∠1和∠3是平行线AD，BC被AC所截的内错角，………小前提
∠1=∠3.………………………………………………结论③等于同一个量的两个量相等，………………………大前提
∠2，∠3都等于∠1，……………………………………小前提
∠2和∠3相等.…………………………………………结论
即CA平分∠BCD.
④同理BD平分∠CBA.【方法技巧】
1.用三段论证明命题的步骤
(1)理清楚证明命题的一般思路.
(2)找出每一个结论得出的原因.
(3)把每个结论的推出过程用“三段论”表示出来.2.三段论中的三个判断
三段论是由三个判断组成的，其中的两个为前提，另一个为结论.
第一个判断是提供性质的一般判断，叫做大前提，通常是已知的公理、定理、定义等；
第二个判断是和大前提有联系的特殊情况，叫做小前提，通常是已知条件或前面证明过程中推理的第三个判断；
第三个判断为结论.
在推理论证的过程中，一个稍复杂一点的证明题经常要由几个三段论才能完成，而大前提通常省略不写，或者写在结论后面的括号内，小前提有时也可以省去，而采取某种简明的推理格式.【变式训练】如图，△ABC中，D，E，F分别是BC，CA，AB上的点，∠BFD=∠A，DE∥BA.求证ED=AF，写出“三段论”形式的演绎推理.【解题指南】只需证明四边形AEDF为平行四边形即可.【证明】因为同位角相等，两直线平行，………………大前提
∠BFD与∠A是同位角，且∠BFD=∠A，…………………小前提
所以FD∥AE.……………………………………………结论
因为两组对边分别平行的四边形是平行四边形，
……………………………………………………………大前提
DE∥BA，且FD∥AE，………………………………………小前提
所以四边形AFDE为平行四边形.…………………………结论
因为平行四边形的对边相等，…………………………大前提
ED和AF为平行四边形AFDE的对边，……………………小前提
所以ED=AF.………………………………………………结论【补偿训练】已知在空间四边形ABCD中，点E，F分别是AB，AD的中点，如图所示，求证:EF∥平面BCD(指出大前提，小前提及结论).【证明】因为三角形中位线与第三边平行，…………大前提
点E，F分别是AB，AD的中点，EF是△ABD的中位线，
…………………………………………………………小前提
所以EF∥BD.……………………………………………结论
因为平面外一条直线与平面内一条直线平行，则该直线与平
面平行，…………………………………………………大前提
EF?平面BCD，BD?平面BCD，EF∥BD，…………………小前提
所以EF∥平面BCD.……………………………………结论类型二 演绎推理在代数证明中的应用
【典例2】
(1)由“(a2+a+1)x>3，得x> ”
的推理过程中，其大前提是　　　　　.
(2)已知函数f(x)=ax+ (a>1)，证明:函数f(x)在(-1，+∞)
上为增函数.【解题探究】1.题(1)中的大前提怎样找？
2.题(2)中证明的方法是什么？
【探究提示】1.将推理过程写成三段论的形式.
2.利用增函数的定义或利用f′(x)>0证明.【自主解答】(1)该推理过程写成三段论形式:
不等式两边同除以一个正数，不等号的方向不变，…大前提
(a2+a+1)x>3，a2+a+1大于0，…………………………小前提
x> .…………………………………………结论
答案:不等式两边同除以一个正数，不等号方向不变(2)方法一:(定义法)任取x1，x2∈(-1，+∞)，
且x10，且a>1，所以 >1.
而-1所以x1+1>0，x2+1>0，
所以f(x2)-f(x1)>0，
所以f(x)在(-1，+∞)上为增函数.方法二:(导数法)f(x)=
所以f′(x)=axlna+ .
因为x>-1，所以(x+1)2>0，所以 >0.
又因为a>1，所以lna>0，ax>0，
所以axlna>0.所以f′(x)>0.
于是得f(x)=ax+ 在(-1，+∞)上是增函数.【方法技巧】代数问题中的常见的利用三段论证明的命题
(1)函数类问题:比如函数的单调性、奇偶性、周期性和对称性等.
(2)导数的应用:利用导数研究函数的单调区间，求函数的极值和最值，证明与函数有关的不等式等.
(3)三角函数的图象与性质.
(4)数列的通项公式、递推公式以及求和，数列的性质.
(5)不等式的证明.【变式训练】证明f(x)=x3+x在R上为增函数，并指出证明过程中所运用的“三段论”.【证明】在R上任取x1，x2，且x10.
因为f(x)=x3+x，
所以f(x2)-f(x1)=( +x2)-( +x1)
=( - )+(x2-x1)
=(x2-x1)( +x2x1+ +1)
=(x2-x1)·因为
所以f(x2)-f(x1)>0，即f(x2)>f(x1)，
所以f(x)=x3+x在R上是增函数.
在证明过程中所用到的“三段论”:大前提是“增函数的定义”，小前提是“题中的f(x)经过正确的推理满足增函数的定义”，结论是“f(x)是增函数”.【补偿训练】已知数列{an}满足a1=1，a2=3，an+2=3an+1-2an(n∈N*).
(1)证明:数列{an+1-an}是等比数列.
(2)求数列{an}的通项公式.【解析】(1)因为an+2=3an+1-2an，
所以an+2-an+1=2an+1-2an=2(an+1-an)，
所以 =2(n∈N*)而a2-a1=2.
所以数列{an+1-an}是以2为首项，2为公比的等比数列.
(2)an=(an-an-1)+(an-1-an-2)+…(a3-a2)+(a2-a1)+a1
=2n-1+2n-2+…22+21+1
= +1
=2n-1.【拓展类型】拓展类型演绎推理与合情推理的关系
【备选典例】
1.下列推理过程是演绎推理的为(　　)
A.人们通过大量试验得出抛硬币出现正面的概率为
B.科学家通过研究老鹰的眼睛发明了电子鹰眼
C.我们由a1=1，a2=3，a3=5，…推测得an=2n-1(n∈N*)
D.数学中由周期函数的定义判断某函数是否为周期函数
2.用三段论写出求解下题的主要解答过程.
若不等式|ax+2|<6的解集为(-1，2)，求实数a的值.【解析】1.选D.根据题意，对于A人们通过大量试验得出抛硬
币出现正面的概率为 ，这是归纳推理.
B.科学家通过研究老鹰的眼睛发明了电子鹰眼，根据其原理来制造相同的物体，这是类比推理.
C.由a1，a2，a3，…归纳得出an的通项，是归纳推理.
D.数学中由周期函数的定义判断某函数是否为周期函数，是演绎推理，故选D.2.推理的第一个关键环节:
大前提:如果不等式f(x)<0的解集为(m，n)，且f(m)，f(n)有意义，则m，n是方程f(x)=0的实数根，
小前提:不等式|ax+2|<6的解集为(-1，2)，
且x=-1与x=2都使表达式|ax+2|-6有意义，
结论:-1和2是方程|ax+2|-6=0的根.所以|-a+2|-6=0与|2a+2|-6=0同时成立.
推理的第二个关键环节:
大前提:如果|x|=a，a>0，那么x=±a，
小前提:|-a+2|=6且|2a+2|=6，
结论:-a+2=±6且2a+2=±6.
可得出结论a=-4.【方法技巧】应用演绎推理的一般思路
　　在运用演绎推理，即三段论证明问题时要充分挖掘题目外在和内在条件(小前提)，根据需要引入相关的适用的定理和性质(大前提)，并保证每一步的推理都是正确的、严密的，才能得出正确的结论.【易错误区】忽略大前提而致误
【典例】已知2sin2α+sin2β=3sinα，则sin2α+sin2β的取值范围为　　　　　.【解析】由2sin2α+sin2β=3sinα
得sin2α+sin2β=-sin2α+3sinα
因为0≤sin2β≤1，sin2β=3sinα-2sin2α，
所以0≤3sinα-2sin2α≤1.
解之得sin α=1②或0≤sinα≤ ，
令y=sin2α+sin2β，当sinα=1时，y=2.
当0≤sinα≤ 时，0≤y≤ .
所以sin2α+sin2β的取值范围是[0， ]∪{2}.
答案:[0， ]∪{2}【常见误区】【防范措施】
1.正确理解大前提
解题过程中，要对大前提把握好，正确认识大前提是解题的关键，如本例中sinα的取值范围.
2.挖掘题中的隐含条件
解题时要对题目中的隐含条件挖掘到位，不能遗漏，否则会出现失误，如本例中sinα=1易漏掉.【类题试解】设α，β，γ∈(0， )，且tan α=
tan β= tan γ= 则α+β+γ=_____.【解析】tan(α+β)=
由tan α= 且α∈(0， )得0＜α＜ ，tan β=
知β∈(0， ).
由tan γ= 得γ∈(0， )，所以α+β+γ∈(0， )，
所以α+β+γ= .
答案：