2.2.1 综合法 课件
图片预览











文档简介
课件45张PPT。2.2 直接证明与间接证明
2.2.1 综合法和分析法
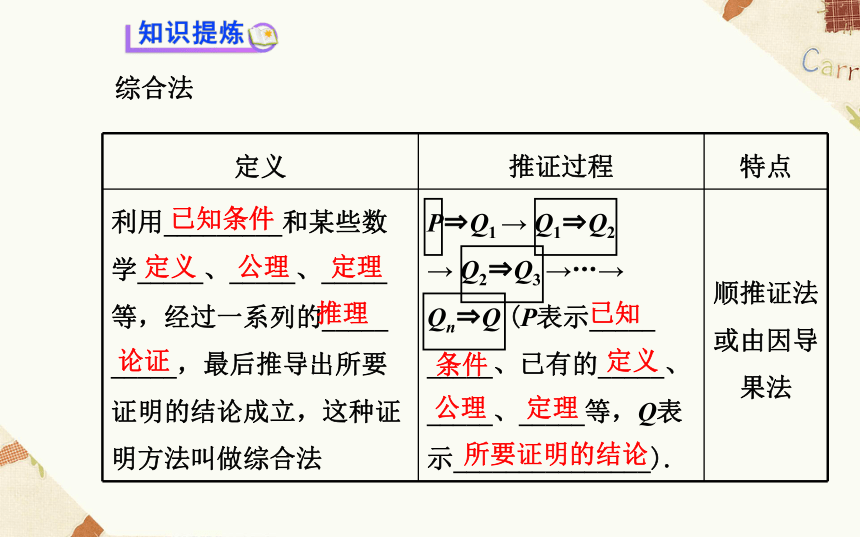
第1课时 综 合 法综合法 已知条件定义公理定理推理论证已知条件定义公理定理所要证明的结论1.判一判(正确的打“√”,错误的打“×”)
(1)综合法是执果索因的逆推证法.( )
(2)综合法证明的依据是三段论.( )
(3)综合法的推理过程实际上是寻找它的必要条件.( )【解析】(1)错误.综合法是一种由因导果的顺推证法.
(2)正确.综合法的逻辑依据是三段论.
(3)正确.综合法从“已知”看“可知”,逐步推出“未知”,其逐步推理实际上是寻找它的必要条件.
答案:(1)× (2)√ (3)√2.做一做(请把正确的答案写在横线上)
(1)已知函数f(x)=ax2+bx+c是偶函数,则b的值为 .
(2)在不等式“a2+b2≥2ab”的证明中:因为a2+b2-2ab=(a-b)2≥0所以a2+b2≥2ab,该证明用的方法是 .
(3)角A,B为△ABC内角,A>B是sinA>sinB的 条件(填“充分”“必要”“充要”或“既不充分又不必要”).【解析】(1)由于f(x)为偶函数.所以f(-x)=f(x).
所以ax2-bx+c=ax2+bx+c,
所以-bx=bx,所以b=0.
答案:0
(2)由因导果,易知该证法为综合法.
答案:综合法
(3)角A,B为△ABC内角且A>B,所以sinA>sinB,由sinA>sinB(A,B均为△ABC的内角)知A>B.
答案:充要【要点探究】
知识点 综合法
1.综合法的基本思路
综合法的基本思路是“由因导果”,由已知走向求证,即从数学题的已知条件出发,经过逐步的逻辑推理,最后导出待证结论或需求的问题.2.综合法的两个特点
(1)用综合法证明不等式,证明步骤严谨,逐层递进,步步为营,条理清晰,形式简洁,宜于表达推理的思维轨迹.
(2)因用综合法证明命题“若A则D”的思考过程可表示为:故要从A推理到D,由A推演出的中间结论未必唯一,如B,B1,B2等,可由B,B1,B2进一步推演出的中间结论则可能更多,如C,C1,C2,C3,C4等等.
所以如何找到“切入点”和有效的推理途径是有效利用综合法证明问题的“瓶颈”. 【知识拓展】综合法证明不等式时常用的不等式
(1)a2+b2≥2ab(当且仅当a=b时取等号).
(2) (a,b∈R*,当且仅当a=b时取等号).
(3)a2≥0,|a|≥0,(a-b)2≥0.
(4) ≥2(a,b同号). ≤-2(a,b异号).
(5)a,b∈R,a2+b2≥ (a+b)2.(6)不等式的性质
定理1 对称性:a>b?b定理2 传递性: ?a>c.
定理3 加法性质: ?a+c>b+c.
推论 ?a+c>b+d.
定理4 乘法性质: ?ac>bc.
推论1 ?ac>bd.
推论2 ?an>bn.
定理5 开方性质:【微思考】
综合法的推理过程是合情推理还是演绎推理?
提示:综合法的推理过程是演绎推理,它的每一步推理都是严密的逻辑推理,得到的结论是正确的.【即时练】
1.下面的四个不等式:①a2+b2+3≥
ab+ (a+b);②a(1-a)≤ ;③ ≥2;④(a2+b2)·
(c2+d2)≥(ac+bd)2,其中恒成立的有 .
2.求证:a2+b2+c2≥ab+ac+bc.【解析】1.因为a2+b2≥2ab,a2+3≥2 a,b2+3≥2 b.相加
得2(a2+b2+3)≥2ab+2 (a+b),所以a2+b2+3≥ab+ (a+b),
所以①正确.由于a(1-a)- =-a2+a- =- ≤0.所以
②正确.(a2+b2)·(c2+d2)=a2c2+a2d2+b2c2+b2d2≥a2c2+2abcd+
b2d2=(ac+bd)2,所以④正确.而 ≥2,因为a,b的符号不确定,所以不一定成立.
答案:①②④2.因为a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc.
将此三式相加可得
2(a2+b2+c2)≥2ab+2ac+2bc,所以a2+b2+c2≥ab+ac+bc,
所以原式成立. 【题型示范】
类型一 用综合法证明三角问题
【典例1】
(1)在△ABC中,已知cosAcosB>sinAsinB,则△ABC的形状一定是 .
(2)在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=
(2b-c)sinB+(2c-b)sinC.
①求证:A的大小为60°;
②若sinB+sinC= .证明△ABC为等边三角形.【解题探究】1.题(1)中△ABC的形状可从哪些角度判断?
2.题(2)中①A的大小怎样与已知条件联系起来?②中怎样说明△ABC为等边三角形?
【探究提示】1.可以从边的角度或角的角度判断△ABC的形状,结合已知条件应从角的角度判断.
2.①中可利用正弦定理将角与边互化然后利用余弦定理求A;
②中由sinB+sinC= 及隐含条件A=60°可求B,C,说明△ABC的形状.【自主解答】(1)因为cosAcosB>sinAsinB,
所以cosAcosB-sinAsinB
=cos(A+B)>0.
因为0又C=π-(A+B),所以C∈
即△ABC为钝角三角形.
答案:钝角三角形(2)①由2asinA=(2b-c)sinB+(2c-b)sinC,
得2a2=(2b-c)·b+(2c-b)c,
即bc=b2+c2-a2,
所以cosA=
所以A=60°.②由A+B+C=180°得B+C=120°,
由sin B+sin C= 得sin B+sin(120°-B)=
sin B+(sin 120°cos B-cos 120°sin B)=
sin B+ cos B=
即sin(B+30°)=1.
因为0°<B<120°,
所以30°<B+30°<150°,
所以B+30°=90°,即B=60°,
所以A=B=C=60°.
即△ABC为等边三角形.【方法技巧】
1.综合法处理问题的三个步骤2.证明三角等式的主要依据
(1)三角函数的定义、诱导公式及同角基本关系式.
(2)和、差、倍角的三角函数公式.
(3)三角形中的三角函数及三角形内角和定理.
(4)正弦定理、余弦定理和三角形的面积公式.【变式训练】已知a,b,c为△ABC的三边,x∈R,求证:方程a2x2+(b2-a2-c2)x+c2=0没有实数根.【证明】已知a,b,c为△ABC的三边,x∈R,和方程a2x2+(b2-a2-c2)x+c2=0.
根据根的判别式可知:Δ=(b2-a2-c2)2-4a2c2
=(b2-a2-c2+2ac)(b2-a2-c2-2ac)
=(b-a+c)(b+a-c)(b-a-c)(b+a+c),
又因为a,b,c是△ABC的三边,
故b-a+c>0,b+a-c>0,b-a-c<0,b+a+c>0.
所以Δ=(b-a+c)(b+a-c)(b-a-c)(b+a+c)<0,
故方程a2x2+(b2-a2-c2)x+c2=0没有实数根.【补偿训练】求证:sin3α=3sinα-4sin3α.
【解析】左边=sin(2α+α)
=sin2αcosα+cos2αsinα
=2sinαcos2α+(1-2sin2α)sinα
=2sinα(1-sin2α)+sinα-2sin3α
=2sinα-2sin3α+sinα-2sin3α
=3sinα-4sin3α=右边.
所以sin3α=3sinα-4sin3α.类型二 综合法在数列中的应用
【典例2】
(1)已知方程(x2-mx+2)(x2-nx+2)=0的四个根组成一个首项为 的等比数列,则|m-n|= .(2)设数列{an}的前n项和为Sn,满足(3-m)Sn+2man=m+3(n∈N*).其中m为常数,且m≠-3,m≠0.
①求证:{an}是等比数列.
②若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=
f(bn-1)(n∈N*,n≥2),求证:{ }为等差数列.【解题探究】1.题(1)中m,n的值怎样求解?
2.题(2)①中证明等比数列的关键是什么?②中怎样说明为
{ }等差数列?
【探究提示】1.利用根与系数的关系结合等比数列的性质可求m,n.
2.①中关键是利用an+1与Sn和Sn+1之间的关系结合等比数列的
定义;②中利用定义说明,即 常数(n≥2).【自主解答】(1)方程(x2-mx+2)(x2-nx+2)=0?x2-mx+2=0①
或x2-nx+2=0②.设方程①两根为x1,x4,方程②两根为x2,x3.
则x1·x4=2,x1+x4=m,x2·x3=2,x2+x3=n.因为方程(x2-mx+2)
(x2-nx+2)=0的四个根组成一个首项为 的等比数列.所以
x1,x2,x3,x4分别为此数列的前四项且x1= ,x4= =4,公比
为2,所以x2=1,x3=2,所以m=x1+x4= +4= ,n=x2+x3=1+2=3,
故|m-n|=
答案:(2)①由(3-m)Sn+2man=m+3,得(3-m)Sn+1+2man+1=m+3,两式相减得(3+m)an+1=2man,
因为m≠0且m≠-3,
所以
所以{an}是等比数列.
②因为b1=a1=1,q=f(m)=
所以n∈N*且n≥2时,
所以{ }是以1为首项, 为公差的等差数列.【延伸探究】题(2)①中若m=1试求{an}的前n项和.
【解析】若m=1则
由已知得(3-1)S1+2a1=4,
所以a1=1,
即数列{an}是以1为首项为 公比的等比数列.
=2-21-n.【方法技巧】综合法证明数列问题的依据【变式训练】在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn= ,求证数列{bn}是等差数列.
(2)求数列{an}的前n项和Sn.
【解题指南】用综合法证明有关数列的问题,同时要注意理解等差数列的含义.【解析】(1)因为an+1=2an+2n,
所以
因为bn=
所以bn+1= =bn+1,
所以数列{bn}是等差数列,其中b1=1,公差为1,
所以bn=n,an=n·2n-1.(2)因为Sn=1×20+2×21+…+(n-1)·2n-2+n·2n-1,
所以2Sn=1×21+2×22+…+(n-1)·2n-1+n·2n,
两式相减得Sn=n·2n-1×20-1×21-…-1×2n-1
=n·2n-2n+1=2n(n-1)+1.【补偿训练】在等比数列{an}中,首项a1>1,公比q>0,n∈N,且n>1.求证lgan+1lgan-1<(lgan)2.【证明】因为{an}为等比数列,
所以 =an-1·an+1(n>1).
又因为a1>1,公比q>0,n∈N,且n>1,
所以lgan-1lgan+1<
所以lgan+1lgan-1<(lgan)2.【规范解答】综合法在几何证明中的应用
【典例】(12分)如图,在四棱锥O-ABCD中,
底面ABCD为菱形,OA⊥平面ABCD,E为OA的
中点,F为BC的中点,求证:
(1)平面BDO⊥平面ACO.
(2)EF∥平面OCD.【审题】抓信息,找思路【点题】警误区,促提升
失分点1:证明时忽略①处条件的运用导致无法证明面面垂直,考试时最多得2分.
失分点2:证明时不能正确地构造出平行四边形,从而无法得到线线平行如本题中②则会导致第(2)问无法证出,实际考试中最多得8分.【悟题】提措施,导方向
1.关注题中的条件
证明时要注意应用题中的条件,注意隐含条件的挖掘,如果漏掉某一条件或对某一条件挖掘不深则会导致题目无法证明,如本例中ABCD为菱形的条件.
2.注重定理的应用
几何证明的前提是熟练地应用各个判定定理及性质定理,注意各个定理的应用格式,掌握常见的辅助线的作法,寻找好定理所需的条件,如本例中构造平行四边形说明线线平行.【类题试解】如图,正方形ABCD和四边形ACEF所在的平面互
相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
(1)求证:AF∥平面BDE.
(2)求证:CF⊥平面BDE.【证明】(1)设AC与BD的交点是G.因为EF∥AG,且EF=1,
AG= AC=1,
所以四边形AGEF为平行四边形,所以AF∥EG,因为EG?平面BDE,AF?平面BDE,
所以AF∥平面BDE.(2)连接FG,因为EF∥CG,EF=CG=1,所以四边形CEFG为平行四边形,
又因为CE=EF=1,所以四边形CEFG为菱形,所以EG⊥CF.
在正方形ABCD中,AC⊥BD.
因为正方形ABCD和四边形ACEF所在的平面互相垂直,
所以BD⊥平面CEFG,
所以BD⊥CF,又因为EG∩BD=G,所以CF⊥平面BDE.
2.2.1 综合法和分析法
第1课时 综 合 法综合法 已知条件定义公理定理推理论证已知条件定义公理定理所要证明的结论1.判一判(正确的打“√”,错误的打“×”)
(1)综合法是执果索因的逆推证法.( )
(2)综合法证明的依据是三段论.( )
(3)综合法的推理过程实际上是寻找它的必要条件.( )【解析】(1)错误.综合法是一种由因导果的顺推证法.
(2)正确.综合法的逻辑依据是三段论.
(3)正确.综合法从“已知”看“可知”,逐步推出“未知”,其逐步推理实际上是寻找它的必要条件.
答案:(1)× (2)√ (3)√2.做一做(请把正确的答案写在横线上)
(1)已知函数f(x)=ax2+bx+c是偶函数,则b的值为 .
(2)在不等式“a2+b2≥2ab”的证明中:因为a2+b2-2ab=(a-b)2≥0所以a2+b2≥2ab,该证明用的方法是 .
(3)角A,B为△ABC内角,A>B是sinA>sinB的 条件(填“充分”“必要”“充要”或“既不充分又不必要”).【解析】(1)由于f(x)为偶函数.所以f(-x)=f(x).
所以ax2-bx+c=ax2+bx+c,
所以-bx=bx,所以b=0.
答案:0
(2)由因导果,易知该证法为综合法.
答案:综合法
(3)角A,B为△ABC内角且A>B,所以sinA>sinB,由sinA>sinB(A,B均为△ABC的内角)知A>B.
答案:充要【要点探究】
知识点 综合法
1.综合法的基本思路
综合法的基本思路是“由因导果”,由已知走向求证,即从数学题的已知条件出发,经过逐步的逻辑推理,最后导出待证结论或需求的问题.2.综合法的两个特点
(1)用综合法证明不等式,证明步骤严谨,逐层递进,步步为营,条理清晰,形式简洁,宜于表达推理的思维轨迹.
(2)因用综合法证明命题“若A则D”的思考过程可表示为:故要从A推理到D,由A推演出的中间结论未必唯一,如B,B1,B2等,可由B,B1,B2进一步推演出的中间结论则可能更多,如C,C1,C2,C3,C4等等.
所以如何找到“切入点”和有效的推理途径是有效利用综合法证明问题的“瓶颈”. 【知识拓展】综合法证明不等式时常用的不等式
(1)a2+b2≥2ab(当且仅当a=b时取等号).
(2) (a,b∈R*,当且仅当a=b时取等号).
(3)a2≥0,|a|≥0,(a-b)2≥0.
(4) ≥2(a,b同号). ≤-2(a,b异号).
(5)a,b∈R,a2+b2≥ (a+b)2.(6)不等式的性质
定理1 对称性:a>b?b
定理3 加法性质: ?a+c>b+c.
推论 ?a+c>b+d.
定理4 乘法性质: ?ac>bc.
推论1 ?ac>bd.
推论2 ?an>bn.
定理5 开方性质:【微思考】
综合法的推理过程是合情推理还是演绎推理?
提示:综合法的推理过程是演绎推理,它的每一步推理都是严密的逻辑推理,得到的结论是正确的.【即时练】
1.下面的四个不等式:①a2+b2+3≥
ab+ (a+b);②a(1-a)≤ ;③ ≥2;④(a2+b2)·
(c2+d2)≥(ac+bd)2,其中恒成立的有 .
2.求证:a2+b2+c2≥ab+ac+bc.【解析】1.因为a2+b2≥2ab,a2+3≥2 a,b2+3≥2 b.相加
得2(a2+b2+3)≥2ab+2 (a+b),所以a2+b2+3≥ab+ (a+b),
所以①正确.由于a(1-a)- =-a2+a- =- ≤0.所以
②正确.(a2+b2)·(c2+d2)=a2c2+a2d2+b2c2+b2d2≥a2c2+2abcd+
b2d2=(ac+bd)2,所以④正确.而 ≥2,因为a,b的符号不确定,所以不一定成立.
答案:①②④2.因为a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc.
将此三式相加可得
2(a2+b2+c2)≥2ab+2ac+2bc,所以a2+b2+c2≥ab+ac+bc,
所以原式成立. 【题型示范】
类型一 用综合法证明三角问题
【典例1】
(1)在△ABC中,已知cosAcosB>sinAsinB,则△ABC的形状一定是 .
(2)在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=
(2b-c)sinB+(2c-b)sinC.
①求证:A的大小为60°;
②若sinB+sinC= .证明△ABC为等边三角形.【解题探究】1.题(1)中△ABC的形状可从哪些角度判断?
2.题(2)中①A的大小怎样与已知条件联系起来?②中怎样说明△ABC为等边三角形?
【探究提示】1.可以从边的角度或角的角度判断△ABC的形状,结合已知条件应从角的角度判断.
2.①中可利用正弦定理将角与边互化然后利用余弦定理求A;
②中由sinB+sinC= 及隐含条件A=60°可求B,C,说明△ABC的形状.【自主解答】(1)因为cosAcosB>sinAsinB,
所以cosAcosB-sinAsinB
=cos(A+B)>0.
因为0
即△ABC为钝角三角形.
答案:钝角三角形(2)①由2asinA=(2b-c)sinB+(2c-b)sinC,
得2a2=(2b-c)·b+(2c-b)c,
即bc=b2+c2-a2,
所以cosA=
所以A=60°.②由A+B+C=180°得B+C=120°,
由sin B+sin C= 得sin B+sin(120°-B)=
sin B+(sin 120°cos B-cos 120°sin B)=
sin B+ cos B=
即sin(B+30°)=1.
因为0°<B<120°,
所以30°<B+30°<150°,
所以B+30°=90°,即B=60°,
所以A=B=C=60°.
即△ABC为等边三角形.【方法技巧】
1.综合法处理问题的三个步骤2.证明三角等式的主要依据
(1)三角函数的定义、诱导公式及同角基本关系式.
(2)和、差、倍角的三角函数公式.
(3)三角形中的三角函数及三角形内角和定理.
(4)正弦定理、余弦定理和三角形的面积公式.【变式训练】已知a,b,c为△ABC的三边,x∈R,求证:方程a2x2+(b2-a2-c2)x+c2=0没有实数根.【证明】已知a,b,c为△ABC的三边,x∈R,和方程a2x2+(b2-a2-c2)x+c2=0.
根据根的判别式可知:Δ=(b2-a2-c2)2-4a2c2
=(b2-a2-c2+2ac)(b2-a2-c2-2ac)
=(b-a+c)(b+a-c)(b-a-c)(b+a+c),
又因为a,b,c是△ABC的三边,
故b-a+c>0,b+a-c>0,b-a-c<0,b+a+c>0.
所以Δ=(b-a+c)(b+a-c)(b-a-c)(b+a+c)<0,
故方程a2x2+(b2-a2-c2)x+c2=0没有实数根.【补偿训练】求证:sin3α=3sinα-4sin3α.
【解析】左边=sin(2α+α)
=sin2αcosα+cos2αsinα
=2sinαcos2α+(1-2sin2α)sinα
=2sinα(1-sin2α)+sinα-2sin3α
=2sinα-2sin3α+sinα-2sin3α
=3sinα-4sin3α=右边.
所以sin3α=3sinα-4sin3α.类型二 综合法在数列中的应用
【典例2】
(1)已知方程(x2-mx+2)(x2-nx+2)=0的四个根组成一个首项为 的等比数列,则|m-n|= .(2)设数列{an}的前n项和为Sn,满足(3-m)Sn+2man=m+3(n∈N*).其中m为常数,且m≠-3,m≠0.
①求证:{an}是等比数列.
②若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=
f(bn-1)(n∈N*,n≥2),求证:{ }为等差数列.【解题探究】1.题(1)中m,n的值怎样求解?
2.题(2)①中证明等比数列的关键是什么?②中怎样说明为
{ }等差数列?
【探究提示】1.利用根与系数的关系结合等比数列的性质可求m,n.
2.①中关键是利用an+1与Sn和Sn+1之间的关系结合等比数列的
定义;②中利用定义说明,即 常数(n≥2).【自主解答】(1)方程(x2-mx+2)(x2-nx+2)=0?x2-mx+2=0①
或x2-nx+2=0②.设方程①两根为x1,x4,方程②两根为x2,x3.
则x1·x4=2,x1+x4=m,x2·x3=2,x2+x3=n.因为方程(x2-mx+2)
(x2-nx+2)=0的四个根组成一个首项为 的等比数列.所以
x1,x2,x3,x4分别为此数列的前四项且x1= ,x4= =4,公比
为2,所以x2=1,x3=2,所以m=x1+x4= +4= ,n=x2+x3=1+2=3,
故|m-n|=
答案:(2)①由(3-m)Sn+2man=m+3,得(3-m)Sn+1+2man+1=m+3,两式相减得(3+m)an+1=2man,
因为m≠0且m≠-3,
所以
所以{an}是等比数列.
②因为b1=a1=1,q=f(m)=
所以n∈N*且n≥2时,
所以{ }是以1为首项, 为公差的等差数列.【延伸探究】题(2)①中若m=1试求{an}的前n项和.
【解析】若m=1则
由已知得(3-1)S1+2a1=4,
所以a1=1,
即数列{an}是以1为首项为 公比的等比数列.
=2-21-n.【方法技巧】综合法证明数列问题的依据【变式训练】在数列{an}中,a1=1,an+1=2an+2n.
(1)设bn= ,求证数列{bn}是等差数列.
(2)求数列{an}的前n项和Sn.
【解题指南】用综合法证明有关数列的问题,同时要注意理解等差数列的含义.【解析】(1)因为an+1=2an+2n,
所以
因为bn=
所以bn+1= =bn+1,
所以数列{bn}是等差数列,其中b1=1,公差为1,
所以bn=n,an=n·2n-1.(2)因为Sn=1×20+2×21+…+(n-1)·2n-2+n·2n-1,
所以2Sn=1×21+2×22+…+(n-1)·2n-1+n·2n,
两式相减得Sn=n·2n-1×20-1×21-…-1×2n-1
=n·2n-2n+1=2n(n-1)+1.【补偿训练】在等比数列{an}中,首项a1>1,公比q>0,n∈N,且n>1.求证lgan+1lgan-1<(lgan)2.【证明】因为{an}为等比数列,
所以 =an-1·an+1(n>1).
又因为a1>1,公比q>0,n∈N,且n>1,
所以lgan-1lgan+1<
所以lgan+1lgan-1<(lgan)2.【规范解答】综合法在几何证明中的应用
【典例】(12分)如图,在四棱锥O-ABCD中,
底面ABCD为菱形,OA⊥平面ABCD,E为OA的
中点,F为BC的中点,求证:
(1)平面BDO⊥平面ACO.
(2)EF∥平面OCD.【审题】抓信息,找思路【点题】警误区,促提升
失分点1:证明时忽略①处条件的运用导致无法证明面面垂直,考试时最多得2分.
失分点2:证明时不能正确地构造出平行四边形,从而无法得到线线平行如本题中②则会导致第(2)问无法证出,实际考试中最多得8分.【悟题】提措施,导方向
1.关注题中的条件
证明时要注意应用题中的条件,注意隐含条件的挖掘,如果漏掉某一条件或对某一条件挖掘不深则会导致题目无法证明,如本例中ABCD为菱形的条件.
2.注重定理的应用
几何证明的前提是熟练地应用各个判定定理及性质定理,注意各个定理的应用格式,掌握常见的辅助线的作法,寻找好定理所需的条件,如本例中构造平行四边形说明线线平行.【类题试解】如图,正方形ABCD和四边形ACEF所在的平面互
相垂直,CE⊥AC,EF∥AC,AB= ,CE=EF=1.
(1)求证:AF∥平面BDE.
(2)求证:CF⊥平面BDE.【证明】(1)设AC与BD的交点是G.因为EF∥AG,且EF=1,
AG= AC=1,
所以四边形AGEF为平行四边形,所以AF∥EG,因为EG?平面BDE,AF?平面BDE,
所以AF∥平面BDE.(2)连接FG,因为EF∥CG,EF=CG=1,所以四边形CEFG为平行四边形,
又因为CE=EF=1,所以四边形CEFG为菱形,所以EG⊥CF.
在正方形ABCD中,AC⊥BD.
因为正方形ABCD和四边形ACEF所在的平面互相垂直,
所以BD⊥平面CEFG,
所以BD⊥CF,又因为EG∩BD=G,所以CF⊥平面BDE.
