河北省平泉县第四中学人教版七年级下册数学课件:6.1.2 平方根(共16张ppt)
文档属性
| 名称 | 河北省平泉县第四中学人教版七年级下册数学课件:6.1.2 平方根(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 413.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-13 22:12:54 | ||
图片预览






文档简介
课件16张PPT。6.1.2平方根 一般地,如果一个正数x 的平方等于a,
即 ,那么这个正数x 叫做a的算术平方根。 算术平方根规定:0 的算术平方根是 0a的算术平方根记为读作“根号a”,a 叫做 被开方数。复习1、 求下列各数的算术平方根:
(1) 0.0025; (2) 121; (3) 32 2、 求下列各式的值:
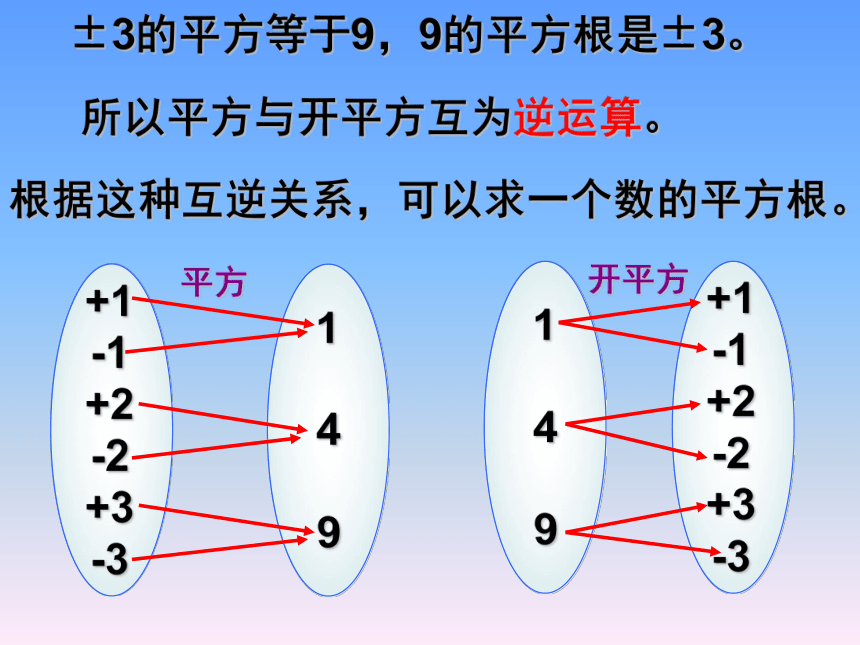
(1) (2) (3) (4)=1=2练一练 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根)。即:如果x2=a,则x叫做a的平方根。如果一个数的平方等于9,那么这个数是多少?探究 例如,3和- 3是9的平方根,
简记为±3是9的平方根。求一个数a的平方根的运算,叫做开平方。3或-3。32 = 9 ,且 (-3)2 = 9, ±3的平方等于9,9的平方根是±3。
所以平方与开平方互为逆运算。
根据这种互逆关系,可以求一个数的平方根。平方开平方(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的平方根为±10,即 = ± 10。(2)因为 = ,所以 的平方根是 ,(3)因为 =0.0001, 所以0.0001的平方根为±0.01,即 =±0.01。例题求下列各数的平方根:即 = ; 求一个非负数 a 的平方根,就是把平方后等于 a 的数找出来,从而求出 a 的平方根。当 a 是一个正数时,不要漏掉负的平方根。 正数的平方根有什么特点?
0的平方根是多少?负数有平方根吗?归纳正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根;1、平方根的性质:2、平方根的记法:(1) 表示非负数 a 的正的平方根,
- 表示非负数 a 的负的平方根;
(2)± 表示非负数 a 的平方根,
与- 互为相反数;
(3) 在± 中,a≥0。 非负数a的平方根用符号“± ” 表示,读作:“正、负根号a”。1、下列各数有平方根吗?说明理由。(1)-4;(2)(-4)2;(3)-42; (4)0; (5)(-2)3;(6)3 判断一个数有无平方根,要注意这个数的符号。当这个数为正数时,它有两个平方根;
当这个数为0时,它有一个平方根0;
当这个数为负数时,它没有平方根。练习√××√×√3、 下列说法正确的是:( )(A)5是25的一个平方根;(B)25的平方根是 5;(C)-1的平方根是 -1;(D)(-1)2的平方根是 -1。±0.6±100A(3)- = - 13解:(1)± =±7 4、求下列各式的值。(2) = 巩固练习: 1、已知一个数的平方根是它本身,
则这个数是 。3、108的平方根是 ; 的平方根是 ; 4、判断:一个非负数的平方根一定是
非负数. ( )0× 5、( )。 6、若 成立, 则 =__
若一个数的算术平方根小于它本身,
这个数的取值范围是 ( )。 8、已知 m 的平方根是 2a-3 和 a-12, 求 a和m 的值。 7、若 25x2-36 = 0, 则 x = ;
若 (2x)2 = 0.36, 则 x = ; 9、若 求ab的值。168大于1作业:
47页----习题6.1练习:
46页练习题再见
即 ,那么这个正数x 叫做a的算术平方根。 算术平方根规定:0 的算术平方根是 0a的算术平方根记为读作“根号a”,a 叫做 被开方数。复习1、 求下列各数的算术平方根:
(1) 0.0025; (2) 121; (3) 32 2、 求下列各式的值:
(1) (2) (3) (4)=1=2练一练 一般地,如果一个数的平方等于a,那么这个数叫做a的平方根(也叫二次方根)。即:如果x2=a,则x叫做a的平方根。如果一个数的平方等于9,那么这个数是多少?探究 例如,3和- 3是9的平方根,
简记为±3是9的平方根。求一个数a的平方根的运算,叫做开平方。3或-3。32 = 9 ,且 (-3)2 = 9, ±3的平方等于9,9的平方根是±3。
所以平方与开平方互为逆运算。
根据这种互逆关系,可以求一个数的平方根。平方开平方(1)100 (2) (3)0.0001解:(1)因为 =100,所以100的平方根为±10,即 = ± 10。(2)因为 = ,所以 的平方根是 ,(3)因为 =0.0001, 所以0.0001的平方根为±0.01,即 =±0.01。例题求下列各数的平方根:即 = ; 求一个非负数 a 的平方根,就是把平方后等于 a 的数找出来,从而求出 a 的平方根。当 a 是一个正数时,不要漏掉负的平方根。 正数的平方根有什么特点?
0的平方根是多少?负数有平方根吗?归纳正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根;1、平方根的性质:2、平方根的记法:(1) 表示非负数 a 的正的平方根,
- 表示非负数 a 的负的平方根;
(2)± 表示非负数 a 的平方根,
与- 互为相反数;
(3) 在± 中,a≥0。 非负数a的平方根用符号“± ” 表示,读作:“正、负根号a”。1、下列各数有平方根吗?说明理由。(1)-4;(2)(-4)2;(3)-42; (4)0; (5)(-2)3;(6)3 判断一个数有无平方根,要注意这个数的符号。当这个数为正数时,它有两个平方根;
当这个数为0时,它有一个平方根0;
当这个数为负数时,它没有平方根。练习√××√×√3、 下列说法正确的是:( )(A)5是25的一个平方根;(B)25的平方根是 5;(C)-1的平方根是 -1;(D)(-1)2的平方根是 -1。±0.6±100A(3)- = - 13解:(1)± =±7 4、求下列各式的值。(2) = 巩固练习: 1、已知一个数的平方根是它本身,
则这个数是 。3、108的平方根是 ; 的平方根是 ; 4、判断:一个非负数的平方根一定是
非负数. ( )0× 5、( )。 6、若 成立, 则 =__
若一个数的算术平方根小于它本身,
这个数的取值范围是 ( )。 8、已知 m 的平方根是 2a-3 和 a-12, 求 a和m 的值。 7、若 25x2-36 = 0, 则 x = ;
若 (2x)2 = 0.36, 则 x = ; 9、若 求ab的值。168大于1作业:
47页----习题6.1练习:
46页练习题再见
