14.2两边及其夹角分别相等的两个三角形全等 同步练习(含答案)
文档属性
| 名称 | 14.2两边及其夹角分别相等的两个三角形全等 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 217.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-13 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.两边及其夹角分别相等的两个三角形
一、选择题
1.
如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件(
)
A.∠1=∠2
B.∠B=∠C
C.∠D=∠E
D.∠BAE=∠CAD
2.
能判定△ABC≌△A′B′C′的条件是(
)
A.AB=A′B′,AC=A′C′,∠C=∠C′
B.
AB=A′B′,
∠A=∠A′,BC=B′C′
C.
AC=A′C′,
∠A=∠A′,BC=B′C
D.
AC=A′C′,
∠C=∠C′,BC=B′C
3.
如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是(
)
A.
AB∥CD
B.
AD∥BC
C.
∠A=∠C
D.
∠ABC=∠CDA
4.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )21教育网
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.AC=DC,∠A=∠D
5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )21cnjy.com
A.1对
B.2对
C.3对
D.4对
6.在△ABC和中,∠C=,b-a=,b+a=,则这两个三角形(
)
A.
不一定全等
B.不全等
C.
全等,根据“ASA”
D.
全等,根据“SAS”
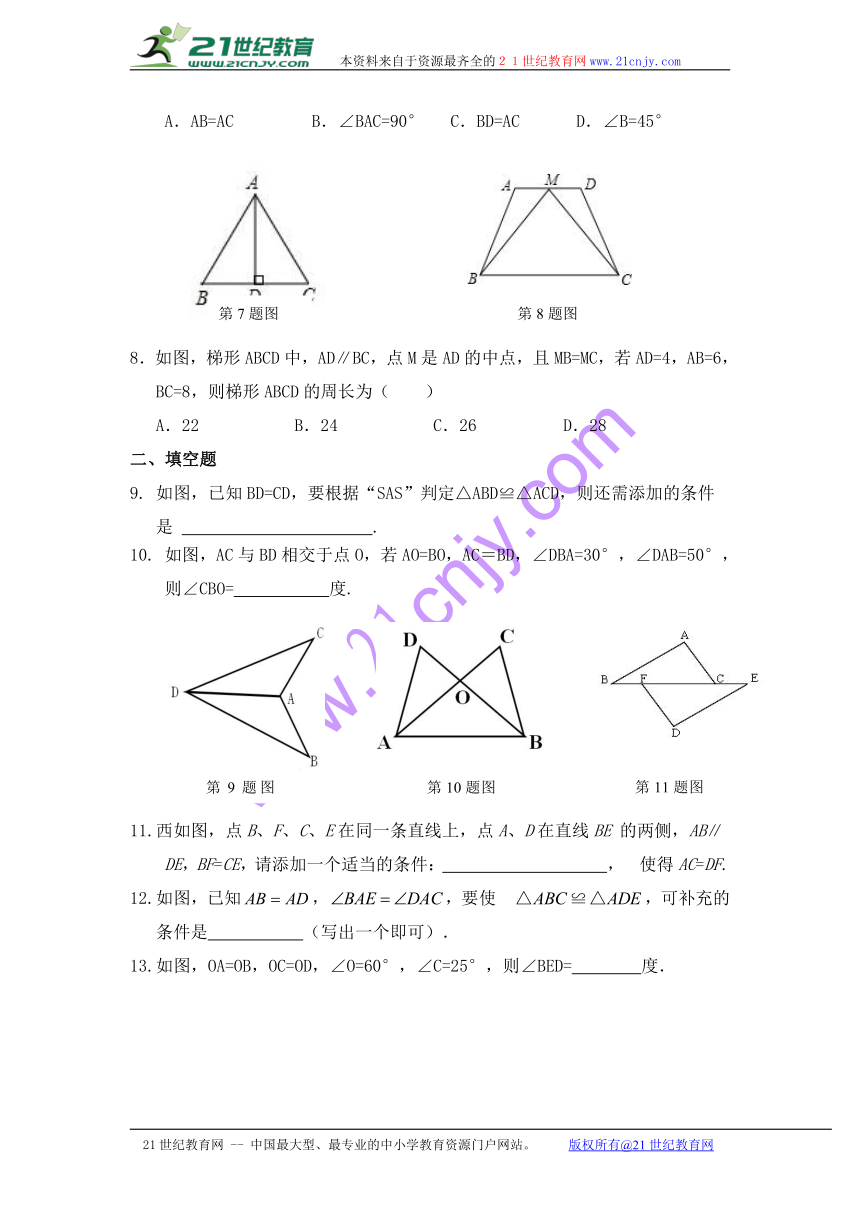
7.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
8.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为( )www.21-cn-jy.com
A.22
B.24
C.26
D.28
二、填空题
9.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.2·1·c·n·j·y
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.西如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,
使得AC=DF.
12.如图,已知,,要使
≌,可补充的条件是
(写出一个即可).
13.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED=
度.
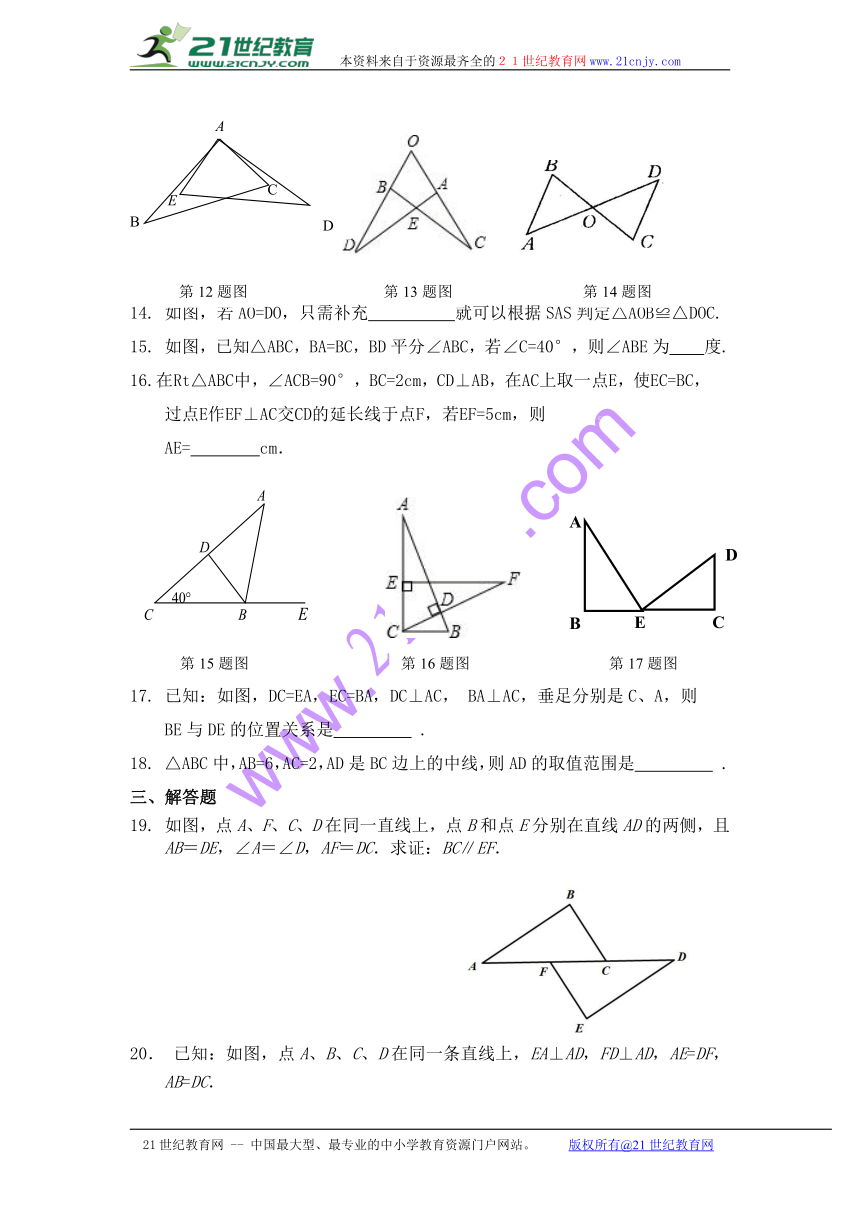
14.
如图,若AO=DO,只需补充
就可以根据SAS判定△AOB≌△DOC.
15.
如图,已知△ABC,BA=BC,BD平分∠ABC,若∠C=40°,则∠ABE为
度.
16.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则21·cn·jy·com
AE=
cm.
17.
已知:如图,DC=EA,EC=BA,DC⊥AC,
BA⊥AC,垂足分别是C、A,则
BE与DE的位置关系是
.
18.
△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是
.
三、解答题
19.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.
21世纪教育网版权所有
20.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.【来源:21·世纪·教育·网】
求证:∠ACE=∠DBF.
21.
如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.
22.
如图,AB=AC,点E、F分别是AB、AC的中点,求证:△AFB≌△AEC.
23.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。21·世纪
教育网
第2课时
边角边(SAS)
一、选择题
1.
A
2.
D
3.
B
4.
C
5.
C
6.
D
7.
A
8.
Bwww-2-1-cnjy-com
二、填空题
9.
∠CDA=∠BDA
10.
20
11.
AB=DE.
12.
AE=AC(答案不唯一);
13.
70
14.
BO=CO
15.
80
16.
6
17.
垂直
18.
2
<
AD
<
4
三、解答题
19.
证明:∵AF=DC,∴AC=DF,
又∵∠A=∠D
,
∴AB=DE,∴△ABC≌△DEF,
∴∠ACB=∠DFE,∴BC∥EF.
20.
证明:∵AB=DC
∴AC=DB
∵EA⊥AD,FD⊥AD
∴∠A=∠D=90°
在△EAC与△FDB中
∴△EAC≌△FDB
∴∠ACE=∠DBF.
21.
证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠BCE+∠ACE,
∴∠DCE=∠ACB,
∵在△DCE和△ACB中
,
∴△DCE≌△ACB,∴DE=AB.
22.
证明:∵点E、F分别是AB、AC的中点,
∴AE=AB,AF=AC,
∵AB=AC,∴AE=AF,
在△AFB和△AEC中,
AB=AC,∠A=∠A,AE=AF,
∴△AFB≌△AEC.
23.
解:AE=EF.
理由如下:
∵四边形ABCD是正方形,∴AB=BC
又∵BH=BE
∴AH=CE
∵△BHE为等腰直角三角形.∴∠H=45°
∵CF平分∠DCE
∴∠FCE=∠H=45°
∵AE⊥EF,
∠ABE=90°
∴∠BAE+∠BEH=∠BEH+∠FEM=90°
即:∠BAE=∠FEM
∴∠HAE=∠CEF
在△HAE和△CEF中,
∠H=∠FCE,AH=CE,∠HAE=∠CEF
∴△HAE≌△CEF,
∴AE=EF.
第1题
第5题图
第4题图
第3题图
第7题图
第8题图
第9题图图
第11题图图
第10题图图
D
A
C
E
B0
第12题图图
第13题图图
第14题图图
C
E
D
B
A
第15题图图
第17题图图
第16题图图
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
1.两边及其夹角分别相等的两个三角形
一、选择题
1.
如图,AB=AC,AD=AE,欲证△ABD≌△ACE,可补充条件(
)
A.∠1=∠2
B.∠B=∠C
C.∠D=∠E
D.∠BAE=∠CAD
2.
能判定△ABC≌△A′B′C′的条件是(
)
A.AB=A′B′,AC=A′C′,∠C=∠C′
B.
AB=A′B′,
∠A=∠A′,BC=B′C′
C.
AC=A′C′,
∠A=∠A′,BC=B′C
D.
AC=A′C′,
∠C=∠C′,BC=B′C
3.
如图,AD=BC,要得到△ABD和△CDB全等,可以添加的条件是(
)
A.
AB∥CD
B.
AD∥BC
C.
∠A=∠C
D.
∠ABC=∠CDA
4.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )21教育网
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.AC=DC,∠A=∠D
5.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )21cnjy.com
A.1对
B.2对
C.3对
D.4对
6.在△ABC和中,∠C=,b-a=,b+a=,则这两个三角形(
)
A.
不一定全等
B.不全等
C.
全等,根据“ASA”
D.
全等,根据“SAS”
7.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
8.如图,梯形ABCD中,AD∥BC,点M是AD的中点,且MB=MC,若AD=4,AB=6,BC=8,则梯形ABCD的周长为( )www.21-cn-jy.com
A.22
B.24
C.26
D.28
二、填空题
9.
如图,已知BD=CD,要根据“SAS”判定△ABD≌△ACD,则还需添加的条件是
.2·1·c·n·j·y
10.
如图,AC与BD相交于点O,若AO=BO,AC=BD,∠DBA=30°,∠DAB=50°,
则∠CBO=
度.
11.西如图,点B、F、C、E在同一条直线上,点A、D在直线BE
的两侧,AB∥DE,BF=CE,请添加一个适当的条件:
,
使得AC=DF.
12.如图,已知,,要使
≌,可补充的条件是
(写出一个即可).
13.如图,OA=OB,OC=OD,∠O=60°,∠C=25°,则∠BED=
度.
14.
如图,若AO=DO,只需补充
就可以根据SAS判定△AOB≌△DOC.
15.
如图,已知△ABC,BA=BC,BD平分∠ABC,若∠C=40°,则∠ABE为
度.
16.在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=5cm,则21·cn·jy·com
AE=
cm.
17.
已知:如图,DC=EA,EC=BA,DC⊥AC,
BA⊥AC,垂足分别是C、A,则
BE与DE的位置关系是
.
18.
△ABC中,AB=6,AC=2,AD是BC边上的中线,则AD的取值范围是
.
三、解答题
19.
如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:BC∥EF.
21世纪教育网版权所有
20.
已知:如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.【来源:21·世纪·教育·网】
求证:∠ACE=∠DBF.
21.
如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.
22.
如图,AB=AC,点E、F分别是AB、AC的中点,求证:△AFB≌△AEC.
23.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由。21·世纪
教育网
第2课时
边角边(SAS)
一、选择题
1.
A
2.
D
3.
B
4.
C
5.
C
6.
D
7.
A
8.
Bwww-2-1-cnjy-com
二、填空题
9.
∠CDA=∠BDA
10.
20
11.
AB=DE.
12.
AE=AC(答案不唯一);
13.
70
14.
BO=CO
15.
80
16.
6
17.
垂直
18.
2
<
AD
<
4
三、解答题
19.
证明:∵AF=DC,∴AC=DF,
又∵∠A=∠D
,
∴AB=DE,∴△ABC≌△DEF,
∴∠ACB=∠DFE,∴BC∥EF.
20.
证明:∵AB=DC
∴AC=DB
∵EA⊥AD,FD⊥AD
∴∠A=∠D=90°
在△EAC与△FDB中
∴△EAC≌△FDB
∴∠ACE=∠DBF.
21.
证明:∵∠DCA=∠ECB,
∴∠DCA+∠ACE=∠BCE+∠ACE,
∴∠DCE=∠ACB,
∵在△DCE和△ACB中
,
∴△DCE≌△ACB,∴DE=AB.
22.
证明:∵点E、F分别是AB、AC的中点,
∴AE=AB,AF=AC,
∵AB=AC,∴AE=AF,
在△AFB和△AEC中,
AB=AC,∠A=∠A,AE=AF,
∴△AFB≌△AEC.
23.
解:AE=EF.
理由如下:
∵四边形ABCD是正方形,∴AB=BC
又∵BH=BE
∴AH=CE
∵△BHE为等腰直角三角形.∴∠H=45°
∵CF平分∠DCE
∴∠FCE=∠H=45°
∵AE⊥EF,
∠ABE=90°
∴∠BAE+∠BEH=∠BEH+∠FEM=90°
即:∠BAE=∠FEM
∴∠HAE=∠CEF
在△HAE和△CEF中,
∠H=∠FCE,AH=CE,∠HAE=∠CEF
∴△HAE≌△CEF,
∴AE=EF.
第1题
第5题图
第4题图
第3题图
第7题图
第8题图
第9题图图
第11题图图
第10题图图
D
A
C
E
B0
第12题图图
第13题图图
第14题图图
C
E
D
B
A
第15题图图
第17题图图
第16题图图
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
