14.2.2两角及其夹边分别相等的两个三角形(教案)
文档属性
| 名称 | 14.2.2两角及其夹边分别相等的两个三角形(教案) |
|
|
| 格式 | zip | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 14:09:57 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2.两角及其夹边分别相等的两个三角形
教学目标
1.知识与技能
理解“角边角”判定两个三角形全等的方法。
2过程与方法
经历探究“角边角”判定两个三角形全等的过程,能进行有条理的思索。
3情感态度与价值观
培养严谨的表述能力,体会几何中逻辑推理的应用价值
教学重点
学会运用“角边角”判定两个三角形全等的方法
教学难点
如何进行推理分析
教学过程
复习回顾
回忆“边角边”定理
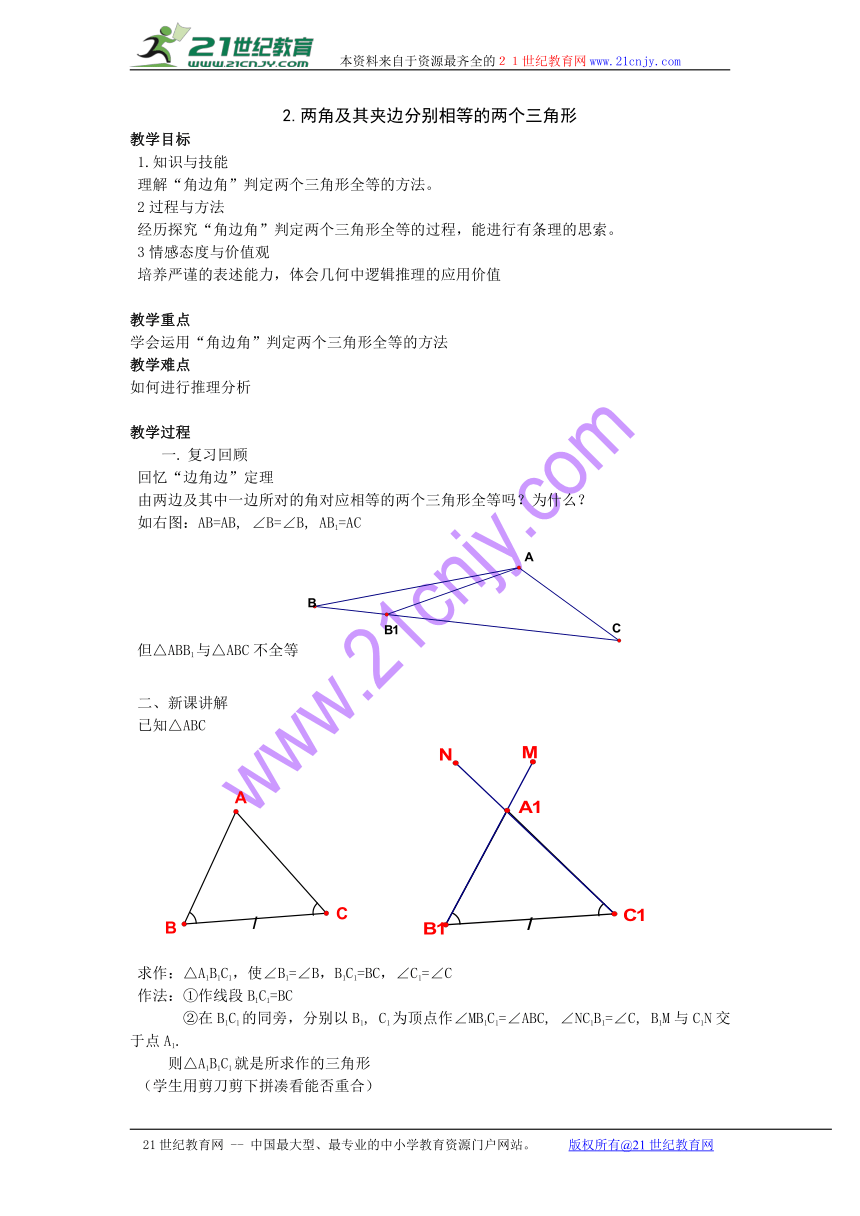
由两边及其中一边所对的角对应相等的两个三角形全等吗?为什么?
如右图:AB=AB,
∠B=∠B,
AB1=AC
但△ABB1与△ABC不全等
二、新课讲解
已知△ABC
求作:△A1B1C1,使∠B1=∠B,B1C1=BC,∠C1=∠C
作法:①作线段B1C1=BC
②在B1C1的同旁,分别以B1,
C1为顶点作∠MB1C1=∠ABC,
∠NC1B1=∠C,
B1M与C1N交于点A1.21世纪教育网版权所有
则△A1B1C1就是所求作的三角形
(学生用剪刀剪下拼凑看能否重合)
全等三角形判定定理2:
两角和它们的夹边对应相等的两个三角形全等,记为“角边角”或“ASA”
三、例题分析
1.
例1.已知:如下图所示,∠1=∠2,
∠3=∠4,
求证:△ADC≌△BCD
证明:∵∠1=∠2,
∠3=∠4
(已知)
∴∠1+∠3=∠2+∠4
即∠ADC=∠BCD
在△ADC和△BCD中
∴△ADC≌△BCD
(ASA)
归纳:在证明三角形全等时要善于把间接的条件转化为可以直接判定三角形全等的条件
2.阅读课本P101例3、例4
在阅读中总结出证明方法,形成证明模式。
四、课堂练习
P102练习
1,2,3
五.小结
角边角定理:两角和它们的夹边对应相等的两个三角形全等
六.作业布置
P111习题14.2第2、4题
七.反思:
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
2.两角及其夹边分别相等的两个三角形
教学目标
1.知识与技能
理解“角边角”判定两个三角形全等的方法。
2过程与方法
经历探究“角边角”判定两个三角形全等的过程,能进行有条理的思索。
3情感态度与价值观
培养严谨的表述能力,体会几何中逻辑推理的应用价值
教学重点
学会运用“角边角”判定两个三角形全等的方法
教学难点
如何进行推理分析
教学过程
复习回顾
回忆“边角边”定理
由两边及其中一边所对的角对应相等的两个三角形全等吗?为什么?
如右图:AB=AB,
∠B=∠B,
AB1=AC
但△ABB1与△ABC不全等
二、新课讲解
已知△ABC
求作:△A1B1C1,使∠B1=∠B,B1C1=BC,∠C1=∠C
作法:①作线段B1C1=BC
②在B1C1的同旁,分别以B1,
C1为顶点作∠MB1C1=∠ABC,
∠NC1B1=∠C,
B1M与C1N交于点A1.21世纪教育网版权所有
则△A1B1C1就是所求作的三角形
(学生用剪刀剪下拼凑看能否重合)
全等三角形判定定理2:
两角和它们的夹边对应相等的两个三角形全等,记为“角边角”或“ASA”
三、例题分析
1.
例1.已知:如下图所示,∠1=∠2,
∠3=∠4,
求证:△ADC≌△BCD
证明:∵∠1=∠2,
∠3=∠4
(已知)
∴∠1+∠3=∠2+∠4
即∠ADC=∠BCD
在△ADC和△BCD中
∴△ADC≌△BCD
(ASA)
归纳:在证明三角形全等时要善于把间接的条件转化为可以直接判定三角形全等的条件
2.阅读课本P101例3、例4
在阅读中总结出证明方法,形成证明模式。
四、课堂练习
P102练习
1,2,3
五.小结
角边角定理:两角和它们的夹边对应相等的两个三角形全等
六.作业布置
P111习题14.2第2、4题
七.反思:
21世纪教育网
--
中国最大型、最专业的中小学教育资源门户网站。
版权所有@21世纪教育网
