1.1.2 四种命题 课件2
图片预览










文档简介
课件37张PPT。1.1.2
四 种 命 题1.原命题与逆命题条件结论“若q,则p”2.原命题与否命题否定“若﹁p,则﹁q”3.原命题与逆否命题“若﹁q,则﹁p”否定互换1.判一判(正确的打“√”,错误的打“×”)
(1)有的命题没有逆命题.( )
(2)“对顶角相等”的否命题为“对顶角不相等”.( )
(3)原命题的否命题的逆命题就是原命题的逆否命题.( )【解析】(1)错误.任何命题都是由条件和结论构成的,所以任何命题都有逆命题.
(2)错误.“对顶角相等”的否命题为“不是对顶角的两个角不相等”.
(3)正确.原命题“若p,则q”的否命题为“若﹁p,则﹁q”,这个命题的逆命题为“若﹁q,则﹁p”,这就是原命题的逆否命题.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)若a=0,则ab=0的逆命题是 .
(2)若命题r的否命题为“若﹁p,则q”,那么原命题r为________.
(3)若a=b,则|a|=|b|的逆否命题是 .【解析】(1)逆命题只需把原命题的条件与结论互换即可,即逆命题为若ab=0,则a=0.
答案:若ab=0,则a=0
(2)因为原命题与否命题为互否命题,所以只需求“若﹁p,则q”的否命题即可,其否命题为“若p,则﹁q”.
答案:“若p,则﹁q”
(3)逆否命题既需要把原命题的条件与结论否定,又需要互换,故已知命题的逆否命题是:若|a|≠|b|,则a≠b.
答案:若|a|≠|b|,则a≠b【要点探究】
知识点 四种命题
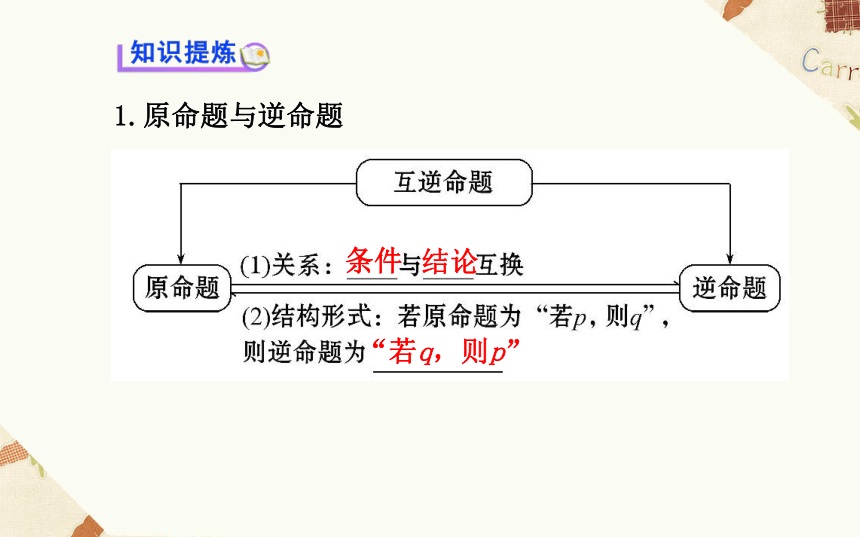
1.原命题与逆命题
(1)逆命题是将原命题的条件与结论互换,写原命题的逆命题时,不要交换命题的前提条件.
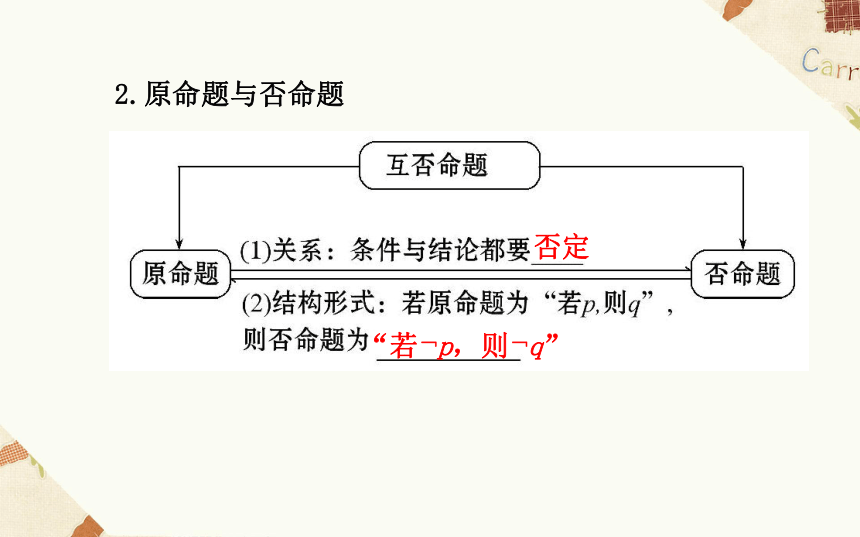
(2)原命题的逆命题与原命题是互逆的,即逆命题的逆命题是原命题.2.原命题与否命题
(1)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.
(2)原命题也可以看作是它的否命题的否命题,即原命题与否命题是互为否命题的.
3.原命题与逆否命题
将原命题的条件和结论“换位”得逆命题,“换质”(即否定)得否命题,既“换位”又“换质”得逆否命题.【知识拓展】常见词语的否定【微思考】
(1)任何一个命题都有逆命题、否命题和逆否命题吗?
提示:因为任何一个命题都包含条件和结论两部分,通过条件和结论的不同变换都可以得到这个命题的逆命题、否命题和逆否命题.因此任何一个命题都有逆命题、否命题和逆否命题.
(2)解决四种命题转换的关键是什么?
提示:明确原命题的逆命题、否命题、逆否命题的条件和结论的位置关系和否定关系是解决四种命题的关键.【即时练】
命题p:若a=1则a2=1;命题q:若a2=1则a=1,则命题p与q的关系是 .
【解析】因为命题p与q的条件与结论正好相反,故p与q是互逆命题.
答案:互逆命题【题型示范】
类型一 写原命题的其他三种命题
【典例1】
(1)命题“两对角线相等的四边形是矩形”是命题“矩形是两条对角线相等的四边形”的( )
A.逆命题 B.否命题
C.逆否命题 D.等价命题(2)写出命题“若抛物线y=ax2+bx+c的开口向下,则集合{x|ax2+bx+c<0}≠?”的逆命题,否命题,逆否命题.【解题探究】1.题(1)中两命题的条件与结论是什么关系?
2.题(2)中命题的条件与结论各是什么?
【探究提示】1.两命题的条件与结论是互换的.
2.题(2)中命题的条件是:抛物线y=ax2+bx+c的开口向下;结论是集合{x|ax2+bx+c<0}≠?.【自主解答】(1)选A.将条件和结论互换,得到的是逆命题.故
选A.
(2)逆命题:若集合{x|ax2+bx+c<0}≠?,则抛物线y=ax2+bx+c的
开口向下.
否命题:若抛物线y=ax2+bx+c的开口向上,则集合{x|ax2+bx+c<
0}=?.
逆否命题:若集合{x|ax2+bx+c<0}=?,则抛物线y=ax2+bx+c的开
口向上.【方法技巧】四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.【变式训练】设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是( )
A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b|
C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b
【解析】选D.命题“若a=-b,则|a|=|b|”的逆命题是“若|a|=|b|,则a=-b”.故选D.【补偿训练】命题“若a>b,则a-8>b-8”的逆否命题是( )
A.若ab-8,则a>b
C.若a≤b,则a-8≤b-8 D.若a-8≤b-8,则a≤b
【解析】选D.逆否命题是将原命题中的条件和结论既交换又否定,故应选D.类型二 四种命题及其真假判断
【典例2】
(1)命题“个位数字为5的整数能被5整除”是 (填“真”或“假”)命题,它的逆命题为 ,是 (填“真”或“假”)命题.
(2)把下列命题改写成“若p,则q”的形式,并分别写出它们的逆命题、否命题与逆否命题,并判断真假:
①负数小于零.②在三角形中,大边对大角.【解题探究】1.题(1)中能被5整除的整数个位数字有什么特点?命题的条件与结论各是什么?
2.题(2)中的命题写成“若p,则q”的形式如何写?
【探究提示】1.能被5整除的整数个位数字是0或5,命题的条件是“整数的个位数字为5”,结论是“整数能被5整除”.
2.①可写为:若一个数是负数,则它小于零,
②可写为:在三角形中,若边长a最大,则它所对的角A也最大.【自主解答】(1)命题“个位数字为5的整数能被5整除”是真命题,它的逆命题为:“能被5整除的整数的个位数字为5”,如20能被5整除,个位数字为0,是假命题.
答案:真 能被5整除的整数的个位数字为5 假
(2)①原命题:若一个数是负数,则它小于零.真命题.
逆命题:若一个数小于零,则它是负数.真命题.
否命题:若一个数不是负数,则它不小于零.真命题.
逆否命题:若一个数不小于零,则它不是负数.真命题.②原命题:在三角形中,大边对大角.真命题.
逆命题:在三角形中,大角对大边.真命题.
否命题:在三角形中,不是较大的边所对的角不是较大的.真命题.
逆否命题:在三角形中,不是较大的角所对的边不是较大的.真命题.【延伸探究】本题(1)命题的否命题为 ,
是 (填“真”或“假”)命题.
【解析】题(1)命题的否命题是:个位数字不是5的整数不能被5
整除,是假命题.
答案:个位数字不是5的整数不能被5整除 假【误区警示】本题中命题的否命题易误写为“个位数字是5的整数不能被5整除”的形式,导致出现这种错误的原因是忽略了否命题既要否定结论,还要否定条件.【方法技巧】判断四种命题真假的三种技巧
技巧一:根据学过的定义、公理、定理、性质直接判断命题的真假.
技巧二:根据已知的正确的结论,通过正确地推理所得到的命题是真命题.
技巧三:判断一个命题为假时,只要能找到一个反例就够了.【变式训练】写出命题“如果一个整数的各位数字之和能被3整除,则这个整数可以被3整除”的逆命题、否命题、逆否命题,并判断其真假.
【解析】逆命题:如果一个整数可以被3整除,则这个整数的各位数字之和能被3整除.(真命题)
否命题:如果一个整数的各位数字之和不能被3整除,则这个整数不能被3整除.(真命题)
逆否命题:如果一个整数不能被3整除,则这个整数的各位数字之和不能被3整除.(真命题)【补偿训练】设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,逆命题不成立的是
( )
A.当c⊥α时,若c⊥β,则α∥β
B.当b?α时,若b⊥β,则α⊥β
C.当b?α,且c是a在α内的射影时,若b⊥c,则a⊥b
D.当b?α,且c?α时,若c∥α,则b∥c【解析】选B.A.其逆命题是:当c⊥α时,若α∥β,则c⊥β,由面面平行的性质知正确.
B.其逆命题是:当b?α时,若α⊥β,则b⊥β,由相关知识知
b与β可能垂直,也可能平行,斜交.所以B不正确.
C.其逆命题是当b?α,且c是a在α内的射影时,若a⊥b,则b⊥c,由相关知识可知正确.
D.其逆命题是当b?α,且c?α时,若b∥c,则c∥α,由线面平行的判定定理知正确,故选B.【易错误区】对命题的条件和结论分不清致误
【典例】下列说法正确的是 .
(1)“若x2+y2=0,则x,y全为零”的否命题为“若x2+y2≠0,则x,y全不为零”.
(2)“正多边形都相似”的逆命题是真命题.
(3)“若x- 是有理数,则x是无理数”的逆否命题是真命题.【解析】(1)中否命题:“若x2+y2≠0则x,y不全为0”①,故是错
误的.
(2)中逆命题:“若两个多边形相似,则这两个多边形是正多边
形”②,是假命题,故此说法错误.
(3)中逆否命题:“若x不是无理数,则x- 不是有理数”,是真
命题.故说法正确.
答案:(3)【常见误区】【防范措施】
四种命题转换时的关注点
在写一个命题的其他三个命题时,应首先分清原命题的条件、结论.特别是当命题不是“若p则q”的形式,要先改变形式,再作出判断.如本例(2)就要先改写.【类题试解】在下列命题中,真命题是 ( )
A.“x=2时,x2-3x+2=0”的否命题
B.“若b=3,则b2=9”的逆命题
C.若x∈R,则x2+3<0
D.“相似三角形的对应角相等”的逆否命题【解析】选D.A选项,若x≠2,则x2-3x+2≠0,此命题是假命题,因为当x=1时,x2-3x+2=0.B选项,“若b=3,则b2=9”的逆命题为“若b2=9,则b=3”.显然是假命题.C选项,因为x2≥0,所以x2+3>0,故C选项为假命题.易知D为真命题.
四 种 命 题1.原命题与逆命题条件结论“若q,则p”2.原命题与否命题否定“若﹁p,则﹁q”3.原命题与逆否命题“若﹁q,则﹁p”否定互换1.判一判(正确的打“√”,错误的打“×”)
(1)有的命题没有逆命题.( )
(2)“对顶角相等”的否命题为“对顶角不相等”.( )
(3)原命题的否命题的逆命题就是原命题的逆否命题.( )【解析】(1)错误.任何命题都是由条件和结论构成的,所以任何命题都有逆命题.
(2)错误.“对顶角相等”的否命题为“不是对顶角的两个角不相等”.
(3)正确.原命题“若p,则q”的否命题为“若﹁p,则﹁q”,这个命题的逆命题为“若﹁q,则﹁p”,这就是原命题的逆否命题.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)若a=0,则ab=0的逆命题是 .
(2)若命题r的否命题为“若﹁p,则q”,那么原命题r为________.
(3)若a=b,则|a|=|b|的逆否命题是 .【解析】(1)逆命题只需把原命题的条件与结论互换即可,即逆命题为若ab=0,则a=0.
答案:若ab=0,则a=0
(2)因为原命题与否命题为互否命题,所以只需求“若﹁p,则q”的否命题即可,其否命题为“若p,则﹁q”.
答案:“若p,则﹁q”
(3)逆否命题既需要把原命题的条件与结论否定,又需要互换,故已知命题的逆否命题是:若|a|≠|b|,则a≠b.
答案:若|a|≠|b|,则a≠b【要点探究】
知识点 四种命题
1.原命题与逆命题
(1)逆命题是将原命题的条件与结论互换,写原命题的逆命题时,不要交换命题的前提条件.
(2)原命题的逆命题与原命题是互逆的,即逆命题的逆命题是原命题.2.原命题与否命题
(1)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.
(2)原命题也可以看作是它的否命题的否命题,即原命题与否命题是互为否命题的.
3.原命题与逆否命题
将原命题的条件和结论“换位”得逆命题,“换质”(即否定)得否命题,既“换位”又“换质”得逆否命题.【知识拓展】常见词语的否定【微思考】
(1)任何一个命题都有逆命题、否命题和逆否命题吗?
提示:因为任何一个命题都包含条件和结论两部分,通过条件和结论的不同变换都可以得到这个命题的逆命题、否命题和逆否命题.因此任何一个命题都有逆命题、否命题和逆否命题.
(2)解决四种命题转换的关键是什么?
提示:明确原命题的逆命题、否命题、逆否命题的条件和结论的位置关系和否定关系是解决四种命题的关键.【即时练】
命题p:若a=1则a2=1;命题q:若a2=1则a=1,则命题p与q的关系是 .
【解析】因为命题p与q的条件与结论正好相反,故p与q是互逆命题.
答案:互逆命题【题型示范】
类型一 写原命题的其他三种命题
【典例1】
(1)命题“两对角线相等的四边形是矩形”是命题“矩形是两条对角线相等的四边形”的( )
A.逆命题 B.否命题
C.逆否命题 D.等价命题(2)写出命题“若抛物线y=ax2+bx+c的开口向下,则集合{x|ax2+bx+c<0}≠?”的逆命题,否命题,逆否命题.【解题探究】1.题(1)中两命题的条件与结论是什么关系?
2.题(2)中命题的条件与结论各是什么?
【探究提示】1.两命题的条件与结论是互换的.
2.题(2)中命题的条件是:抛物线y=ax2+bx+c的开口向下;结论是集合{x|ax2+bx+c<0}≠?.【自主解答】(1)选A.将条件和结论互换,得到的是逆命题.故
选A.
(2)逆命题:若集合{x|ax2+bx+c<0}≠?,则抛物线y=ax2+bx+c的
开口向下.
否命题:若抛物线y=ax2+bx+c的开口向上,则集合{x|ax2+bx+c<
0}=?.
逆否命题:若集合{x|ax2+bx+c<0}=?,则抛物线y=ax2+bx+c的开
口向上.【方法技巧】四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.【变式训练】设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是( )
A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b|
C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b
【解析】选D.命题“若a=-b,则|a|=|b|”的逆命题是“若|a|=|b|,则a=-b”.故选D.【补偿训练】命题“若a>b,则a-8>b-8”的逆否命题是( )
A.若a
C.若a≤b,则a-8≤b-8 D.若a-8≤b-8,则a≤b
【解析】选D.逆否命题是将原命题中的条件和结论既交换又否定,故应选D.类型二 四种命题及其真假判断
【典例2】
(1)命题“个位数字为5的整数能被5整除”是 (填“真”或“假”)命题,它的逆命题为 ,是 (填“真”或“假”)命题.
(2)把下列命题改写成“若p,则q”的形式,并分别写出它们的逆命题、否命题与逆否命题,并判断真假:
①负数小于零.②在三角形中,大边对大角.【解题探究】1.题(1)中能被5整除的整数个位数字有什么特点?命题的条件与结论各是什么?
2.题(2)中的命题写成“若p,则q”的形式如何写?
【探究提示】1.能被5整除的整数个位数字是0或5,命题的条件是“整数的个位数字为5”,结论是“整数能被5整除”.
2.①可写为:若一个数是负数,则它小于零,
②可写为:在三角形中,若边长a最大,则它所对的角A也最大.【自主解答】(1)命题“个位数字为5的整数能被5整除”是真命题,它的逆命题为:“能被5整除的整数的个位数字为5”,如20能被5整除,个位数字为0,是假命题.
答案:真 能被5整除的整数的个位数字为5 假
(2)①原命题:若一个数是负数,则它小于零.真命题.
逆命题:若一个数小于零,则它是负数.真命题.
否命题:若一个数不是负数,则它不小于零.真命题.
逆否命题:若一个数不小于零,则它不是负数.真命题.②原命题:在三角形中,大边对大角.真命题.
逆命题:在三角形中,大角对大边.真命题.
否命题:在三角形中,不是较大的边所对的角不是较大的.真命题.
逆否命题:在三角形中,不是较大的角所对的边不是较大的.真命题.【延伸探究】本题(1)命题的否命题为 ,
是 (填“真”或“假”)命题.
【解析】题(1)命题的否命题是:个位数字不是5的整数不能被5
整除,是假命题.
答案:个位数字不是5的整数不能被5整除 假【误区警示】本题中命题的否命题易误写为“个位数字是5的整数不能被5整除”的形式,导致出现这种错误的原因是忽略了否命题既要否定结论,还要否定条件.【方法技巧】判断四种命题真假的三种技巧
技巧一:根据学过的定义、公理、定理、性质直接判断命题的真假.
技巧二:根据已知的正确的结论,通过正确地推理所得到的命题是真命题.
技巧三:判断一个命题为假时,只要能找到一个反例就够了.【变式训练】写出命题“如果一个整数的各位数字之和能被3整除,则这个整数可以被3整除”的逆命题、否命题、逆否命题,并判断其真假.
【解析】逆命题:如果一个整数可以被3整除,则这个整数的各位数字之和能被3整除.(真命题)
否命题:如果一个整数的各位数字之和不能被3整除,则这个整数不能被3整除.(真命题)
逆否命题:如果一个整数不能被3整除,则这个整数的各位数字之和不能被3整除.(真命题)【补偿训练】设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,逆命题不成立的是
( )
A.当c⊥α时,若c⊥β,则α∥β
B.当b?α时,若b⊥β,则α⊥β
C.当b?α,且c是a在α内的射影时,若b⊥c,则a⊥b
D.当b?α,且c?α时,若c∥α,则b∥c【解析】选B.A.其逆命题是:当c⊥α时,若α∥β,则c⊥β,由面面平行的性质知正确.
B.其逆命题是:当b?α时,若α⊥β,则b⊥β,由相关知识知
b与β可能垂直,也可能平行,斜交.所以B不正确.
C.其逆命题是当b?α,且c是a在α内的射影时,若a⊥b,则b⊥c,由相关知识可知正确.
D.其逆命题是当b?α,且c?α时,若b∥c,则c∥α,由线面平行的判定定理知正确,故选B.【易错误区】对命题的条件和结论分不清致误
【典例】下列说法正确的是 .
(1)“若x2+y2=0,则x,y全为零”的否命题为“若x2+y2≠0,则x,y全不为零”.
(2)“正多边形都相似”的逆命题是真命题.
(3)“若x- 是有理数,则x是无理数”的逆否命题是真命题.【解析】(1)中否命题:“若x2+y2≠0则x,y不全为0”①,故是错
误的.
(2)中逆命题:“若两个多边形相似,则这两个多边形是正多边
形”②,是假命题,故此说法错误.
(3)中逆否命题:“若x不是无理数,则x- 不是有理数”,是真
命题.故说法正确.
答案:(3)【常见误区】【防范措施】
四种命题转换时的关注点
在写一个命题的其他三个命题时,应首先分清原命题的条件、结论.特别是当命题不是“若p则q”的形式,要先改变形式,再作出判断.如本例(2)就要先改写.【类题试解】在下列命题中,真命题是 ( )
A.“x=2时,x2-3x+2=0”的否命题
B.“若b=3,则b2=9”的逆命题
C.若x∈R,则x2+3<0
D.“相似三角形的对应角相等”的逆否命题【解析】选D.A选项,若x≠2,则x2-3x+2≠0,此命题是假命题,因为当x=1时,x2-3x+2=0.B选项,“若b=3,则b2=9”的逆命题为“若b2=9,则b=3”.显然是假命题.C选项,因为x2≥0,所以x2+3>0,故C选项为假命题.易知D为真命题.
