1.2.2 充要条件 课件2
图片预览











文档简介
课件49张PPT。1.2.2
充要条件1.充要条件
(1)定义:若p?q且q?p,则记作p___q,此时p是q的充分必要条
件,简称充要条件.
(2)条件与结论的等价性:如果p是q的充要条件,那么q也是p的
_________.
2.互为充要条件
如果_____,那么p与q互为充要条件.?充要条件p?q1.判一判(正确的打“√”,错误的打“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当p成立.( )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命
题.( )
(3)若p q和q p有一个成立,则p一定不是q的充要条
件.( )【解析】(1)当p是q的充要条件时,p?q,且q?p,故说成q成立当且仅当p成立,这种说法正确.
(2)若p是q的充要条件,p?q,即p等价于q,故此说法正确.
(3)若p q或q p,则p不是q的充分条件,或p不是q的必要条件,故此说法正确.
答案:(1)√ (2)√ (3)√2.做一做(请把正确的答案写在横线上)
(1)“x2<1”的充要条件是 .
(2)若p是q的充要条件,q是r的充要条件,则p是r的 .
(3)“三角形是等边三角形”的充要条件是 .【解析】(1)因为x2<1?-1所以x2<1的充要条件是-1答案:-1(2)因为p?q,q?r,所以p?r,
所以p是r的充要条件.
答案:充要条件(3)因为“三边相等的三角形”与“三角形是等边三角形”是等价的,所以“三角形是等边三角形”的充要条件是“三角形的三边相等”.
答案:三角形的三边相等【要点探究】
知识点 充要条件
1.对充要条件的两点说明
(1)p是q的充要条件意味着“p成立,则q一定成立;
p不成立,则q一定不成立”.
(2)p是q的充要条件,则q也是p的充要条件.2.常见的四种条件与命题真假的关系
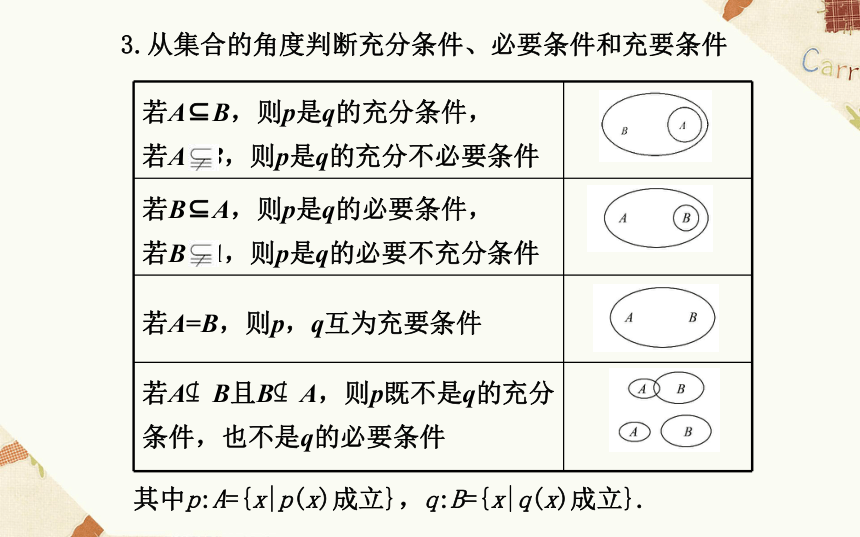
如果原命题为“若p,则q”,逆命题为“若q,则p”,那么p与q的关系有以下四种情形:3.从集合的角度判断充分条件、必要条件和充要条件其中p:A={x|p(x)成立},q:B={x|q(x)成立}.【知识拓展】等价命题的转化与充要条件
由于p是q的充要条件和p与q等价是一致的,因而我们可以通过这一结论将我们所有证明判定的结论和利用的条件进行转化,即我们可以把命题p转化为命题q来证明判定,这就是数学上重要的转化思想.【微思考】
(1)从命题的角度理解等价符号“?”的意义是什么?
提示:“?”表示连接的两个命题互为逆命题且同为真.
(2)“p是q的充要条件”与“p的充要条件是q”的区别在哪里?
提示:①p是q的充要条件说明p是条件,q是结论.
②p的充要条件是q说明q是条件,p是结论.【即时练】
1. “x>1”是“x2>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件2.向量a与非零向量b共线的充要条件为( )
A.a=0 B.a与b方向相同
C.a与b方向相反 D.存在k∈R,使a=kb【解析】1.选A.因为x2>1?x>1或x<-1,
所以x>1?x2>1,但x2>1 x>1.
故选A.
2.选D.选项A,B,C中,都是向量a与非零向量b共线的充分条件.选项D中,“存在k∈R,使a=kb”是向量a与非零向量b共线的充要条件.【题型示范】
类型一 充要条件的判断
【典例1】
(1)“m> ”是“一元二次方程x2+x+m=0无实数解”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件(2)下列所给的p,q中,p是q的充要条件的所有序号为 .
①p:x=1,q:lnx=0;②p:a2=b2,q:a=b;
③p:|x|>3,q:x2>9;④p:x>y>0,q:x2>y2.【解题探究】1.题(1)中一元二次方程x2+x+m=0有实根的条件
是什么?无实根的条件是什么?
2.题(2)中对每组的两个命题p,q,判断p是否是q的充要条件,
关键看什么?
【探究提示】1.一元二次方程x2+x+m=0有实根的条件是Δ=
1-4m≥0,即m≤ ;无实根的条件是Δ=1-4m<0,即m> .
2.关键看p能否推出q,及q能否推出p.【自主解答】(1)选B.方程x2+x+m=0无实根?Δ=1-4m<0?m> .
(2)①由于p:x=1?q:lnx=0,所以p是q的充要条件;
②由于p:a2=b2 q:a=b,所以p不是q的充要条件;
③由于p:|x|>3?q:x2>9,所以p是q的充要条件;
④由于p:x>y>0 q:x2>y2,所以p不是q的充要条件.
答案:①③【延伸探究】本例(1)中“m> ”若换为m< ,其他条件不变,
其结论又如何呢?
【解析】选D.方程x2+x+m=0无实根?Δ=1-4m<0?m> ,所以方
程x2+x+m=0无实根 m< ,
而m< 方程x2+x+m=0无实根.
所以“m< ”是“一元二次方程x2+x+m=0无实根”的既不充分
也不必要条件.【方法技巧】判断p是q的什么条件的两种思路
(1)命题角度:判断p是q的什么条件,主要是判断p?q及q?p这两个命题是否成立,若p?q成立,则p是q的充分条件,同时q是p的必要条件;若q?p成立,则p是q的必要条件,同时q是p的充分条件;若二者都成立,则p与q互为充要条件.(2)集合角度:关于充分条件、必要条件、充要条件,当不容易判断p?q及q?p的真假时,也可以从集合角度去判断,结合集合中“小集合?大集合”的关系来理解,这对解决与逻辑有关的问题是大有益处的.【变式训练】已知a,b,c∈R,问“b2=ac”是“a,b,c成等比数列”的 条件.
【解析】若b2=ac,则a,b,c不一定成等比数列,比如,a=b=c=0,
即b2=ac a,b,c成等比数列,
但是a,b,c成等比数列?b2=ac,
故是必要不充分条件.
答案:必要不充分【误区警示】解答本题易出现认为b2=ac是a,b,c成等比数列的充要条件,导致出现这种错误的原因是忽略了等比数列中每一个数不能为0.【补偿训练】设a,b,c∈R,则“ac2A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件【解析】选A.因为ac2但a比如c=0时,ac2所以是充分不必要条件.类型二 充要条件的求解与证明
【典例2】
(1)关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是 .
(2)已知ab≠0,求证a+b=1的充要条件是a3+b3+ab-a2-b2=0.【解题探究】1.题(1)中方程ax2+2x+1=0一定是一元二次方程吗?为什么?
2.题(2)中证明命题中的条件与结论各是什么?
【探究提示】1.方程ax2+2x+1=0不一定是一元二次方程.
当a=0时是一元一次方程;当a≠0时是一元二次方程.
2.命题中条件是a3+b3+ab-a2-b2=0,结论是a+b=1.【自主解答】(1)①当a=0时,原方程化为2x+1=0,此时根为
x=- ,满足条件.
②设f(x)=ax2+2x+1,当a≠0时,因为方程的常数项为1不为0,
方程没有零根.
(ⅰ)若方程有两异号的实根x1,x2,则x1x2= <0,
即a<0;(ⅱ)若方程有两个负的实根x1,x2,则需满足解得0综上,若方程至少有一个负的实根,则a≤1.
反之,若a≤1,则方程至少有一个负的实根.
因此,关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1.
答案:a≤1(2)先证必要性:因为a+b=1,
所以a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)+ab-a2-b2
=a2-ab+b2+ab-a2-b2=0,
所以必要性成立.
再证充分性:因为a3+b3+ab-a2-b2=0,
即(a+b)(a2-ab+b2)-(a2-ab+b2)=0,所以(a+b-1)(a2-ab+b2)=0.
又因为ab≠0,所以a≠0且b≠0,
从而a2-ab+b2≠0,
所以a+b-1=0,即a+b=1,故充分性成立.
所以a+b=1的充要条件是a3+b3+ab-a2-b2=0.【方法技巧】
1.求充要条件的方法
求一个问题的充要条件,就是利用等价转化的思想,使得转化前后的两个命题所对应的解集是两个相同的集合.这就要求我们转化的时候思维要缜密.2.充要条件的证明策略
(1)要证明一个条件p是否是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.
(2)在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的,证明前必须分清楚充分性和必要性,即搞清楚由哪些条件推证到哪些结论.【变式训练】关于x的方程ax2+bx+c=0有一个根为1的充要条件是什么?并证明你的结论.
【解析】因为方程ax2+bx+c=0有一个根为1,
所以a+b+c=0,
即关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0,证明如下:①充分性:
因为a+b+c=0,
所以a×12+b×1+c=0,
所以方程ax2+bx+c=0有一个根为1.
②必要性:
因为方程ax2+bx+c=0有一个根为1,
所以a×12+b×1+c=0,
所以a+b+c=0.【补偿训练】设a,b,c为△ABC的三边,求证:方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°.
【证明】充分性:
因为A=90°,所以a2=b2+c2,所以x2+2ax+b2=0可化为:
x2+2ax+a2-c2=0,
即(x+a)2-c2=0,(x+a+c)(x+a-c)=0,
所以x1=-a-c,x2=-a+c.
同理,x2+2cx-b2=0可化为:x2+2cx+c2-a2=0,即(x+c)2-a2=0,(x+a+c)(x+c-a)=0,
所以x3=-a-c,x4=a-c.所以两个方程有公共根-a-c.
必要性:
设两个方程有公共根α,则
两式相加得α2+(a+c)α=0.
若α=0,代入任一方程得b=0,这与已知a,b,c为△ABC的三边相矛盾.所以α=-a-c.代入上面方程组中任何一个式子,均可得a2=b2+c2,所以A=90°.
综上所述,关于x的方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°.【规范解答】充要条件的求解问题
【典例】(12分)求使关于x的方程x2-2mx+m2-m-2=0的两根都大于2的充要条件.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时若忽略①处Δ≥0的条件,则会导致步骤不完
整而失分.
失分点2:对第一步的条件不等价转化导致结果不正确而失
分,如将②处的条件不等价转化为 则结果显然错误.【悟题】提措施,导方向
1.等价转化的意识
对于不等式(组)的转化必须是等价的,否则求的就不是充要条
件.由“x1>2,x2>2?x1+x2>4,x1x2>4”,但反过来,“x1+x2>4,
x1x2>4 x1>2,x2>2.”例如,取x1=1,x2=5有x1+x2>4,且x1x2>4,
但没有保证两个根都大于2,所以 仅是方程的两根都
大于2的必要条件,而不是充分条件.2.整体思想的应用意识
利用一元二次方程的根与系数的关系,体现了“设而不求,整体代入”的思想和方法,如本例的化简即体现了这种思想【类题试解】求关于x的方程x2+(2m-1)x+m2=0有一个根大于1,另一个根小于1的充要条件.
【解析】令f(x)=x2+(2m-1)x+m2,因为方程x2+(2m-1)x+m2=0的一根大于1,另一根小于1,所以函数y=f(x)一个零点大于1,另一个零点小于1,如图需f(1)<0,即1+(2m-1)+m2<0,
所以m2+2m<0,所以-2故关于x的方程一根大于1,另一根小于1的充要条件是-2
充要条件1.充要条件
(1)定义:若p?q且q?p,则记作p___q,此时p是q的充分必要条
件,简称充要条件.
(2)条件与结论的等价性:如果p是q的充要条件,那么q也是p的
_________.
2.互为充要条件
如果_____,那么p与q互为充要条件.?充要条件p?q1.判一判(正确的打“√”,错误的打“×”)
(1)当p是q的充要条件时,也可说成q成立当且仅当p成立.( )
(2)若p是q的充要条件,则命题p和q是两个相互等价的命
题.( )
(3)若p q和q p有一个成立,则p一定不是q的充要条
件.( )【解析】(1)当p是q的充要条件时,p?q,且q?p,故说成q成立当且仅当p成立,这种说法正确.
(2)若p是q的充要条件,p?q,即p等价于q,故此说法正确.
(3)若p q或q p,则p不是q的充分条件,或p不是q的必要条件,故此说法正确.
答案:(1)√ (2)√ (3)√2.做一做(请把正确的答案写在横线上)
(1)“x2<1”的充要条件是 .
(2)若p是q的充要条件,q是r的充要条件,则p是r的 .
(3)“三角形是等边三角形”的充要条件是 .【解析】(1)因为x2<1?-1
所以p是r的充要条件.
答案:充要条件(3)因为“三边相等的三角形”与“三角形是等边三角形”是等价的,所以“三角形是等边三角形”的充要条件是“三角形的三边相等”.
答案:三角形的三边相等【要点探究】
知识点 充要条件
1.对充要条件的两点说明
(1)p是q的充要条件意味着“p成立,则q一定成立;
p不成立,则q一定不成立”.
(2)p是q的充要条件,则q也是p的充要条件.2.常见的四种条件与命题真假的关系
如果原命题为“若p,则q”,逆命题为“若q,则p”,那么p与q的关系有以下四种情形:3.从集合的角度判断充分条件、必要条件和充要条件其中p:A={x|p(x)成立},q:B={x|q(x)成立}.【知识拓展】等价命题的转化与充要条件
由于p是q的充要条件和p与q等价是一致的,因而我们可以通过这一结论将我们所有证明判定的结论和利用的条件进行转化,即我们可以把命题p转化为命题q来证明判定,这就是数学上重要的转化思想.【微思考】
(1)从命题的角度理解等价符号“?”的意义是什么?
提示:“?”表示连接的两个命题互为逆命题且同为真.
(2)“p是q的充要条件”与“p的充要条件是q”的区别在哪里?
提示:①p是q的充要条件说明p是条件,q是结论.
②p的充要条件是q说明q是条件,p是结论.【即时练】
1. “x>1”是“x2>1”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件2.向量a与非零向量b共线的充要条件为( )
A.a=0 B.a与b方向相同
C.a与b方向相反 D.存在k∈R,使a=kb【解析】1.选A.因为x2>1?x>1或x<-1,
所以x>1?x2>1,但x2>1 x>1.
故选A.
2.选D.选项A,B,C中,都是向量a与非零向量b共线的充分条件.选项D中,“存在k∈R,使a=kb”是向量a与非零向量b共线的充要条件.【题型示范】
类型一 充要条件的判断
【典例1】
(1)“m> ”是“一元二次方程x2+x+m=0无实数解”的( )
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件(2)下列所给的p,q中,p是q的充要条件的所有序号为 .
①p:x=1,q:lnx=0;②p:a2=b2,q:a=b;
③p:|x|>3,q:x2>9;④p:x>y>0,q:x2>y2.【解题探究】1.题(1)中一元二次方程x2+x+m=0有实根的条件
是什么?无实根的条件是什么?
2.题(2)中对每组的两个命题p,q,判断p是否是q的充要条件,
关键看什么?
【探究提示】1.一元二次方程x2+x+m=0有实根的条件是Δ=
1-4m≥0,即m≤ ;无实根的条件是Δ=1-4m<0,即m> .
2.关键看p能否推出q,及q能否推出p.【自主解答】(1)选B.方程x2+x+m=0无实根?Δ=1-4m<0?m> .
(2)①由于p:x=1?q:lnx=0,所以p是q的充要条件;
②由于p:a2=b2 q:a=b,所以p不是q的充要条件;
③由于p:|x|>3?q:x2>9,所以p是q的充要条件;
④由于p:x>y>0 q:x2>y2,所以p不是q的充要条件.
答案:①③【延伸探究】本例(1)中“m> ”若换为m< ,其他条件不变,
其结论又如何呢?
【解析】选D.方程x2+x+m=0无实根?Δ=1-4m<0?m> ,所以方
程x2+x+m=0无实根 m< ,
而m< 方程x2+x+m=0无实根.
所以“m< ”是“一元二次方程x2+x+m=0无实根”的既不充分
也不必要条件.【方法技巧】判断p是q的什么条件的两种思路
(1)命题角度:判断p是q的什么条件,主要是判断p?q及q?p这两个命题是否成立,若p?q成立,则p是q的充分条件,同时q是p的必要条件;若q?p成立,则p是q的必要条件,同时q是p的充分条件;若二者都成立,则p与q互为充要条件.(2)集合角度:关于充分条件、必要条件、充要条件,当不容易判断p?q及q?p的真假时,也可以从集合角度去判断,结合集合中“小集合?大集合”的关系来理解,这对解决与逻辑有关的问题是大有益处的.【变式训练】已知a,b,c∈R,问“b2=ac”是“a,b,c成等比数列”的 条件.
【解析】若b2=ac,则a,b,c不一定成等比数列,比如,a=b=c=0,
即b2=ac a,b,c成等比数列,
但是a,b,c成等比数列?b2=ac,
故是必要不充分条件.
答案:必要不充分【误区警示】解答本题易出现认为b2=ac是a,b,c成等比数列的充要条件,导致出现这种错误的原因是忽略了等比数列中每一个数不能为0.【补偿训练】设a,b,c∈R,则“ac2
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件【解析】选A.因为ac2
【典例2】
(1)关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是 .
(2)已知ab≠0,求证a+b=1的充要条件是a3+b3+ab-a2-b2=0.【解题探究】1.题(1)中方程ax2+2x+1=0一定是一元二次方程吗?为什么?
2.题(2)中证明命题中的条件与结论各是什么?
【探究提示】1.方程ax2+2x+1=0不一定是一元二次方程.
当a=0时是一元一次方程;当a≠0时是一元二次方程.
2.命题中条件是a3+b3+ab-a2-b2=0,结论是a+b=1.【自主解答】(1)①当a=0时,原方程化为2x+1=0,此时根为
x=- ,满足条件.
②设f(x)=ax2+2x+1,当a≠0时,因为方程的常数项为1不为0,
方程没有零根.
(ⅰ)若方程有两异号的实根x1,x2,则x1x2= <0,
即a<0;(ⅱ)若方程有两个负的实根x1,x2,则需满足解得0
反之,若a≤1,则方程至少有一个负的实根.
因此,关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1.
答案:a≤1(2)先证必要性:因为a+b=1,
所以a3+b3+ab-a2-b2
=(a+b)(a2-ab+b2)+ab-a2-b2
=a2-ab+b2+ab-a2-b2=0,
所以必要性成立.
再证充分性:因为a3+b3+ab-a2-b2=0,
即(a+b)(a2-ab+b2)-(a2-ab+b2)=0,所以(a+b-1)(a2-ab+b2)=0.
又因为ab≠0,所以a≠0且b≠0,
从而a2-ab+b2≠0,
所以a+b-1=0,即a+b=1,故充分性成立.
所以a+b=1的充要条件是a3+b3+ab-a2-b2=0.【方法技巧】
1.求充要条件的方法
求一个问题的充要条件,就是利用等价转化的思想,使得转化前后的两个命题所对应的解集是两个相同的集合.这就要求我们转化的时候思维要缜密.2.充要条件的证明策略
(1)要证明一个条件p是否是q的充要条件,需要从充分性和必要性两个方向进行,即证明两个命题“若p,则q”为真且“若q,则p”为真.
(2)在证明的过程中也可以转化为集合的思想来证明,证明p与q的解集是相同的,证明前必须分清楚充分性和必要性,即搞清楚由哪些条件推证到哪些结论.【变式训练】关于x的方程ax2+bx+c=0有一个根为1的充要条件是什么?并证明你的结论.
【解析】因为方程ax2+bx+c=0有一个根为1,
所以a+b+c=0,
即关于x的方程ax2+bx+c=0有一个根为1的充要条件是a+b+c=0,证明如下:①充分性:
因为a+b+c=0,
所以a×12+b×1+c=0,
所以方程ax2+bx+c=0有一个根为1.
②必要性:
因为方程ax2+bx+c=0有一个根为1,
所以a×12+b×1+c=0,
所以a+b+c=0.【补偿训练】设a,b,c为△ABC的三边,求证:方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°.
【证明】充分性:
因为A=90°,所以a2=b2+c2,所以x2+2ax+b2=0可化为:
x2+2ax+a2-c2=0,
即(x+a)2-c2=0,(x+a+c)(x+a-c)=0,
所以x1=-a-c,x2=-a+c.
同理,x2+2cx-b2=0可化为:x2+2cx+c2-a2=0,即(x+c)2-a2=0,(x+a+c)(x+c-a)=0,
所以x3=-a-c,x4=a-c.所以两个方程有公共根-a-c.
必要性:
设两个方程有公共根α,则
两式相加得α2+(a+c)α=0.
若α=0,代入任一方程得b=0,这与已知a,b,c为△ABC的三边相矛盾.所以α=-a-c.代入上面方程组中任何一个式子,均可得a2=b2+c2,所以A=90°.
综上所述,关于x的方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是A=90°.【规范解答】充要条件的求解问题
【典例】(12分)求使关于x的方程x2-2mx+m2-m-2=0的两根都大于2的充要条件.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时若忽略①处Δ≥0的条件,则会导致步骤不完
整而失分.
失分点2:对第一步的条件不等价转化导致结果不正确而失
分,如将②处的条件不等价转化为 则结果显然错误.【悟题】提措施,导方向
1.等价转化的意识
对于不等式(组)的转化必须是等价的,否则求的就不是充要条
件.由“x1>2,x2>2?x1+x2>4,x1x2>4”,但反过来,“x1+x2>4,
x1x2>4 x1>2,x2>2.”例如,取x1=1,x2=5有x1+x2>4,且x1x2>4,
但没有保证两个根都大于2,所以 仅是方程的两根都
大于2的必要条件,而不是充分条件.2.整体思想的应用意识
利用一元二次方程的根与系数的关系,体现了“设而不求,整体代入”的思想和方法,如本例的化简即体现了这种思想【类题试解】求关于x的方程x2+(2m-1)x+m2=0有一个根大于1,另一个根小于1的充要条件.
【解析】令f(x)=x2+(2m-1)x+m2,因为方程x2+(2m-1)x+m2=0的一根大于1,另一根小于1,所以函数y=f(x)一个零点大于1,另一个零点小于1,如图需f(1)<0,即1+(2m-1)+m2<0,
所以m2+2m<0,所以-2
