1.2.2 充要条件 课件3
图片预览






文档简介
课件16张PPT。1.2.2 充要条件高中选修《数学2-1》(新教材)复习充分条件,必要条件的定义:充分必要思考:已知p:整数a是6的倍数,
q:整数a是2和3的倍数,
那么p是q的什么条件?1、定义:称:p是q的充分必要条件,简称充要条件显然,如果p是q的充要条件,那么q也是p的充要条件p与q互为充要条件(也可以说成”p与q等价”)1、充分且必要条件
2、充分非必要条件
3、必要非充分条件
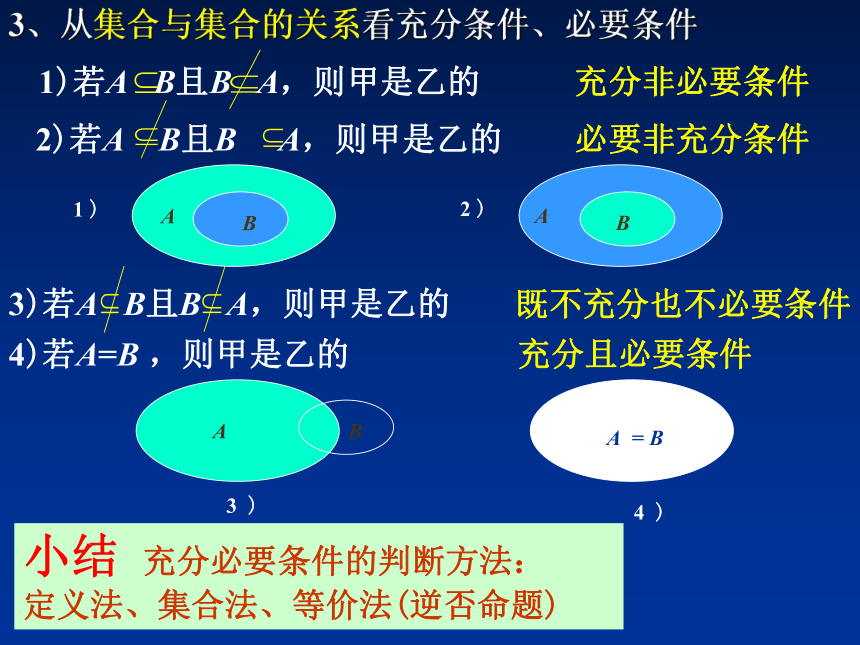
4、既不充分也不必要条件各种条件的可能情况充分非必要条件必要非充分条件既不充分也不必要条件充分且必要条件2、从逻辑推理关系看充分条件、必要条件:注:一般情况下若条件甲为x∈A,条件乙为x∈B3、从集合与集合的关系看充分条件、必要条件充分非必要条件必要非充分条件既不充分也不必要条件4)若A=B ,则甲是乙的充分且必要条件3、从集合与集合的关系看充分条件、必要条件小结 充分必要条件的判断方法:
定义法、集合法、等价法(逆否命题)例1、下列各题中,那些p是q的充要条件?
(1)p: b=0, q: 函数f(x)=ax2+bx+c是偶函数;
(2)P: x>0,y>0, q: xy>0;
(3)P: a>b, q: a+c>b+c.例2、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______ 条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________ 条件.充分不必要必要不充分充要既不充分也不必要例3.在下列电路图中,闭合开关A是灯泡B亮的什么条件:
如图(1)所示,开关A闭合是灯泡B亮的 条件;
如图(2)所示,开关A闭合是灯泡B亮的 条件;
如图(3)所示,开关A闭合是灯泡B亮的 条件;
如图(4)所示,开关A闭合是灯泡B亮的 条件;充分不必要必要不充分充要既不充分也不必要例4 已知:⊙O的半径为r,圆心O到直线L的距离为d.
求证:d=r是直线L与⊙O相切的充要条件.练习1、变.若A是B的必要而不充分条件,C是B的充
要条件,D是C的充分而不必要条件,
那么D是A的________充分不必要条件1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要不充分条件注、定义法(图形分析)必要条件充分条件必要条件3:填写“充分不必要,必要不充分,充要,既不充分又不必要.
1)sinA>sinB是A>B的_________ 条件.
2)在ΔABC中,sinA>sinB是 A>B的________条件.既不充分又不必要充要条件4、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc25、关于x的不等式:|x|+|x-1|>m的解集为R的充
要条件是( )
(A)m<0 (B)m≤0 (C)m<1 (D)m≤1 DC练习2、1、设集合M={x|x>2},N={x|x<3},那么“x∈M或x∈N”是“x∈M∩N”的( ) A.充要条件 B必要不充分条件
C充分不必要 D不充分不必要B注、集合法2、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0(转化为逆否命题)2:若┐A是┐B的充要条件,┐C是┐B的充要条件,则A为C的( )条件
A.充要 B必要不充分 C充分不必要 D不充分不必要A集合法与转化法1.已知P:|2x-3|>1;q:1/(x2+x-6)>0,
则┐p是┐q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件 2、已知p:|x+1|>2,q:x2<5x-6,
则非p是非q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件练习4、AA1.在判断条件时,要特别注意的是它们能否互相推出,切不可不加判断以单向推出代替双向推出.注意点2.搞清
①A是B的充分条件与A是B的充分非必要条件之间的区别与联系;
②A是B的必要条件与A是B的必要非充分条件之间的区别与联系3、注意几种方法的灵活使用:
定义法、集合法、逆否命题法4、判断的技巧
①向定语看齐:顺向为充(原命题真)
逆向为必(逆命题为真)
②等价性:逆否为真即为充,
否命为真即为必.练习5 求证:关于x的方程ax2+bx+c=0有一个根为1的充要条
件是a+b+c=0.【解题回顾】充要条件的证明一般分两步:
证充分性即证A =>B,证必要性即证B=>A练习6:设x、y∈R,求证|x+y|=|x|+|y|成立的充要条件是xy≥0充要条件的证明的两个方面:
1、必要性:|x+y|=|x|+|y|→xy≥0
2、充分性: xy≥0→ |x+y|=|x|+|y|
3、点明结论练习7:已知关于x的方程 (1-a)x2+(a+2)x-4=0(a∈R).
求:⑴方程有两个正根的充要条件;
⑵方程至少有一个正根的充要条件.【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件. 回顾总结:
1、条件的判断方法
定义法 集合法 等价法(逆否命题)
2、图形分析法(网)
q:整数a是2和3的倍数,
那么p是q的什么条件?1、定义:称:p是q的充分必要条件,简称充要条件显然,如果p是q的充要条件,那么q也是p的充要条件p与q互为充要条件(也可以说成”p与q等价”)1、充分且必要条件
2、充分非必要条件
3、必要非充分条件
4、既不充分也不必要条件各种条件的可能情况充分非必要条件必要非充分条件既不充分也不必要条件充分且必要条件2、从逻辑推理关系看充分条件、必要条件:注:一般情况下若条件甲为x∈A,条件乙为x∈B3、从集合与集合的关系看充分条件、必要条件充分非必要条件必要非充分条件既不充分也不必要条件4)若A=B ,则甲是乙的充分且必要条件3、从集合与集合的关系看充分条件、必要条件小结 充分必要条件的判断方法:
定义法、集合法、等价法(逆否命题)例1、下列各题中,那些p是q的充要条件?
(1)p: b=0, q: 函数f(x)=ax2+bx+c是偶函数;
(2)P: x>0,y>0, q: xy>0;
(3)P: a>b, q: a+c>b+c.例2、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______ 条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________ 条件.充分不必要必要不充分充要既不充分也不必要例3.在下列电路图中,闭合开关A是灯泡B亮的什么条件:
如图(1)所示,开关A闭合是灯泡B亮的 条件;
如图(2)所示,开关A闭合是灯泡B亮的 条件;
如图(3)所示,开关A闭合是灯泡B亮的 条件;
如图(4)所示,开关A闭合是灯泡B亮的 条件;充分不必要必要不充分充要既不充分也不必要例4 已知:⊙O的半径为r,圆心O到直线L的距离为d.
求证:d=r是直线L与⊙O相切的充要条件.练习1、变.若A是B的必要而不充分条件,C是B的充
要条件,D是C的充分而不必要条件,
那么D是A的________充分不必要条件1、已知p,q都是r的必要条件,
s是r的充分条件,q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)P是q的什么条件?充要条件充要条件必要不充分条件注、定义法(图形分析)必要条件充分条件必要条件3:填写“充分不必要,必要不充分,充要,既不充分又不必要.
1)sinA>sinB是A>B的_________ 条件.
2)在ΔABC中,sinA>sinB是 A>B的________条件.既不充分又不必要充要条件4、a>b成立的充分不必要的条件是( )
A. ac>bc B. a/c>b/c
C. a+c>b+c D. ac2>bc25、关于x的不等式:|x|+|x-1|>m的解集为R的充
要条件是( )
(A)m<0 (B)m≤0 (C)m<1 (D)m≤1 DC练习2、1、设集合M={x|x>2},N={x|x<3},那么“x∈M或x∈N”是“x∈M∩N”的( ) A.充要条件 B必要不充分条件
C充分不必要 D不充分不必要B注、集合法2、a∈R,|a|<3成立的一个必要不充分条件是( )
A.a<3 B.|a|<2 C.a2<9 D.0
A.充要 B必要不充分 C充分不必要 D不充分不必要A集合法与转化法1.已知P:|2x-3|>1;q:1/(x2+x-6)>0,
则┐p是┐q的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件 2、已知p:|x+1|>2,q:x2<5x-6,
则非p是非q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件练习4、AA1.在判断条件时,要特别注意的是它们能否互相推出,切不可不加判断以单向推出代替双向推出.注意点2.搞清
①A是B的充分条件与A是B的充分非必要条件之间的区别与联系;
②A是B的必要条件与A是B的必要非充分条件之间的区别与联系3、注意几种方法的灵活使用:
定义法、集合法、逆否命题法4、判断的技巧
①向定语看齐:顺向为充(原命题真)
逆向为必(逆命题为真)
②等价性:逆否为真即为充,
否命为真即为必.练习5 求证:关于x的方程ax2+bx+c=0有一个根为1的充要条
件是a+b+c=0.【解题回顾】充要条件的证明一般分两步:
证充分性即证A =>B,证必要性即证B=>A练习6:设x、y∈R,求证|x+y|=|x|+|y|成立的充要条件是xy≥0充要条件的证明的两个方面:
1、必要性:|x+y|=|x|+|y|→xy≥0
2、充分性: xy≥0→ |x+y|=|x|+|y|
3、点明结论练习7:已知关于x的方程 (1-a)x2+(a+2)x-4=0(a∈R).
求:⑴方程有两个正根的充要条件;
⑵方程至少有一个正根的充要条件.【解题回顾】
一是容易漏掉讨论方程二次项系数是否为零,二是只求必要条件忽略验证充分条件.即以所求的必要条件代替充要条件. 回顾总结:
1、条件的判断方法
定义法 集合法 等价法(逆否命题)
2、图形分析法(网)
