1.4 全称量词与存在量词 课件1
文档属性
| 名称 | 1.4 全称量词与存在量词 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 686.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 15:44:09 | ||
图片预览






文档简介
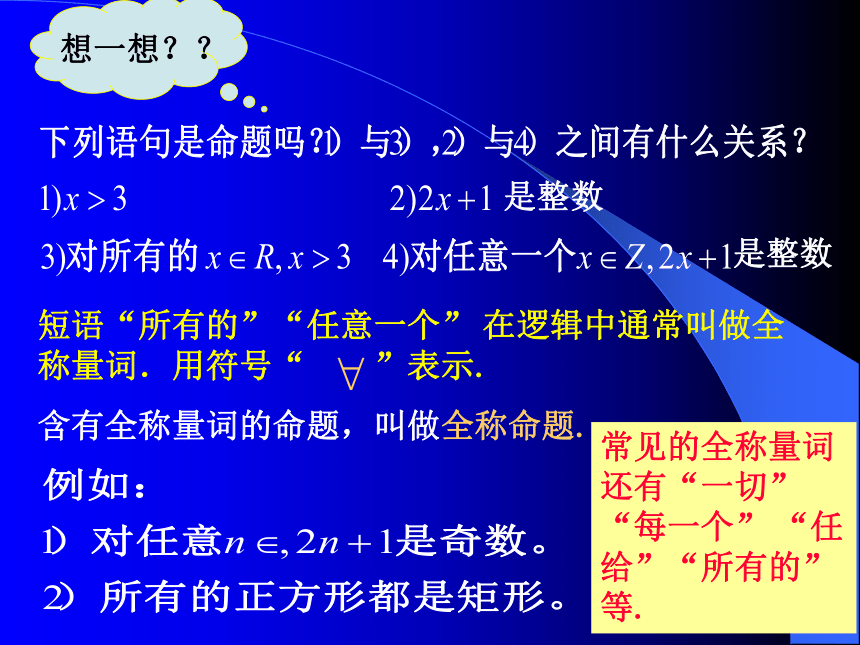
课件18张PPT。1.4全称量词 与存在量词高中选修《数学2-1》(新教材)短语“所有的”“任意一个” 在逻辑中通常叫做全称量词.用符号“ ”表示. 含有全称量词的命题,叫做全称命题.常见的全称量词还有“一切” “每一个” “任给”“所有的”等.要判断一个全称命题为真,必须对在给定集合的每一个元素x,使命题p(x)为真;但要判断一个全称命题为假时,只要在给定的集合中找到一个元素x,使命题p(x)为假. 练习:判断下列命题的真假:
(1)
(2)1.4.2 存 在 量 词短语“存在一个”“至少一个” 在逻辑中通常叫做存在量词.用符号“ ”表示. 含有存在量词的命题,叫做特称命题.常见的存在量词还有“有些” “有一个” “对某个” “有的”等.要判断一个特称命题为真,只要在给定的集合中找到一个元素x,使命题p(x)为真;要判断一个特称命题为假,必须对在给定集合的每一个元素x,使命题p(x)为假.练习:判断下列命题的真假:
(1)
(2)例、判断下列命题是全称命题,还是特称命题? (1)方程2x=5只有一解;
(2)凡是质数都是奇数;
(3)方程2x2+1=0有实数根;
(4)没有一个无理数不是实数;
(5)如果两直线不相交,则这两条直线平行;
(6)集合A∩B是集合A的子集;练习:判断下列语句是不是全称命题或者存在性命题,如果是,用量词符号表达出来. (1)中国的所有江河都注入太平洋;
(2)0不能作除数;
(3)任何一个实数除以1,仍等于这个实数;
(4)每一个向量都有方向吗?1.4.3 含有一个量词的命题
的否定含有一个量词的全称命题的否定,有下面的结论它的否定从形式看,全称命题的否定是特称命题.1)所有实数的绝对值都不是正数;2)每一个平行四边形都不是菱形;3)否定:含有一个量词的特称命题的否定,有下面的结论它的否定从形式看,特称命题的否定都变成了全称命题.含有一个量词的命题的否定全称命题的否定是特称命题,
特称命题的否定是全称命题.
(1)
(2)1.4.2 存 在 量 词短语“存在一个”“至少一个” 在逻辑中通常叫做存在量词.用符号“ ”表示. 含有存在量词的命题,叫做特称命题.常见的存在量词还有“有些” “有一个” “对某个” “有的”等.要判断一个特称命题为真,只要在给定的集合中找到一个元素x,使命题p(x)为真;要判断一个特称命题为假,必须对在给定集合的每一个元素x,使命题p(x)为假.练习:判断下列命题的真假:
(1)
(2)例、判断下列命题是全称命题,还是特称命题? (1)方程2x=5只有一解;
(2)凡是质数都是奇数;
(3)方程2x2+1=0有实数根;
(4)没有一个无理数不是实数;
(5)如果两直线不相交,则这两条直线平行;
(6)集合A∩B是集合A的子集;练习:判断下列语句是不是全称命题或者存在性命题,如果是,用量词符号表达出来. (1)中国的所有江河都注入太平洋;
(2)0不能作除数;
(3)任何一个实数除以1,仍等于这个实数;
(4)每一个向量都有方向吗?1.4.3 含有一个量词的命题
的否定含有一个量词的全称命题的否定,有下面的结论它的否定从形式看,全称命题的否定是特称命题.1)所有实数的绝对值都不是正数;2)每一个平行四边形都不是菱形;3)否定:含有一个量词的特称命题的否定,有下面的结论它的否定从形式看,特称命题的否定都变成了全称命题.含有一个量词的命题的否定全称命题的否定是特称命题,
特称命题的否定是全称命题.
