1.4.3 含有一个量词的命题的否定 课件1
文档属性
| 名称 | 1.4.3 含有一个量词的命题的否定 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 520.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 15:50:59 | ||
图片预览











文档简介
课件38张PPT。1.4.3
含有一个量词的命题的否定1.全称命题的否定?x0∈M, ?p(x0)特称2.特称命题的否定?x∈M, ?p(x)全称1.判一判(正确的打“√”,错误的打“×”)
(1)命题?p的否定是p.( )
(2)?x0∈M,p(x0)与?x∈M,?p(x)的真假性相反.( )
(3)从特称命题的否定看,是对“量词”和“p(x)”同时否定.( )【解析】(1)正确.命题p与?p互为否定.
(2)正确.特称命题p与其否定?p一真一假.
(3)错误.尽管特称命题的否定是全称命题,只是对“p(x)”进行否定,而将“存在量词”调整为“全称量词”,不能将其理解为“同时否定”.
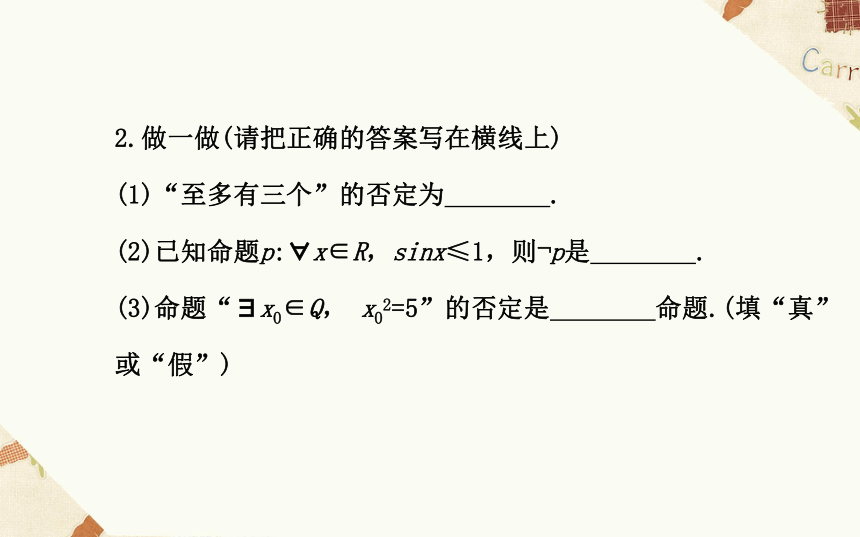
答案:(1)√ (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)“至多有三个”的否定为 .
(2)已知命题p:?x∈R,sinx≤1,则?p是 .
(3)命题“?x0∈Q, x02=5”的否定是 命题.(填“真”或“假”)【解析】(1)“至多有三个”的否定为“最少有四个”.
答案:最少有四个
(2)命题p是全称命题,其否定为?x0∈R,sinx0>1.
答案:?x0∈R,sinx0>1
(3)该命题的否定为?x∈Q,x2≠5,为真命题.
答案:真【要点探究】
知识点 全称命题与特称命题的否定
1.对全称命题的否定以及特点的理解
(1)全称命题的否定实际上是对量词“所有”否定为“并非所有”,所以全称命题的否定的等价形式就是特称命题,将全称量词调整为存在量词,就要对p(x)进行否定,这是叙述命题的需要,不能认为对全称命题进行“两次否定”,否则就是“双重否定即肯定”,所以含有一个量词的命题的否定仍是一次否定.(2)对于省去了全称量词的全称命题的否定,一般要改写为含有全称量词的命题,再写出命题的否定命题.2.对特称命题的否定以及特点的理解
(1)由于全称命题的否定是特称命题,而命题p与?p互为否定,所以特称命题的否定就是全称命题.
(2)全称命题与特称命题以及否定命题都是形式化命题,叙述命题时要结合命题的内容和特点,灵活运用自然语言、符号语言进行描述,这样才能准确判断命题的真假.【知识拓展】常见词语的否定【微思考】
(1)用自然语言描述的全称命题的否定形式惟一吗?
提示:不惟一,如“所有的菱形都是平行四边形.”它的否定是“并不是所有的菱形都是平行四边形.”也可以是“有些菱形不是平行四边形.”(2)对省略量词的命题怎样否定?
提示:一般地,省略了量词的命题是全称命题,可加上“所有的”“任意的”等一些全称量词后再进行否定.【即时练】
分别写出下列含有一个量词的命题的否定.
(1)所有的矩形都是正方形.
(2)?x0∈R, x02-2x0+1<0.
【解析】(1)将此命题中的量词“所有的”换为“存在”,然后再否定结论,即原命题的否定为:“存在一个矩形不是正方形.”
(2)此命题是特称命题,其否定为?x∈R,x2-2x+1≥0.【题型示范】
类型一 全称命题的否定与真假判断
【典例1】
(1)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:?x∈A,2x∈B,则( )
A.?p:?x0∈A,2x0∈B
B.?p:?x0?A,2x0?B
C.?p:?x0∈A,2x0?B
D.?p:?x?A,2x?B(2)写出下列全称命题的否定,并判断其否定的真假.
①p:一切分数都是有理数;
②q:直线l垂直于平面α,则对任意l′?α,l⊥l′;
③s:?x∈Q,使得 x2+ x+1是有理数.【解题探究】1.题(1)的命题p中含有的量词是什么?命题的结
论是什么?
2.题(2)各组命题中的量词是什么?命题的结论是什么?
【探究提示】1.命题p中的量词是“?”,命题的结论是
“2x∈B”.
2.命题p含有的量词是“一切”,结论为“分数都是有理数”.
命题q含有的量词是“任意”,结论为“l⊥l′”.
命题s含有的量词是“?”,结论为“ x2+ x+1是有理数”.【自主解答】(1)选C.根据题意可知命题p:?x∈A,2x∈B的否
定是?p:?x0∈A,2x0?B,故选C.
(2)①?p:存在一个分数不是有理数,假命题.
②?q:直线l垂直于平面α,则?l′0?α,使l与l′0不垂直,假
命题.
③?s:?x0∈Q,使得 + x0+1不是有理数,假命题.【延伸探究】本例(1)中的命题p若换为“?x?A,2x∈B”,其他条件不变,其结论又如何呢?
【解析】选B.将量词“?”换为“?”,结论否定即可,即其否定为:?x0?A,2x0?B”.【方法技巧】
1.对全称命题否定的两个步骤
(1)改变量词:把全称量词换为恰当的存在量词.
(2)否定性质:原命题中的“是”“成立”等改为“不是”“不成立”等.
2.全称命题否定后的真假判断方法
全称命题的否定是特称命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.【变式训练】命题“?x∈R,|x|+x2≥0”的否定是 ( )
A.?x∈R,|x|+x2<0 B.?x∈R,|x|+x2≤0
C.?x0∈R,|x0|+x02<0 D.?x0∈R,|x0|+x02≥0
【解析】选C.条件?x∈R的否定是?x0∈R,结论“|x|+x2≥0”的否定是“|x0|+x02<0”.【补偿训练】命题“?x∈R,x>sinx”的否定是( )
A.?x0∈R,x0C.?x0∈R,x0≤sinx0 D.?x∈R,x【解析】选C.命题中“?”与“?”相对,所以命题的否定是:?x0∈R,x0≤sinx0,故选C.类型二 特称命题的否定与真假判断
【典例2】
(1)命题p:“?x0∈R, x02-x0+1=0”的否定是 .
(2)写出下列特称命题的否定,并判断其否定的真假:
①有些实数的绝对值是正数;
②某些平行四边形是菱形;
③?x0∈R, x02+1<0;
④?x0,y0∈Z,使得 x0+y0=3.【解题探究】1.题(1)中命题p中含有的量词是什么?命题p的结论是什么?
2.题(2)中各命题中含有的量词是什么?各命题的结论分别是什么?【探究提示】1.命题p中含有的量词是“?”,命题的结论是
“x02-x0+1=0”.
2.命题①,②含有的量词是“有些”,“某些”,其结论分别
为:“实数的绝对值是正数”与“平行四边形是菱形”,命
题③④含有的量词是“?”,其结论分别为:“x02+1<0”与
“ x0+y0=3”.【自主解答】(1)将量词“?”换为“?”,然后否定结论即可.
答案:?x∈R,x2-x+1≠0
(2)①命题的否定是:“不存在一个实数,它的绝对值是正数”,也即“所有实数的绝对值都不是正数”.由于|-2|=2,因此命题的否定为假命题.
②命题的否定是:“没有一个平行四边形是菱形”,也即“每一个平行四边形都不是菱形”.由于菱形是平行四边形,因此命题的否定是假命题.③命题的否定是:“不存在x0∈R, x02+1<0”,也即“?x∈R,
x2+1≥0”.由于x2+1≥1>0,因此命题的否定是真命题.
④命题的否定是:“?x,y∈Z, x+y≠3”.
因为当x=0,y=3时, x+y=3,
因此命题的否定是假命题.【方法技巧】
1.对特称命题否定的两个步骤
(1)改变量词:把存在量词换为恰当的全称量词.
(2)否定性质:原命题中的“有”“存在”等更改为“没有” “不存在”等.
2.特称命题否定后的真假判断
特称命题的否定是全称命题,其真假性与特称命题相反;要说明一个特称命题是真命题,只需要找到一个实例即可.【变式训练】写出下列特称命题的否定,并判断其真假.
(1)存在x0>1,使x02-2x0-3=0.
(2)若an=-2n+1,则存在n0∈N,使 <0.
(3)存在x0∈R,x0>2.
(4)存在x0∈R, x02<0.【解析】(1)任意x>1,x2-2x-3≠0,假命题.
(2)若an=-2n+1,则任意n∈N,Sn≥0,假命题.
(3)任意x∈R有x≤2,假命题.
(4)任意x∈R,x2≥0,真命题.【补偿训练】写出下列特称命题p的否定?p,并判断?p的真假:
(1)p:?x0<0, x02<0.
(2)p:?α0,β0∈R,cos(α0+β0)=cosα0+cosβ0.
(3)p:有些数列既是等差数列又是等比数列.【解析】(1)?p:?x<0,x2≥0.真命题.
(2)?p:?α,β∈R,cos(α+β)≠cosα+cosβ.
由于当α= ,β= 时,cos(α+β)=cosα+cosβ=
所以?p为假命题.
(3)?p:任何数列都不能既是等差数列又是等比数列.
由于非零常数列既是等差数列又是等比数列,所以?p为假命题.【易错误区】混淆命题的否定与否命题而致误
【典例】命题“任意x∈R,若y>0,则x2+y>0”的否定是 .【解析】已知命题是一个全称命题,其否定为特称命题,先将
“任意”换成“存在”再否定结论,
即命题的否定是:
存在x0∈R,
若y>0,则x02+y≤0.
答案:存在x0∈R,若y>0,则x02+y≤0【常见误区】【防范措施】
命题的否定与否命题
命题的否定只否定结论.否命题是条件和结论都要否定,如本例中命题的否定,否定结论没有否定条件.【类题试解】命题p:任意x,y∈R,若x>y,则x2>y2,则命题p的否定为 ,否命题为 .
【解析】命题p的否定为:存在x0,y0∈R,若x0>y0,则
否命题为:任意x,y∈R,若x≤y,则x2≤y2.
答案:存在x0,y0∈R,若x0>y0,则
任意x,y∈R,若x≤y,则x2≤y2
含有一个量词的命题的否定1.全称命题的否定?x0∈M, ?p(x0)特称2.特称命题的否定?x∈M, ?p(x)全称1.判一判(正确的打“√”,错误的打“×”)
(1)命题?p的否定是p.( )
(2)?x0∈M,p(x0)与?x∈M,?p(x)的真假性相反.( )
(3)从特称命题的否定看,是对“量词”和“p(x)”同时否定.( )【解析】(1)正确.命题p与?p互为否定.
(2)正确.特称命题p与其否定?p一真一假.
(3)错误.尽管特称命题的否定是全称命题,只是对“p(x)”进行否定,而将“存在量词”调整为“全称量词”,不能将其理解为“同时否定”.
答案:(1)√ (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)“至多有三个”的否定为 .
(2)已知命题p:?x∈R,sinx≤1,则?p是 .
(3)命题“?x0∈Q, x02=5”的否定是 命题.(填“真”或“假”)【解析】(1)“至多有三个”的否定为“最少有四个”.
答案:最少有四个
(2)命题p是全称命题,其否定为?x0∈R,sinx0>1.
答案:?x0∈R,sinx0>1
(3)该命题的否定为?x∈Q,x2≠5,为真命题.
答案:真【要点探究】
知识点 全称命题与特称命题的否定
1.对全称命题的否定以及特点的理解
(1)全称命题的否定实际上是对量词“所有”否定为“并非所有”,所以全称命题的否定的等价形式就是特称命题,将全称量词调整为存在量词,就要对p(x)进行否定,这是叙述命题的需要,不能认为对全称命题进行“两次否定”,否则就是“双重否定即肯定”,所以含有一个量词的命题的否定仍是一次否定.(2)对于省去了全称量词的全称命题的否定,一般要改写为含有全称量词的命题,再写出命题的否定命题.2.对特称命题的否定以及特点的理解
(1)由于全称命题的否定是特称命题,而命题p与?p互为否定,所以特称命题的否定就是全称命题.
(2)全称命题与特称命题以及否定命题都是形式化命题,叙述命题时要结合命题的内容和特点,灵活运用自然语言、符号语言进行描述,这样才能准确判断命题的真假.【知识拓展】常见词语的否定【微思考】
(1)用自然语言描述的全称命题的否定形式惟一吗?
提示:不惟一,如“所有的菱形都是平行四边形.”它的否定是“并不是所有的菱形都是平行四边形.”也可以是“有些菱形不是平行四边形.”(2)对省略量词的命题怎样否定?
提示:一般地,省略了量词的命题是全称命题,可加上“所有的”“任意的”等一些全称量词后再进行否定.【即时练】
分别写出下列含有一个量词的命题的否定.
(1)所有的矩形都是正方形.
(2)?x0∈R, x02-2x0+1<0.
【解析】(1)将此命题中的量词“所有的”换为“存在”,然后再否定结论,即原命题的否定为:“存在一个矩形不是正方形.”
(2)此命题是特称命题,其否定为?x∈R,x2-2x+1≥0.【题型示范】
类型一 全称命题的否定与真假判断
【典例1】
(1)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:?x∈A,2x∈B,则( )
A.?p:?x0∈A,2x0∈B
B.?p:?x0?A,2x0?B
C.?p:?x0∈A,2x0?B
D.?p:?x?A,2x?B(2)写出下列全称命题的否定,并判断其否定的真假.
①p:一切分数都是有理数;
②q:直线l垂直于平面α,则对任意l′?α,l⊥l′;
③s:?x∈Q,使得 x2+ x+1是有理数.【解题探究】1.题(1)的命题p中含有的量词是什么?命题的结
论是什么?
2.题(2)各组命题中的量词是什么?命题的结论是什么?
【探究提示】1.命题p中的量词是“?”,命题的结论是
“2x∈B”.
2.命题p含有的量词是“一切”,结论为“分数都是有理数”.
命题q含有的量词是“任意”,结论为“l⊥l′”.
命题s含有的量词是“?”,结论为“ x2+ x+1是有理数”.【自主解答】(1)选C.根据题意可知命题p:?x∈A,2x∈B的否
定是?p:?x0∈A,2x0?B,故选C.
(2)①?p:存在一个分数不是有理数,假命题.
②?q:直线l垂直于平面α,则?l′0?α,使l与l′0不垂直,假
命题.
③?s:?x0∈Q,使得 + x0+1不是有理数,假命题.【延伸探究】本例(1)中的命题p若换为“?x?A,2x∈B”,其他条件不变,其结论又如何呢?
【解析】选B.将量词“?”换为“?”,结论否定即可,即其否定为:?x0?A,2x0?B”.【方法技巧】
1.对全称命题否定的两个步骤
(1)改变量词:把全称量词换为恰当的存在量词.
(2)否定性质:原命题中的“是”“成立”等改为“不是”“不成立”等.
2.全称命题否定后的真假判断方法
全称命题的否定是特称命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.【变式训练】命题“?x∈R,|x|+x2≥0”的否定是 ( )
A.?x∈R,|x|+x2<0 B.?x∈R,|x|+x2≤0
C.?x0∈R,|x0|+x02<0 D.?x0∈R,|x0|+x02≥0
【解析】选C.条件?x∈R的否定是?x0∈R,结论“|x|+x2≥0”的否定是“|x0|+x02<0”.【补偿训练】命题“?x∈R,x>sinx”的否定是( )
A.?x0∈R,x0
【典例2】
(1)命题p:“?x0∈R, x02-x0+1=0”的否定是 .
(2)写出下列特称命题的否定,并判断其否定的真假:
①有些实数的绝对值是正数;
②某些平行四边形是菱形;
③?x0∈R, x02+1<0;
④?x0,y0∈Z,使得 x0+y0=3.【解题探究】1.题(1)中命题p中含有的量词是什么?命题p的结论是什么?
2.题(2)中各命题中含有的量词是什么?各命题的结论分别是什么?【探究提示】1.命题p中含有的量词是“?”,命题的结论是
“x02-x0+1=0”.
2.命题①,②含有的量词是“有些”,“某些”,其结论分别
为:“实数的绝对值是正数”与“平行四边形是菱形”,命
题③④含有的量词是“?”,其结论分别为:“x02+1<0”与
“ x0+y0=3”.【自主解答】(1)将量词“?”换为“?”,然后否定结论即可.
答案:?x∈R,x2-x+1≠0
(2)①命题的否定是:“不存在一个实数,它的绝对值是正数”,也即“所有实数的绝对值都不是正数”.由于|-2|=2,因此命题的否定为假命题.
②命题的否定是:“没有一个平行四边形是菱形”,也即“每一个平行四边形都不是菱形”.由于菱形是平行四边形,因此命题的否定是假命题.③命题的否定是:“不存在x0∈R, x02+1<0”,也即“?x∈R,
x2+1≥0”.由于x2+1≥1>0,因此命题的否定是真命题.
④命题的否定是:“?x,y∈Z, x+y≠3”.
因为当x=0,y=3时, x+y=3,
因此命题的否定是假命题.【方法技巧】
1.对特称命题否定的两个步骤
(1)改变量词:把存在量词换为恰当的全称量词.
(2)否定性质:原命题中的“有”“存在”等更改为“没有” “不存在”等.
2.特称命题否定后的真假判断
特称命题的否定是全称命题,其真假性与特称命题相反;要说明一个特称命题是真命题,只需要找到一个实例即可.【变式训练】写出下列特称命题的否定,并判断其真假.
(1)存在x0>1,使x02-2x0-3=0.
(2)若an=-2n+1,则存在n0∈N,使 <0.
(3)存在x0∈R,x0>2.
(4)存在x0∈R, x02<0.【解析】(1)任意x>1,x2-2x-3≠0,假命题.
(2)若an=-2n+1,则任意n∈N,Sn≥0,假命题.
(3)任意x∈R有x≤2,假命题.
(4)任意x∈R,x2≥0,真命题.【补偿训练】写出下列特称命题p的否定?p,并判断?p的真假:
(1)p:?x0<0, x02<0.
(2)p:?α0,β0∈R,cos(α0+β0)=cosα0+cosβ0.
(3)p:有些数列既是等差数列又是等比数列.【解析】(1)?p:?x<0,x2≥0.真命题.
(2)?p:?α,β∈R,cos(α+β)≠cosα+cosβ.
由于当α= ,β= 时,cos(α+β)=cosα+cosβ=
所以?p为假命题.
(3)?p:任何数列都不能既是等差数列又是等比数列.
由于非零常数列既是等差数列又是等比数列,所以?p为假命题.【易错误区】混淆命题的否定与否命题而致误
【典例】命题“任意x∈R,若y>0,则x2+y>0”的否定是 .【解析】已知命题是一个全称命题,其否定为特称命题,先将
“任意”换成“存在”再否定结论,
即命题的否定是:
存在x0∈R,
若y>0,则x02+y≤0.
答案:存在x0∈R,若y>0,则x02+y≤0【常见误区】【防范措施】
命题的否定与否命题
命题的否定只否定结论.否命题是条件和结论都要否定,如本例中命题的否定,否定结论没有否定条件.【类题试解】命题p:任意x,y∈R,若x>y,则x2>y2,则命题p的否定为 ,否命题为 .
【解析】命题p的否定为:存在x0,y0∈R,若x0>y0,则
否命题为:任意x,y∈R,若x≤y,则x2≤y2.
答案:存在x0,y0∈R,若x0>y0,则
任意x,y∈R,若x≤y,则x2≤y2
