2.1.2 求曲线的方程 课件2
文档属性
| 名称 | 2.1.2 求曲线的方程 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览




文档简介
课件11张PPT。2.1.2 求曲线的方程1zxxkw 则这个方程就叫做曲线的方程,这条曲线就叫做方程的曲线. 1.曲线的方程、方程的曲线的定义:一.复习引入(1)曲线上点的坐标都是方程的解;
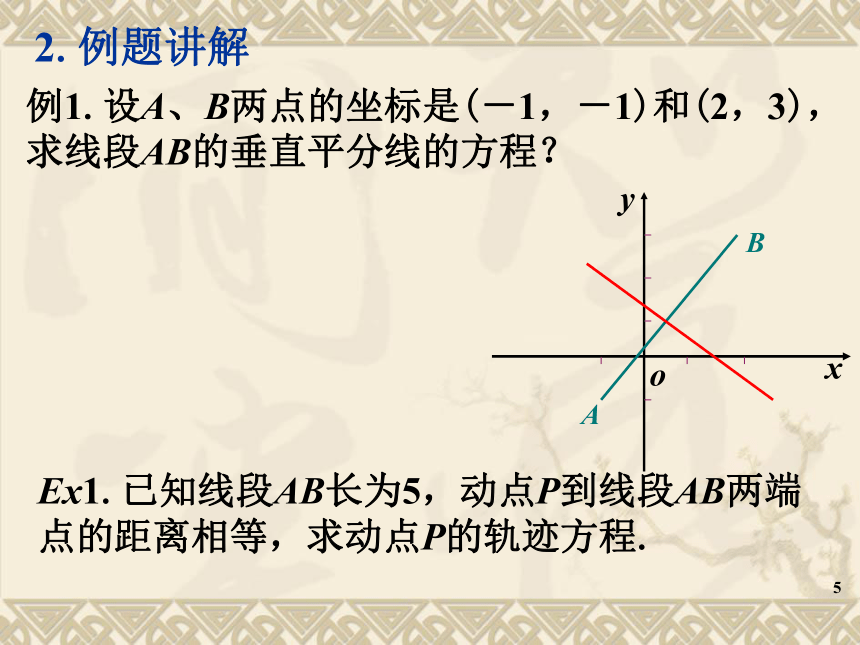
(2)以方程的解为坐标的点都在曲线上.12.解析几何有两类问题:一是利用曲线求方程;二是利用方程研究曲线的性质.其中最基本的方法是坐标法.1二.新课1. 如何求曲线(点的轨迹)方程?求曲线方程的实质是将产生曲线的几何条件逐步转化为含动点坐标的代数方程的过程. 在直角坐标系下:12.例题讲解例1.设A、B两点的坐标是(-1,-1)和(2,3),求线段AB的垂直平分线的方程?Ex1.已知线段AB长为5,动点P到线段AB两端点的距离相等,求动点P的轨迹方程.1求曲线方程的一般步骤:1.建系设点:建立适当的直角坐标系,用有序实数
对(x,y)表示曲线上任一点M的坐标;(如果题目中已确定坐标系就不必再建立)2.寻找条件:写出适合条件P的点M的集合; P={M︱p(M)},3.列出方程:用坐标表示条件p(M),列出
方程f(x,y)=0;4.化简:化方程f(x,y)=0为最简形式;5.检验:检验以化简后的方程的解为坐标的点都是
曲线上的点.1Ex2.△ABC顶点B、C的坐标分别是(0,0)和(4,0),
BC边上的中线长为3,求顶点A的轨迹方程. 以这个方程的解为坐标的点是否都在曲线上?思考?(x-2)2+y2=9 (x≠5且x≠-1)D1求曲线方程的一般步骤:1.建系设点:建立适当的直角坐标系,用有序实数
对(x,y)表示曲线上任一点M的坐标;2.寻找条件:写出适合条件P的点M的集合;3.列出方程:用坐标表示条件p(M),列出
方程f(x,y)=0;4.化简:化方程f(x,y)=0为最简形式;5.检验:检验以化简后的方程的解为坐标的点都是
曲线上的点.检验是否产生增解或漏解1Ex4.已知点C到直线L的距离为8,若动点P到点C和
直线L的距离相等,求动点P的轨迹方程.1建立坐标系的原则: 1.建立的坐标系有利于求出题目的结果;2.尽可能多的使图形上的点(或已知点),落在坐标轴上;3.充分利用图形本身的对称性;若曲线是轴对称图形,则可以选它的对称轴为坐
标轴,也可以选取曲线上的特殊点为坐标原点.4.保持图形整体性.1三.归纳与小结1
(2)以方程的解为坐标的点都在曲线上.12.解析几何有两类问题:一是利用曲线求方程;二是利用方程研究曲线的性质.其中最基本的方法是坐标法.1二.新课1. 如何求曲线(点的轨迹)方程?求曲线方程的实质是将产生曲线的几何条件逐步转化为含动点坐标的代数方程的过程. 在直角坐标系下:12.例题讲解例1.设A、B两点的坐标是(-1,-1)和(2,3),求线段AB的垂直平分线的方程?Ex1.已知线段AB长为5,动点P到线段AB两端点的距离相等,求动点P的轨迹方程.1求曲线方程的一般步骤:1.建系设点:建立适当的直角坐标系,用有序实数
对(x,y)表示曲线上任一点M的坐标;(如果题目中已确定坐标系就不必再建立)2.寻找条件:写出适合条件P的点M的集合; P={M︱p(M)},3.列出方程:用坐标表示条件p(M),列出
方程f(x,y)=0;4.化简:化方程f(x,y)=0为最简形式;5.检验:检验以化简后的方程的解为坐标的点都是
曲线上的点.1Ex2.△ABC顶点B、C的坐标分别是(0,0)和(4,0),
BC边上的中线长为3,求顶点A的轨迹方程. 以这个方程的解为坐标的点是否都在曲线上?思考?(x-2)2+y2=9 (x≠5且x≠-1)D1求曲线方程的一般步骤:1.建系设点:建立适当的直角坐标系,用有序实数
对(x,y)表示曲线上任一点M的坐标;2.寻找条件:写出适合条件P的点M的集合;3.列出方程:用坐标表示条件p(M),列出
方程f(x,y)=0;4.化简:化方程f(x,y)=0为最简形式;5.检验:检验以化简后的方程的解为坐标的点都是
曲线上的点.检验是否产生增解或漏解1Ex4.已知点C到直线L的距离为8,若动点P到点C和
直线L的距离相等,求动点P的轨迹方程.1建立坐标系的原则: 1.建立的坐标系有利于求出题目的结果;2.尽可能多的使图形上的点(或已知点),落在坐标轴上;3.充分利用图形本身的对称性;若曲线是轴对称图形,则可以选它的对称轴为坐
标轴,也可以选取曲线上的特殊点为坐标原点.4.保持图形整体性.1三.归纳与小结1
