2.2.1 椭圆及其标准方程 课件5
文档属性
| 名称 | 2.2.1 椭圆及其标准方程 课件5 |  | |
| 格式 | zip | ||
| 文件大小 | 821.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 17:13:55 | ||
图片预览







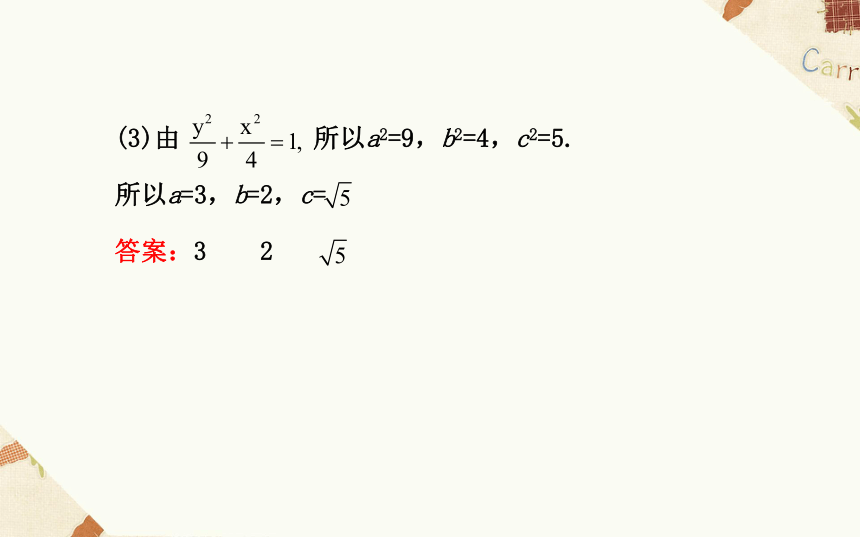



文档简介
课件60张PPT。2.2 椭 圆
2.2.1 椭圆及其标准方程1.椭圆的定义
(1)定义:平面内与两个定点F1,F2的距离之和等于_____(大于
|F1F2|)的点的轨迹.
(2)焦点:两个定点F1,F2.
(3)焦距:两焦点间的距离|F1F2|.
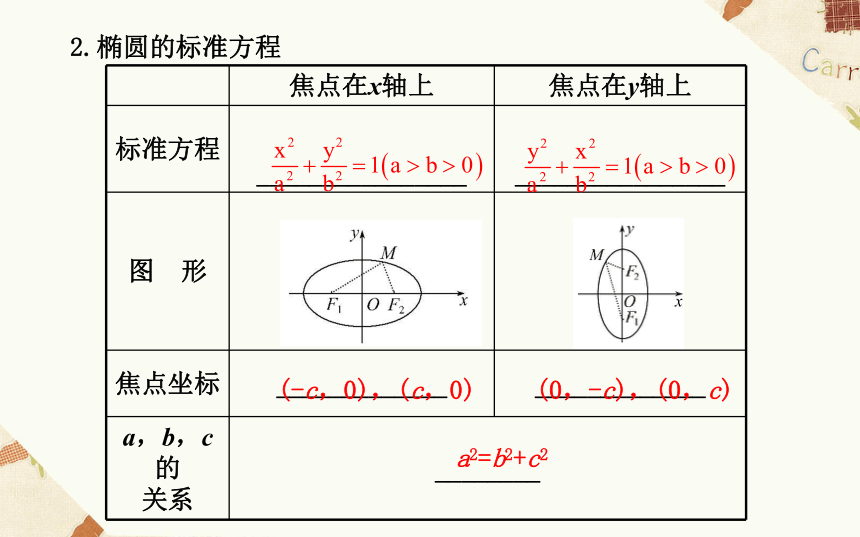
(4)几何表示:|MF1|+|MF2|=___(常数)且2a__|F1F2|.常数2a>2.椭圆的标准方程(-c,0),(c,0)(0,-c),(0,c)a2=b2+c21.判一判(正确的打“√”,错误的打“×”)
(1)椭圆的两种标准方程中,虽然焦点位置不同,但都有a2=b2+c2.( )
(2)平面内到两个定点F1,F2的距离之和等于常数的点的集合是椭圆.( )
(3)椭圆的特殊形式是圆.( )【解析】(1)正确.无论在哪种标准方程中,一定都有a2=b2+c2.
(2)错误.只有常数大于|F1F2|时,点的集合才是椭圆.
(3)错误.椭圆与圆的概念不同,没有特殊情况.
答案:(1)√ (2)× (3)×2.做一做(请把正确的答案写在横线上)
(1)a=5,c=3,焦点在x轴上的椭圆标准方程为 .
(2)方程4x2+9y2=1的焦点坐标为 .
(3)椭圆的方程为 则a= ,b= ,
c= .【解析】(1)由a2=b2+c2,得b2=52-32=42=16,
所以椭圆的方程为
答案:
(2)由4x2+9y2=1,得 所以
所以焦点坐标为
答案:(3)由 所以a2=9,b2=4,c2=5.
所以a=3,b=2,c=
答案:3 2【要点探究】
知识点 1 椭圆的定义
1.对椭圆定义的三点说明
(1)椭圆是在平面内定义的,所以“平面内”这一条件不能视.
(2)定义中到两定点的距离之和是常数,而不能是变量.
(3)常数(2a)必须大于两定点间的距离,否则轨迹不是椭圆,这是判断一曲线是否为椭圆的限制条件.2.椭圆定义的两个应用
(1)若|MF1|+|MF2|=2a(2a>|F1F2|),则动点M的轨迹是椭圆.
(2)若点M在椭圆上,则|MF1|+|MF2|=2a.【知识拓展】椭圆的焦点三角形
设M为椭圆 上任意一点
(不在x轴上).F1,F2为焦点,则
△MF1F2为椭圆的焦点三角形.【微思考】
在椭圆的定义中,动点M到两定点F1,F2的距离之和等于常数(2a)且2a>|F1F2|,若2a=|F1F2|,则M的轨迹是什么?若2a<|F1F2|,则M的轨迹是什么?
提示:当2a=|F1F2|时,点M的轨迹是线段F1F2;
当2a<|F1F2|时,点M的轨迹不存在.【即时练】
1.椭圆 的左、右焦点分别为F1,F2,点P在椭圆上,
若|PF1|=4,则|PF2|=________.
2.已知椭圆 的两焦点为F1,F2,弦AB过点F1,则
△ABF2的周长为_________.【解析】1.由椭圆的定义知|PF1|+|PF2|=6,
所以|PF2|=6-|PF1|=6-4=2.
答案:2
2.由椭圆的定义知2a=10,
△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|AF2|+|BF1|+|BF2|=4a=20.
答案:20知识点 2 椭圆的标准方程
对椭圆标准方程的三点认识
(1)标准方程的几何特征:椭圆的中心在坐标原点,焦点在x轴或
y轴上.
(2)标准方程的代数特征:方程右边为1,左边是关于 的
平方和,并且分母为不相等的正值.(3)a,b,c三个量的关系:椭圆的标准方程中,
a表示椭圆上的点M到两焦点间距离的和的一
半,可借助图形帮助记忆.a,b,c(都是正数)
恰是构成一个直角三角形的三条边,a是斜边,所以a>b,a>c,且a2=b2+c2.(如图所示)【微思考】
(1)在椭圆的标准方程中a>b>c一定成立吗?
提示:不一定,只要a>b,a>c即可,b,c大小关系不定.
(2)根据椭圆方程,如何确定焦点位置?
提示:把方程化为标准形式,x2,y2的分母哪个大,焦点就在相应的轴上.【即时练】
椭圆25x2+16y2=400的焦点坐标为 ,焦距为_______.
【解析】把方程化为标准式:
可知焦点在y轴上,
则a2=25,b2=16,所以c2=25-16=9,
则c=3,所以焦点为(0,±3),焦距为2c=6.
答案:(0,±3) 6 【题型示范】
类型一 求椭圆的标准方程
【典例1】
(1)过点(-3,2)且与 有相同
焦点的椭圆的方程是( )(2)求适合下列条件的椭圆的标准方程:
①两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0).
②焦点在y轴上,且经过两个点(0,2)和(1,0).
③经过点 和点【解题探究】1.题(1)焦点在哪个轴上?
2.题①焦点在x轴上的椭圆的标准方程是怎样的?
题②焦点在y轴上的椭圆的标准方程是怎样的?
题③焦点位置不确定,椭圆的标准方程应如何求?【探究提示】1.椭圆的焦点在x轴上,因为已知方程中x2项的分母较大.
2.① (a>b>0);
② (a>b>0);
③应分焦点在x轴上,y轴上两种情况讨论求解.【自主解答】(1)选A.由方程 可知,其焦点的坐标为
即
设所求椭圆方程为 (a>b>0).
因为过点(-3,2),代入方程为 解得a2=15(a2=3舍去).
故方程为(2)①由于椭圆的焦点在x轴上,
所以设它的标准方程为 (a>b>0).
因为 所以a=5.
又c=4,所以b2=a2-c2=25-16=9.
故所求椭圆的标准方程为②由于椭圆的焦点在y轴上,
所以设它的标准方程为 (a>b>0).
由于椭圆经过点(0,2)和(1,0),
所以
故所求椭圆的标准方程为③方法一:当焦点在x轴上时,
设椭圆的标准方程为 (a>b>0).
依题意有 解得
故所求椭圆的标准方程为当焦点在y轴上时,设椭圆的标准方程为 (a>b>0).
依题意有 解得
因为a>b>0,所以无解.
综上,所求椭圆的标准方程为方法二:设所求椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n),
依题意有 解得
所以所求的椭圆方程为:【方法技巧】
1.求椭圆方程的方法2.椭圆方程的设法技巧
若椭圆的焦点位置不确定,需要分焦点在x轴上和在y轴上两种情况讨论,也可设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n).【变式训练】求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-2,0),(2,0),椭圆上一点P到两焦点距离之和等于6,求椭圆的方程.
(2)椭圆的焦点为F1(0,-5),F2(0,5),点P(3,4)是椭圆上的一个点,求椭圆的方程.【解析】(1)由椭圆的焦点坐标为(-2,0),(2,0),
所以可设椭圆的方程为: (a>b>0).
因为2a=6,2c=4,所以a=3,c=2,
所以b2=a2-c2=5,
所以所求点的轨迹方程为:(2)因为焦点为F1(0,-5),F2(0,5),可设椭圆方程为
2a=
所以a= c=5,b2=40-25=15,
所以椭圆方程为【补偿训练】已知椭圆 (a>b>0)上一点P(3,4),
且两焦点分别为F1,F2,若PF1⊥PF2,试求椭圆方程.
【解题指南】由PF1⊥PF2,可得出 求出c的值.再
根据点P在椭圆上,且a2=b2+c2,建立a,b的方程组,求出a,b的
值.【解析】因为椭圆经过点P(3,4),
所以
又a2=b2+c2, ②
设F1(-c,0),F2(c,0),
则
因为PF1⊥PF2,
所以所以
即9-c2=-16.
所以c2=25.所以c=5.
由①②可得
所以a2=45,b2=20.
故所求椭圆方程为类型二 与椭圆有关的轨迹问题
【典例2】
(1)已知点M在椭圆 上,MP′垂直于椭圆焦点所在的
直线,垂足为P′,并且M为线段PP′的中点,则P点的轨迹方
程为________.
(2)(2013·新课标全国卷Ⅰ改编)已知圆M:(x+1)2+y2=1,圆
N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹
为曲线C.求C的方程.【解题探究】1.题(1)动点P与哪个动点有关?本题可采用什么方法求动点P的轨迹方程?
2.两圆外切时能得到什么条件?内切时能得到什么条件?
【探究提示】1.动点P与点M有关.因为点M在已知椭圆上运动,所以本题可采用代入法求动点P的轨迹方程.
2.两圆外切,两圆的圆心距等于半径之和;两圆内切,两圆的圆心距等于半径差的绝对值.【自主解答】(1)设点P的坐标为(x,y),M点的坐标为(x0,y0).
因为点M在椭圆 上,所以
因为M是线段PP′的中点,所以
把 代入 得
即x2+y2=36.
所以点P的轨迹方程为x2+y2=36.
答案:x2+y2=36(2)由已知得圆M的圆心为M(-1,0),半径r1=1;圆N的圆心为
N(1,0),半径r2=3.设圆P的圆心为P(x,y),半径为R.动圆P与圆
M外切并且与圆N内切,
所以|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4.
由椭圆定义可知,曲线C是以M,N为左、右焦点,长半轴长为
2,短半轴长为 的椭圆(左顶点除外),其方程为
(x≠-2).【方法技巧】求解与椭圆相关的轨迹问题的方法【变式训练】已知两定点F1(-1,0),F2(1,0),且|F1F2|是|PF1|与|PF2|的等差中项,则动点P的轨迹方程是( )【解析】选C.因为|F1F2|是|PF1|和|PF2|的等差中项,
所以|PF1|+|PF2|=2|F1F2|=2×2=4>|F1F2|.
所以P的轨迹应是以F1,F2为焦点的椭圆.
这里c=1,a=2.
所以轨迹方程为【补偿训练】求过点P(3,0)且与圆x2+6x+y2-91=0相内切的动
圆圆心的轨迹方程.
【解析】圆方程配方整理得(x+3)2+y2=102,圆心为C1(-3,0),半
径为R=10.设所求动圆圆心为C(x,y),半径为r,依题意有
消去r得R-|PC|=|CC1|?|PC|+
|CC1|=R,即|PC|+|CC1|=10.又P(3,0),C1(-3,0),且|PC1|=6<10.可见C点是以P,C1为两焦点的椭圆,且c=3,2a=10,
所以a=5,从而b=4,
故所求的动圆圆心的轨迹方程为类型三 求参数的取值范围
【典例3】
(1)已知方程 表示焦点在y轴上的椭圆,则m的
取值范围为__________.
(2) 已知x2sin α+y2cos α=1(0≤α≤π)表示焦点在x轴上的椭圆.求α的取值范围.【解题探究】1.题(1)已知椭圆标准方程为 其中m,n
应满足什么条件?
2.题(2)如何将x2sin α+y2cos α=1化成标准形式?【探究提示】1.m,n应满足条件 若焦点在x轴上,应有
m>n;若焦点在y轴上,应有m<n.
2.当sin α≠0,cos α≠0时,方程x2sin α+y2cos α=1可
化为【自主解答】(1)由题意得: 即
所以
答案:(2)由题意可将已知方程化为
因为椭圆的焦点在x轴上,
所以 即
又因为0≤α≤π,所以
即所求α的取值范围是【延伸探究】若把题(1)中方程改为 其余条件
不变,求m的取值范围.
【解析】由题意得
①当m>0时,
所以②当m<0时, 所以m<-1.
所以m的取值范围是【方法技巧】求参数取值范围的方法
(1)求参数的范围就是根据条件列出参数为未知量的不等式(组)或方程(组),把问题转化为不等式(组)或方程(组)的求解问题.
(2)对于椭圆,如果焦点所在的位置不确定,就需分两种情况分别列式求解. 【变式训练】椭圆5x2+ky2=5的一个焦点是(0,2),那么实数k的值为( )
A.-25 B.25 C.-1 D.1
【解析】选D.由5x2+ky2=5,得 因为一个焦点是
(0,2),所以 得k=1.【补偿训练】如果方程 表示焦点在x轴上的椭圆,
则实数a的取值范围是( )
A.a>3 B.a<-2
C.a<-2或a>3 D.-6<a<-2或a>3
【解析】选D.因为方程 表示焦点在x轴上的椭圆,
所以有
解得a>3或-6<a<-2.【易错误区】对椭圆标准方程理解不清致误
【典例】若方程 表示椭圆,则m满足的条件是
_______.
【解析】由方程 表示椭圆,
知 解得 且m≠1.
答案:【常见误区】【防范措施】
牢记标准方程的特点
必须明确形如方程 表示椭圆、圆的条件,如本例中,
方程表示椭圆.首先应满足A≠B,其次应有A>0,B>0,事实上,当
A=B时,方程表示的曲线为圆而非椭圆.【类题试解】若方程 表
示椭圆,则实数k的取值范围是________.
【解析】由方程 表示椭圆,可得
解得2<k<5且
即当2<k< 或 <k<5时,方程 表示椭圆.
答案:
2.2.1 椭圆及其标准方程1.椭圆的定义
(1)定义:平面内与两个定点F1,F2的距离之和等于_____(大于
|F1F2|)的点的轨迹.
(2)焦点:两个定点F1,F2.
(3)焦距:两焦点间的距离|F1F2|.
(4)几何表示:|MF1|+|MF2|=___(常数)且2a__|F1F2|.常数2a>2.椭圆的标准方程(-c,0),(c,0)(0,-c),(0,c)a2=b2+c21.判一判(正确的打“√”,错误的打“×”)
(1)椭圆的两种标准方程中,虽然焦点位置不同,但都有a2=b2+c2.( )
(2)平面内到两个定点F1,F2的距离之和等于常数的点的集合是椭圆.( )
(3)椭圆的特殊形式是圆.( )【解析】(1)正确.无论在哪种标准方程中,一定都有a2=b2+c2.
(2)错误.只有常数大于|F1F2|时,点的集合才是椭圆.
(3)错误.椭圆与圆的概念不同,没有特殊情况.
答案:(1)√ (2)× (3)×2.做一做(请把正确的答案写在横线上)
(1)a=5,c=3,焦点在x轴上的椭圆标准方程为 .
(2)方程4x2+9y2=1的焦点坐标为 .
(3)椭圆的方程为 则a= ,b= ,
c= .【解析】(1)由a2=b2+c2,得b2=52-32=42=16,
所以椭圆的方程为
答案:
(2)由4x2+9y2=1,得 所以
所以焦点坐标为
答案:(3)由 所以a2=9,b2=4,c2=5.
所以a=3,b=2,c=
答案:3 2【要点探究】
知识点 1 椭圆的定义
1.对椭圆定义的三点说明
(1)椭圆是在平面内定义的,所以“平面内”这一条件不能视.
(2)定义中到两定点的距离之和是常数,而不能是变量.
(3)常数(2a)必须大于两定点间的距离,否则轨迹不是椭圆,这是判断一曲线是否为椭圆的限制条件.2.椭圆定义的两个应用
(1)若|MF1|+|MF2|=2a(2a>|F1F2|),则动点M的轨迹是椭圆.
(2)若点M在椭圆上,则|MF1|+|MF2|=2a.【知识拓展】椭圆的焦点三角形
设M为椭圆 上任意一点
(不在x轴上).F1,F2为焦点,则
△MF1F2为椭圆的焦点三角形.【微思考】
在椭圆的定义中,动点M到两定点F1,F2的距离之和等于常数(2a)且2a>|F1F2|,若2a=|F1F2|,则M的轨迹是什么?若2a<|F1F2|,则M的轨迹是什么?
提示:当2a=|F1F2|时,点M的轨迹是线段F1F2;
当2a<|F1F2|时,点M的轨迹不存在.【即时练】
1.椭圆 的左、右焦点分别为F1,F2,点P在椭圆上,
若|PF1|=4,则|PF2|=________.
2.已知椭圆 的两焦点为F1,F2,弦AB过点F1,则
△ABF2的周长为_________.【解析】1.由椭圆的定义知|PF1|+|PF2|=6,
所以|PF2|=6-|PF1|=6-4=2.
答案:2
2.由椭圆的定义知2a=10,
△ABF2的周长为|AB|+|AF2|+|BF2|
=|AF1|+|AF2|+|BF1|+|BF2|=4a=20.
答案:20知识点 2 椭圆的标准方程
对椭圆标准方程的三点认识
(1)标准方程的几何特征:椭圆的中心在坐标原点,焦点在x轴或
y轴上.
(2)标准方程的代数特征:方程右边为1,左边是关于 的
平方和,并且分母为不相等的正值.(3)a,b,c三个量的关系:椭圆的标准方程中,
a表示椭圆上的点M到两焦点间距离的和的一
半,可借助图形帮助记忆.a,b,c(都是正数)
恰是构成一个直角三角形的三条边,a是斜边,所以a>b,a>c,且a2=b2+c2.(如图所示)【微思考】
(1)在椭圆的标准方程中a>b>c一定成立吗?
提示:不一定,只要a>b,a>c即可,b,c大小关系不定.
(2)根据椭圆方程,如何确定焦点位置?
提示:把方程化为标准形式,x2,y2的分母哪个大,焦点就在相应的轴上.【即时练】
椭圆25x2+16y2=400的焦点坐标为 ,焦距为_______.
【解析】把方程化为标准式:
可知焦点在y轴上,
则a2=25,b2=16,所以c2=25-16=9,
则c=3,所以焦点为(0,±3),焦距为2c=6.
答案:(0,±3) 6 【题型示范】
类型一 求椭圆的标准方程
【典例1】
(1)过点(-3,2)且与 有相同
焦点的椭圆的方程是( )(2)求适合下列条件的椭圆的标准方程:
①两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0).
②焦点在y轴上,且经过两个点(0,2)和(1,0).
③经过点 和点【解题探究】1.题(1)焦点在哪个轴上?
2.题①焦点在x轴上的椭圆的标准方程是怎样的?
题②焦点在y轴上的椭圆的标准方程是怎样的?
题③焦点位置不确定,椭圆的标准方程应如何求?【探究提示】1.椭圆的焦点在x轴上,因为已知方程中x2项的分母较大.
2.① (a>b>0);
② (a>b>0);
③应分焦点在x轴上,y轴上两种情况讨论求解.【自主解答】(1)选A.由方程 可知,其焦点的坐标为
即
设所求椭圆方程为 (a>b>0).
因为过点(-3,2),代入方程为 解得a2=15(a2=3舍去).
故方程为(2)①由于椭圆的焦点在x轴上,
所以设它的标准方程为 (a>b>0).
因为 所以a=5.
又c=4,所以b2=a2-c2=25-16=9.
故所求椭圆的标准方程为②由于椭圆的焦点在y轴上,
所以设它的标准方程为 (a>b>0).
由于椭圆经过点(0,2)和(1,0),
所以
故所求椭圆的标准方程为③方法一:当焦点在x轴上时,
设椭圆的标准方程为 (a>b>0).
依题意有 解得
故所求椭圆的标准方程为当焦点在y轴上时,设椭圆的标准方程为 (a>b>0).
依题意有 解得
因为a>b>0,所以无解.
综上,所求椭圆的标准方程为方法二:设所求椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n),
依题意有 解得
所以所求的椭圆方程为:【方法技巧】
1.求椭圆方程的方法2.椭圆方程的设法技巧
若椭圆的焦点位置不确定,需要分焦点在x轴上和在y轴上两种情况讨论,也可设椭圆的方程为mx2+ny2=1(m>0,n>0,m≠n).【变式训练】求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是(-2,0),(2,0),椭圆上一点P到两焦点距离之和等于6,求椭圆的方程.
(2)椭圆的焦点为F1(0,-5),F2(0,5),点P(3,4)是椭圆上的一个点,求椭圆的方程.【解析】(1)由椭圆的焦点坐标为(-2,0),(2,0),
所以可设椭圆的方程为: (a>b>0).
因为2a=6,2c=4,所以a=3,c=2,
所以b2=a2-c2=5,
所以所求点的轨迹方程为:(2)因为焦点为F1(0,-5),F2(0,5),可设椭圆方程为
2a=
所以a= c=5,b2=40-25=15,
所以椭圆方程为【补偿训练】已知椭圆 (a>b>0)上一点P(3,4),
且两焦点分别为F1,F2,若PF1⊥PF2,试求椭圆方程.
【解题指南】由PF1⊥PF2,可得出 求出c的值.再
根据点P在椭圆上,且a2=b2+c2,建立a,b的方程组,求出a,b的
值.【解析】因为椭圆经过点P(3,4),
所以
又a2=b2+c2, ②
设F1(-c,0),F2(c,0),
则
因为PF1⊥PF2,
所以所以
即9-c2=-16.
所以c2=25.所以c=5.
由①②可得
所以a2=45,b2=20.
故所求椭圆方程为类型二 与椭圆有关的轨迹问题
【典例2】
(1)已知点M在椭圆 上,MP′垂直于椭圆焦点所在的
直线,垂足为P′,并且M为线段PP′的中点,则P点的轨迹方
程为________.
(2)(2013·新课标全国卷Ⅰ改编)已知圆M:(x+1)2+y2=1,圆
N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹
为曲线C.求C的方程.【解题探究】1.题(1)动点P与哪个动点有关?本题可采用什么方法求动点P的轨迹方程?
2.两圆外切时能得到什么条件?内切时能得到什么条件?
【探究提示】1.动点P与点M有关.因为点M在已知椭圆上运动,所以本题可采用代入法求动点P的轨迹方程.
2.两圆外切,两圆的圆心距等于半径之和;两圆内切,两圆的圆心距等于半径差的绝对值.【自主解答】(1)设点P的坐标为(x,y),M点的坐标为(x0,y0).
因为点M在椭圆 上,所以
因为M是线段PP′的中点,所以
把 代入 得
即x2+y2=36.
所以点P的轨迹方程为x2+y2=36.
答案:x2+y2=36(2)由已知得圆M的圆心为M(-1,0),半径r1=1;圆N的圆心为
N(1,0),半径r2=3.设圆P的圆心为P(x,y),半径为R.动圆P与圆
M外切并且与圆N内切,
所以|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4.
由椭圆定义可知,曲线C是以M,N为左、右焦点,长半轴长为
2,短半轴长为 的椭圆(左顶点除外),其方程为
(x≠-2).【方法技巧】求解与椭圆相关的轨迹问题的方法【变式训练】已知两定点F1(-1,0),F2(1,0),且|F1F2|是|PF1|与|PF2|的等差中项,则动点P的轨迹方程是( )【解析】选C.因为|F1F2|是|PF1|和|PF2|的等差中项,
所以|PF1|+|PF2|=2|F1F2|=2×2=4>|F1F2|.
所以P的轨迹应是以F1,F2为焦点的椭圆.
这里c=1,a=2.
所以轨迹方程为【补偿训练】求过点P(3,0)且与圆x2+6x+y2-91=0相内切的动
圆圆心的轨迹方程.
【解析】圆方程配方整理得(x+3)2+y2=102,圆心为C1(-3,0),半
径为R=10.设所求动圆圆心为C(x,y),半径为r,依题意有
消去r得R-|PC|=|CC1|?|PC|+
|CC1|=R,即|PC|+|CC1|=10.又P(3,0),C1(-3,0),且|PC1|=6<10.可见C点是以P,C1为两焦点的椭圆,且c=3,2a=10,
所以a=5,从而b=4,
故所求的动圆圆心的轨迹方程为类型三 求参数的取值范围
【典例3】
(1)已知方程 表示焦点在y轴上的椭圆,则m的
取值范围为__________.
(2) 已知x2sin α+y2cos α=1(0≤α≤π)表示焦点在x轴上的椭圆.求α的取值范围.【解题探究】1.题(1)已知椭圆标准方程为 其中m,n
应满足什么条件?
2.题(2)如何将x2sin α+y2cos α=1化成标准形式?【探究提示】1.m,n应满足条件 若焦点在x轴上,应有
m>n;若焦点在y轴上,应有m<n.
2.当sin α≠0,cos α≠0时,方程x2sin α+y2cos α=1可
化为【自主解答】(1)由题意得: 即
所以
答案:(2)由题意可将已知方程化为
因为椭圆的焦点在x轴上,
所以 即
又因为0≤α≤π,所以
即所求α的取值范围是【延伸探究】若把题(1)中方程改为 其余条件
不变,求m的取值范围.
【解析】由题意得
①当m>0时,
所以②当m<0时, 所以m<-1.
所以m的取值范围是【方法技巧】求参数取值范围的方法
(1)求参数的范围就是根据条件列出参数为未知量的不等式(组)或方程(组),把问题转化为不等式(组)或方程(组)的求解问题.
(2)对于椭圆,如果焦点所在的位置不确定,就需分两种情况分别列式求解. 【变式训练】椭圆5x2+ky2=5的一个焦点是(0,2),那么实数k的值为( )
A.-25 B.25 C.-1 D.1
【解析】选D.由5x2+ky2=5,得 因为一个焦点是
(0,2),所以 得k=1.【补偿训练】如果方程 表示焦点在x轴上的椭圆,
则实数a的取值范围是( )
A.a>3 B.a<-2
C.a<-2或a>3 D.-6<a<-2或a>3
【解析】选D.因为方程 表示焦点在x轴上的椭圆,
所以有
解得a>3或-6<a<-2.【易错误区】对椭圆标准方程理解不清致误
【典例】若方程 表示椭圆,则m满足的条件是
_______.
【解析】由方程 表示椭圆,
知 解得 且m≠1.
答案:【常见误区】【防范措施】
牢记标准方程的特点
必须明确形如方程 表示椭圆、圆的条件,如本例中,
方程表示椭圆.首先应满足A≠B,其次应有A>0,B>0,事实上,当
A=B时,方程表示的曲线为圆而非椭圆.【类题试解】若方程 表
示椭圆,则实数k的取值范围是________.
【解析】由方程 表示椭圆,可得
解得2<k<5且
即当2<k< 或 <k<5时,方程 表示椭圆.
答案:
