2.2.2 椭圆的简单几何性质 课件2
文档属性
| 名称 | 2.2.2 椭圆的简单几何性质 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 17:16:57 | ||
图片预览





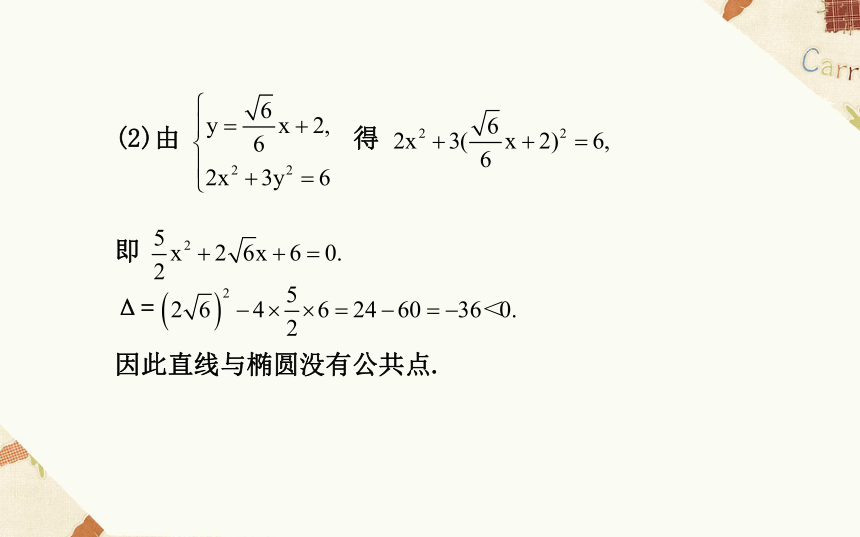




文档简介
课件68张PPT。2.2.2
椭圆方程及性质的应用 【题型示范】
类型一 直线与椭圆的位置关系
【典例1】
(1)若直线y=kx+1与焦点在x轴上的椭圆 总有公共
点,则m的取值范围为________.
(2)判断直线l: 和椭圆2x2+3y2=6是否有公共点.【解题探究】1.题(1)中直线y=kx+1是否恒过定点?若恒过定点,过哪个定点?当点在什么位置时,经过该点的直线总与椭圆有公共点?
2.题(2)判断直线是否与椭圆有公共点,常用什么方法?
【探究提示】1.恒过定点(0,1),当点在椭圆上或在椭圆内部时,经过该点的直线与椭圆总有公共点.
2.判断直线与椭圆是否有公共点,往往利用判别式的符号进行判断.【自主解答】(1)方法一:由 消去y,整理得
(m+5k2)x2+10kx+5(1-m)=0,
所以Δ=100k2-20(m+5k2)(1-m)=20m(5k2+m-1).
因为直线与椭圆总有公共点,
所以Δ≥0对任意k∈R都成立.
因为m>0,所以5k2≥1-m恒成立,所以1-m≤0,即m≥1.
又因为椭圆的焦点在x轴上,所以0所以1≤m<5.方法二:因为直线y=kx+1过定点M(0,1),
所以要使直线与该椭圆总有公共点,则点M(0,1)必在椭圆内或
椭圆上,由此得 解得1≤m<5.
答案:[1,5)(2)由 得
即
Δ=
因此直线与椭圆没有公共点.【延伸探究】题(2)条件不变,问椭圆上是否存在一点,它到
直线l的距离最大?最大距离是多少?
【解析】因为直线l与椭圆2x2+3y2=6不相交,设与椭圆相切的
直线m平行于直线l,则直线m的方程为:
由方程组 消去y得:
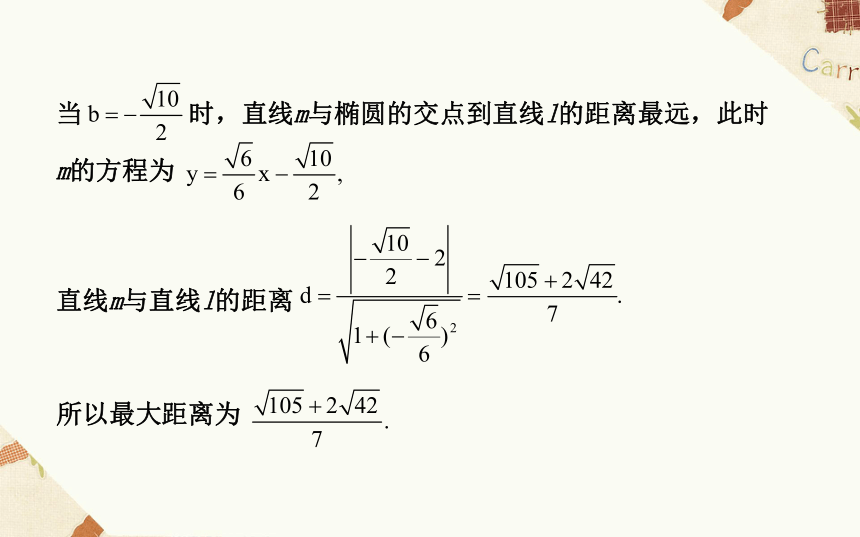
即 由Δ=0,得 或当 时,直线m与椭圆的交点到直线l的距离最远,此时
m的方程为
直线m与直线l的距离
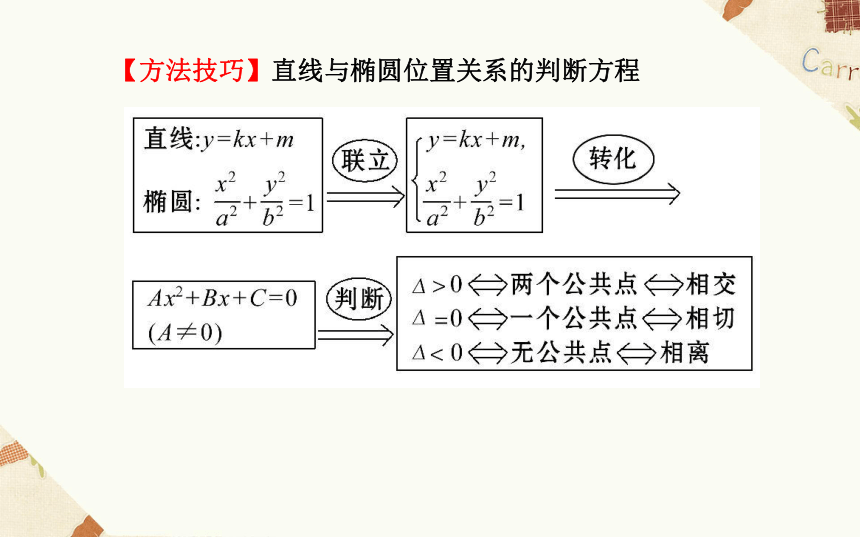
所以最大距离为【方法技巧】直线与椭圆位置关系的判断方程【变式训练】已知椭圆C: 一个顶点为A(0,2).
(1)若将椭圆C绕点P(1,2)旋转180°得到椭圆D,求椭圆D的方程.
(2)若椭圆C与直线y=kx+m(k≠0)相交于不同的M,N两点,且
|AM|=|AN|,求m的取值范围.【解析】(1)由题意得,椭圆C的对称中心(0,0)关于点P(1,2)
的对称点为(2,4),且对称轴平行于坐标轴,长轴、短轴的长
度不变,故将椭圆C绕点P(1,2)旋转180°得到椭圆D的方程为(2)设M(x1,y1),N(x2,y2).
所以|AM|=|AN|,所以A在线段MN的垂直平分线上,
把M(x1,y1),N(x2,y2)分别代入椭圆C: 得:用①减去②得:
所以 再由垂直平分线的性质得
所以
所以y1+y2=-2,所以x1+x2=-3k(y1+y2)=6k,
故MN的中点(3k,-1),把y=kx+m代入椭圆C: 得,
(1+3k2)x2+6kmx+3m2-12=0,
所以x1+x2=6k=
所以m=-(1+3k2),所以-mx2+6kmx+3m2-12=0,
由题意知,判别式大于0,即36k2m2+4m(3m2-12)>0,
m(m-4)<0,所以0线 有且仅有一个交点,求椭圆的长轴长.
【解析】设椭圆长轴长为2a(且a>2),
则椭圆方程为
由 得因为直线与椭圆只有一个交点,所以Δ=0,即192(a2-4)2-
16(a2-3)×(16-a2)×(a2-4)=0,解得a=0(舍去),a=2(舍去),
所以长轴长类型二 弦长及中点弦问题
【典例2】
(1)椭圆4x2+9y2=144内一点P(3,2),过点P的弦恰好以P为中点,那么这弦所在的直线方程为( )
A.3x+2y-12=0 B.2x+3y-12=0
C.4x+9y-144=0 D.9x+4y-144=0(2)已知椭圆C的对称轴为坐标轴,且短轴长为4,离心率为
①求椭圆C的方程;
②设椭圆C的焦点在y轴上,斜率为1的直线l与C相交于A,B两
点,且 求直线l的方程.【解题探究】1.题(1)求弦所在直线的方程,还需确定什么?
如何利用中点这个条件?
2.题(2)求弦长的一般思路是什么?你能得出弦长的公式吗?
【探究提示】1.还需确定直线的斜率,可设出弦的两个端点坐
标,利用中点坐标公式,找它们之间的联系.
2.一般思路是联立直线与椭圆的方程,消元得到关于x(或y)的
一元二次方程,由根与系数的关系得
故弦长为【自主解答】(1)选B.设弦的两个端点分别为P1(x1,y1),
P2(x2,y2),弦所在直线的斜率为k,则 ①,
②.
①-②得:4(x1-x2)(x1+x2)+9(y1-y2)(y1+y2)=0,
又
因此可得:4(x1-x2)×6+9(y1-y2)×4=0,
所以
故弦所在直线方程为
即2x+3y-12=0,选B.(2)①设椭圆C的长半轴长为a(a>0),短半轴长为b(b>0),
则2b=4,由
解得a=4,b=2.
因为椭圆C的对称轴为坐标轴,
所以椭圆C的方程为 或②设直线l的方程为y=x+m,A(x1,y1),B(x2,y2),
由方程组
消去y,得5x2+2mx+m2-16=0,
由题意,得Δ=(2m)2-20(m2-16)>0,
且
因为|AB|=
=所以
解得m=±2,
验证知Δ>0成立,
所以直线l的方程为x-y+2=0或x-y-2=0.【方法技巧】
1.直线与椭圆相交弦的弦长问题
直线与椭圆相交有关弦的问题,主要思路是联立直线和椭圆的方程,得到一元二次方程,然后借助一元二次方程的有关知识解决,有时运用弦长公式,解题时应注意以下几点:
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.
(2)当弦的两端点的坐标不易求时,可用弦长公式.
(3)如果直线方程涉及斜率,要注意斜率不存在的情况.2.解决椭圆中点弦问题的三种方法
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.(2)点差法:利用端点在曲线上,坐标满足方程,将端点坐标
分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关
系,具体如下: 已知A(x1,y1),B(x2,y2)是椭圆
(a>b>0)上的两个不同的点,M(x0,y0)是线段AB的中点,则由①-②,得 变形得
即
(3)共线法:利用中点坐标公式,如果弦的中点为P(x0,y0),
设其一交点为A(x,y),则另一交点为B(2x0-x,2y0-y),
则
两式作差即得所求直线方程.【变式训练】直线y=x+1被椭圆 所截得的弦的中点
坐标是( )
【解析】选C.由 消去y,得3x2+4x-2=0,设弦的两端点坐标为(x1,y1),(x2,y2),
中点坐标为(x中,y中),
则x1+x2= 所以x中=
从而y中=x中+1=
所以中点坐标为【补偿训练】椭圆x2+4y2=16被直线 截得的弦长为
____________.
【解析】由 消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
所以弦长
=
答案:类型三 与椭圆有关的综合问题
【典例3】
(1)椭圆 (a>b>0)与直线x+y=1交于P,Q两点,且
OP⊥OQ,其中O为坐标原点,则 =_______.(2)已知椭圆 (a>b>0)的离心率为 短轴的一个端点到右焦点的距离为 直线l:y=kx+m交椭圆于不同的两点A,B.
①求椭圆的方程;
②若坐标原点O到直线l的距离为 求△AOB面积的最大值.【解题探究】1.题(1)中一般将条件OP⊥OQ转化为什么?
2.题(2)中求△AOB面积的最大值,关键是求什么?
【探究提示】1.条件OP⊥OQ,一般转化为向量 . =0来处
理.
2.关键是求|AB|的最大值.OPOQ【自主解答】(1)设P(x1,y1),Q(x2,y2),
由OP⊥OQ? ?x1x2+y1y2=0.
因为y1=1-x1,y2=1-x2,代入上式得:
2x1x2-(x1+x2)+1=0 (*)
又将y=1-x代入 ?(a2+b2)x2-2a2x+a2(1-b2)=0,因为
Δ>0,所以x1+x2= x1x2= 代入(*)化简得
答案:2(2)①由 所以 b=1,
所以椭圆的方程为:
②由已知 所以
联立l:y=kx+m和
消去y,整理可得:
(1+3k2)x2+6kmx+3m2-3=0,
所以Δ=(6km)2-4(1+3k2)(3m2-3)>0,设A(x1,y1),B(x2,y2),
则
所以|AB|2=(1+k2)(x1-x2)2=
=
= (k≠0),当且仅当 时取等号,
验证知 满足题意,
显然k=0时,|AB|2=3<4.
所以(S△AOB)max=【方法技巧】解椭圆综合问题的常用技巧
椭圆是圆锥曲线中重要的一种曲线,它可以同其他章节知识结合考查,如不等式、三角函数以及平面向量等.解决这类问题时要注意方程思想、函数思想及转化的思想,其中利用方程中根与系数的关系构造方程或函数是常用的技巧.【变式训练】设F1,F2分别是椭圆E: (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|.
(1)若|AB|=4,△ABF2的周长为16,求|AF2|.
(2)若cos∠AF2B= ,求椭圆E的离心率.【解题指南】(1)利用椭圆的定义求解.
(2)设|BF1|=k,用a,k表示|AF2|,|BF2|,利用余弦定理解△ABF2得出等腰Rt△AF1F2,从而得到a,c的关系式.【解析】(1)由|AF1|=3|BF1|,|AB|=4,
得|AF1|=3,|BF1|=1,
因为△ABF2的周长为16,
所以由椭圆定义可得4a=16,|AF1|+|AF2|=2a=8,
故|AF2|=2a-|AF1|=8-3=5.(2)设|BF1|=k,则k>0,且|AF1|=3k,|AB|=4k,
由椭圆定义可得|AF2|=2a-3k,|BF2|=2a-k,
在△ABF2中,由余弦定理可得
|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2|cos∠AF2B,
即(4k)2=(2a-3k)2+(2a-k)2- (2a-3k)(2a-k),
化简可得(a+k)(a-3k)=0,而a+k>0,
故a=3k,于是有|AF2|=3k=|AF1|,|BF2|=5k,因此|BF2|2=|AF2|2+|AB|2?F1A⊥F2A,
故△AF1F2为等腰直角三角形,
从而c= 【补偿训练】已知椭圆G: (a>b>0)的离心率为
右焦点为 斜率为1的直线l与椭圆G交于A,B两点,以
AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程.
(2)求△PAB的面积.【解析】(1)由已知得
解得 又b2=a2-c2=4,
所以椭圆G的方程为
(2)设直线l的方程为y=x+m,
由 得4x2+6mx+3m2-12=0 ①设A,B的坐标分别为(x1,y1),(x2,y2)(x1<x2),
AB的中点为E(x0,y0),
则
因为AB是等腰△PAB的底边,所以PE⊥AB.
所以PE的斜率 解得m=2.
此时方程①为4x2+12x=0,
解得x1=-3,x2=0,所以y1=-1,y2=2.所以
此时,点P(-3,2)到直线AB:x-y+2=0的距离
所以△PAB的面积【拓展类型】椭圆中的最值问题
【备选例题】(1)斜率为1的直线l与椭圆 相交于A,B
两点,则|AB|的最大值为_________.
(2)如图,动圆C1:x2+y2=t2,1A,B,C,D四点,点A1,A2分别为C2的左、右顶点.①当t为何值时,矩形ABCD的面积取得最大值?并求出其最大面积;
②求直线AA1与直线A2B交点M的轨迹方程.【解析】(1)方法一:设直线l的方程为y=x+t,
由 消去y得
整理,得5x2+8tx+4(t2-1)=0.
因为Δ=64t2-80(t2-1)>0,所以设直线与椭圆交于A(x1,y1),B(x2,y2)两点,
则
所以|AB|=
=
当t=0时,|AB|为最大,即|AB|max=方法二:根据椭圆的对称性,当直线斜率固定时,直线过原点
时截椭圆所得弦长最长,将y=x代入 得交点坐标为
和 故
答案:(2)①设A(x0,y0)(-3由 得
从而
当 时,Smax=6.
从而t= 时,矩形ABCD的面积最大,最大面积为6.②由A(x0,y0),B(x0,-y0),A1(-3,0),A2(3,0)知直线AA1的方程为
①
直线A2B的方程为 ②
由①②得 ③
又点A(x0,y0)在椭圆C上,故 ④
将④代入③得 (x<-3,y<0).
因此点M的轨迹方程为 (x<-3,y<0).【方法技巧】解决与椭圆有关的最值问题的三种方法
(1)定义法:利用定义转化为几何问题处理.
(2)数形结合法:利用数与形的结合,挖掘几何特征,进而求解.
(3)函数法:探求函数模型,转化为函数的最值问题来处理,注意椭圆的范围. 【规范解答】椭圆与平面向量的综合问题
【典例】(12分)设椭圆 (a>b>0)
的左焦点为F,离心率为 过点F且与x轴垂直的直线被椭圆
截得的线段长为
(1)求椭圆的方程.
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与
椭圆交于C,D两点.若 AC·DB+AD·CB=8 求k的值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时,若求不出直线与椭圆交点的纵坐标,即得不出①处,则会导致求不出椭圆方程而本例不得分.
失分点2:若在②处化简整理结果时错误,则会导致下面运算全部错误,本例最多能得6分.
失分点3:若在③处向量的运算不能转化为坐标间关系,则得不出关于k的等量关系而失3~4分.【悟题】提措施,导方向
1.加强运算能力的培养
椭圆的综合问题,一般涉及的运算量较大,因此在平时学习中,要多注重运算能力的培养,防止因运算错误而失分,如本例(1)(2)问求解时,都涉及较大的运算量.2.向量关系的应用
在解析几何中,向量的运算常通过坐标的运算来实现,对向量
相等、向量的数量积、共线向量的坐标表示要熟练掌握,如本
例 是建立关于k的方程的关键.【类题试解】在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴上,短轴长为2,离心率为
(1)求椭圆C的方程.
(2)A,B为椭圆C上满足△AOB的面积为 的任意两点,E为线
段AB的中点,射线OE交椭圆C于点P,设 ,求实数t的值.【解析】(1)设椭圆C的方程为 (a>b>0),
由题意知 解得 因此椭圆C的方程为(2)当AB⊥x轴时,设A(x0,y0),B(x0,-y0),
由 得 或
由 =t(x0,0)=(tx0,0),得P(tx0,0),
又P在椭圆上,所以 所以 或
所以t=2或 (舍去负值).当AB不垂直于x轴时,设AB:y=kx+m,显然m≠0,代入椭圆方
程得(1+2k2)x2+4kmx+2(m2-1)=0. (*)
由三角形面积公式知, |xAyB-xByA|= |xA(kxB+m)-
xB(kxA+m)|= |m||xA-xB|=
所以,|xA-xB|= ?(xA+xB)2-4xAxB=
即整理得, ①
又 所以,
即
将其代入椭圆方程得 整理可得,
1+2k2=m2t2, ②联立①②,消去1+2k2,约分掉m2,移项整理得,3t4-16t2+16=0,
解之可得,t2=4或 均能使(*)式的Δ>0,所以t=2或 (舍去负值).
综上,t=2或
椭圆方程及性质的应用 【题型示范】
类型一 直线与椭圆的位置关系
【典例1】
(1)若直线y=kx+1与焦点在x轴上的椭圆 总有公共
点,则m的取值范围为________.
(2)判断直线l: 和椭圆2x2+3y2=6是否有公共点.【解题探究】1.题(1)中直线y=kx+1是否恒过定点?若恒过定点,过哪个定点?当点在什么位置时,经过该点的直线总与椭圆有公共点?
2.题(2)判断直线是否与椭圆有公共点,常用什么方法?
【探究提示】1.恒过定点(0,1),当点在椭圆上或在椭圆内部时,经过该点的直线与椭圆总有公共点.
2.判断直线与椭圆是否有公共点,往往利用判别式的符号进行判断.【自主解答】(1)方法一:由 消去y,整理得
(m+5k2)x2+10kx+5(1-m)=0,
所以Δ=100k2-20(m+5k2)(1-m)=20m(5k2+m-1).
因为直线与椭圆总有公共点,
所以Δ≥0对任意k∈R都成立.
因为m>0,所以5k2≥1-m恒成立,所以1-m≤0,即m≥1.
又因为椭圆的焦点在x轴上,所以0
所以要使直线与该椭圆总有公共点,则点M(0,1)必在椭圆内或
椭圆上,由此得 解得1≤m<5.
答案:[1,5)(2)由 得
即
Δ=
因此直线与椭圆没有公共点.【延伸探究】题(2)条件不变,问椭圆上是否存在一点,它到
直线l的距离最大?最大距离是多少?
【解析】因为直线l与椭圆2x2+3y2=6不相交,设与椭圆相切的
直线m平行于直线l,则直线m的方程为:
由方程组 消去y得:
即 由Δ=0,得 或当 时,直线m与椭圆的交点到直线l的距离最远,此时
m的方程为
直线m与直线l的距离
所以最大距离为【方法技巧】直线与椭圆位置关系的判断方程【变式训练】已知椭圆C: 一个顶点为A(0,2).
(1)若将椭圆C绕点P(1,2)旋转180°得到椭圆D,求椭圆D的方程.
(2)若椭圆C与直线y=kx+m(k≠0)相交于不同的M,N两点,且
|AM|=|AN|,求m的取值范围.【解析】(1)由题意得,椭圆C的对称中心(0,0)关于点P(1,2)
的对称点为(2,4),且对称轴平行于坐标轴,长轴、短轴的长
度不变,故将椭圆C绕点P(1,2)旋转180°得到椭圆D的方程为(2)设M(x1,y1),N(x2,y2).
所以|AM|=|AN|,所以A在线段MN的垂直平分线上,
把M(x1,y1),N(x2,y2)分别代入椭圆C: 得:用①减去②得:
所以 再由垂直平分线的性质得
所以
所以y1+y2=-2,所以x1+x2=-3k(y1+y2)=6k,
故MN的中点(3k,-1),把y=kx+m代入椭圆C: 得,
(1+3k2)x2+6kmx+3m2-12=0,
所以x1+x2=6k=
所以m=-(1+3k2),所以-mx2+6kmx+3m2-12=0,
由题意知,判别式大于0,即36k2m2+4m(3m2-12)>0,
m(m-4)<0,所以0
【解析】设椭圆长轴长为2a(且a>2),
则椭圆方程为
由 得因为直线与椭圆只有一个交点,所以Δ=0,即192(a2-4)2-
16(a2-3)×(16-a2)×(a2-4)=0,解得a=0(舍去),a=2(舍去),
所以长轴长类型二 弦长及中点弦问题
【典例2】
(1)椭圆4x2+9y2=144内一点P(3,2),过点P的弦恰好以P为中点,那么这弦所在的直线方程为( )
A.3x+2y-12=0 B.2x+3y-12=0
C.4x+9y-144=0 D.9x+4y-144=0(2)已知椭圆C的对称轴为坐标轴,且短轴长为4,离心率为
①求椭圆C的方程;
②设椭圆C的焦点在y轴上,斜率为1的直线l与C相交于A,B两
点,且 求直线l的方程.【解题探究】1.题(1)求弦所在直线的方程,还需确定什么?
如何利用中点这个条件?
2.题(2)求弦长的一般思路是什么?你能得出弦长的公式吗?
【探究提示】1.还需确定直线的斜率,可设出弦的两个端点坐
标,利用中点坐标公式,找它们之间的联系.
2.一般思路是联立直线与椭圆的方程,消元得到关于x(或y)的
一元二次方程,由根与系数的关系得
故弦长为【自主解答】(1)选B.设弦的两个端点分别为P1(x1,y1),
P2(x2,y2),弦所在直线的斜率为k,则 ①,
②.
①-②得:4(x1-x2)(x1+x2)+9(y1-y2)(y1+y2)=0,
又
因此可得:4(x1-x2)×6+9(y1-y2)×4=0,
所以
故弦所在直线方程为
即2x+3y-12=0,选B.(2)①设椭圆C的长半轴长为a(a>0),短半轴长为b(b>0),
则2b=4,由
解得a=4,b=2.
因为椭圆C的对称轴为坐标轴,
所以椭圆C的方程为 或②设直线l的方程为y=x+m,A(x1,y1),B(x2,y2),
由方程组
消去y,得5x2+2mx+m2-16=0,
由题意,得Δ=(2m)2-20(m2-16)>0,
且
因为|AB|=
=所以
解得m=±2,
验证知Δ>0成立,
所以直线l的方程为x-y+2=0或x-y-2=0.【方法技巧】
1.直线与椭圆相交弦的弦长问题
直线与椭圆相交有关弦的问题,主要思路是联立直线和椭圆的方程,得到一元二次方程,然后借助一元二次方程的有关知识解决,有时运用弦长公式,解题时应注意以下几点:
(1)当弦的两端点的坐标易求时,可直接求出交点坐标,再用两点间距离公式求弦长.
(2)当弦的两端点的坐标不易求时,可用弦长公式.
(3)如果直线方程涉及斜率,要注意斜率不存在的情况.2.解决椭圆中点弦问题的三种方法
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.(2)点差法:利用端点在曲线上,坐标满足方程,将端点坐标
分别代入椭圆方程,然后作差,构造出中点坐标和斜率的关
系,具体如下: 已知A(x1,y1),B(x2,y2)是椭圆
(a>b>0)上的两个不同的点,M(x0,y0)是线段AB的中点,则由①-②,得 变形得
即
(3)共线法:利用中点坐标公式,如果弦的中点为P(x0,y0),
设其一交点为A(x,y),则另一交点为B(2x0-x,2y0-y),
则
两式作差即得所求直线方程.【变式训练】直线y=x+1被椭圆 所截得的弦的中点
坐标是( )
【解析】选C.由 消去y,得3x2+4x-2=0,设弦的两端点坐标为(x1,y1),(x2,y2),
中点坐标为(x中,y中),
则x1+x2= 所以x中=
从而y中=x中+1=
所以中点坐标为【补偿训练】椭圆x2+4y2=16被直线 截得的弦长为
____________.
【解析】由 消去y并化简得x2+2x-6=0.
设直线与椭圆的交点为M(x1,y1),N(x2,y2),
则x1+x2=-2,x1x2=-6.
所以弦长
=
答案:类型三 与椭圆有关的综合问题
【典例3】
(1)椭圆 (a>b>0)与直线x+y=1交于P,Q两点,且
OP⊥OQ,其中O为坐标原点,则 =_______.(2)已知椭圆 (a>b>0)的离心率为 短轴的一个端点到右焦点的距离为 直线l:y=kx+m交椭圆于不同的两点A,B.
①求椭圆的方程;
②若坐标原点O到直线l的距离为 求△AOB面积的最大值.【解题探究】1.题(1)中一般将条件OP⊥OQ转化为什么?
2.题(2)中求△AOB面积的最大值,关键是求什么?
【探究提示】1.条件OP⊥OQ,一般转化为向量 . =0来处
理.
2.关键是求|AB|的最大值.OPOQ【自主解答】(1)设P(x1,y1),Q(x2,y2),
由OP⊥OQ? ?x1x2+y1y2=0.
因为y1=1-x1,y2=1-x2,代入上式得:
2x1x2-(x1+x2)+1=0 (*)
又将y=1-x代入 ?(a2+b2)x2-2a2x+a2(1-b2)=0,因为
Δ>0,所以x1+x2= x1x2= 代入(*)化简得
答案:2(2)①由 所以 b=1,
所以椭圆的方程为:
②由已知 所以
联立l:y=kx+m和
消去y,整理可得:
(1+3k2)x2+6kmx+3m2-3=0,
所以Δ=(6km)2-4(1+3k2)(3m2-3)>0,设A(x1,y1),B(x2,y2),
则
所以|AB|2=(1+k2)(x1-x2)2=
=
= (k≠0),当且仅当 时取等号,
验证知 满足题意,
显然k=0时,|AB|2=3<4.
所以(S△AOB)max=【方法技巧】解椭圆综合问题的常用技巧
椭圆是圆锥曲线中重要的一种曲线,它可以同其他章节知识结合考查,如不等式、三角函数以及平面向量等.解决这类问题时要注意方程思想、函数思想及转化的思想,其中利用方程中根与系数的关系构造方程或函数是常用的技巧.【变式训练】设F1,F2分别是椭圆E: (a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|BF1|.
(1)若|AB|=4,△ABF2的周长为16,求|AF2|.
(2)若cos∠AF2B= ,求椭圆E的离心率.【解题指南】(1)利用椭圆的定义求解.
(2)设|BF1|=k,用a,k表示|AF2|,|BF2|,利用余弦定理解△ABF2得出等腰Rt△AF1F2,从而得到a,c的关系式.【解析】(1)由|AF1|=3|BF1|,|AB|=4,
得|AF1|=3,|BF1|=1,
因为△ABF2的周长为16,
所以由椭圆定义可得4a=16,|AF1|+|AF2|=2a=8,
故|AF2|=2a-|AF1|=8-3=5.(2)设|BF1|=k,则k>0,且|AF1|=3k,|AB|=4k,
由椭圆定义可得|AF2|=2a-3k,|BF2|=2a-k,
在△ABF2中,由余弦定理可得
|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2|cos∠AF2B,
即(4k)2=(2a-3k)2+(2a-k)2- (2a-3k)(2a-k),
化简可得(a+k)(a-3k)=0,而a+k>0,
故a=3k,于是有|AF2|=3k=|AF1|,|BF2|=5k,因此|BF2|2=|AF2|2+|AB|2?F1A⊥F2A,
故△AF1F2为等腰直角三角形,
从而c= 【补偿训练】已知椭圆G: (a>b>0)的离心率为
右焦点为 斜率为1的直线l与椭圆G交于A,B两点,以
AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程.
(2)求△PAB的面积.【解析】(1)由已知得
解得 又b2=a2-c2=4,
所以椭圆G的方程为
(2)设直线l的方程为y=x+m,
由 得4x2+6mx+3m2-12=0 ①设A,B的坐标分别为(x1,y1),(x2,y2)(x1<x2),
AB的中点为E(x0,y0),
则
因为AB是等腰△PAB的底边,所以PE⊥AB.
所以PE的斜率 解得m=2.
此时方程①为4x2+12x=0,
解得x1=-3,x2=0,所以y1=-1,y2=2.所以
此时,点P(-3,2)到直线AB:x-y+2=0的距离
所以△PAB的面积【拓展类型】椭圆中的最值问题
【备选例题】(1)斜率为1的直线l与椭圆 相交于A,B
两点,则|AB|的最大值为_________.
(2)如图,动圆C1:x2+y2=t2,1
②求直线AA1与直线A2B交点M的轨迹方程.【解析】(1)方法一:设直线l的方程为y=x+t,
由 消去y得
整理,得5x2+8tx+4(t2-1)=0.
因为Δ=64t2-80(t2-1)>0,所以设直线与椭圆交于A(x1,y1),B(x2,y2)两点,
则
所以|AB|=
=
当t=0时,|AB|为最大,即|AB|max=方法二:根据椭圆的对称性,当直线斜率固定时,直线过原点
时截椭圆所得弦长最长,将y=x代入 得交点坐标为
和 故
答案:(2)①设A(x0,y0)(-3
从而
当 时,Smax=6.
从而t= 时,矩形ABCD的面积最大,最大面积为6.②由A(x0,y0),B(x0,-y0),A1(-3,0),A2(3,0)知直线AA1的方程为
①
直线A2B的方程为 ②
由①②得 ③
又点A(x0,y0)在椭圆C上,故 ④
将④代入③得 (x<-3,y<0).
因此点M的轨迹方程为 (x<-3,y<0).【方法技巧】解决与椭圆有关的最值问题的三种方法
(1)定义法:利用定义转化为几何问题处理.
(2)数形结合法:利用数与形的结合,挖掘几何特征,进而求解.
(3)函数法:探求函数模型,转化为函数的最值问题来处理,注意椭圆的范围. 【规范解答】椭圆与平面向量的综合问题
【典例】(12分)设椭圆 (a>b>0)
的左焦点为F,离心率为 过点F且与x轴垂直的直线被椭圆
截得的线段长为
(1)求椭圆的方程.
(2)设A,B分别为椭圆的左、右顶点,过点F且斜率为k的直线与
椭圆交于C,D两点.若 AC·DB+AD·CB=8 求k的值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时,若求不出直线与椭圆交点的纵坐标,即得不出①处,则会导致求不出椭圆方程而本例不得分.
失分点2:若在②处化简整理结果时错误,则会导致下面运算全部错误,本例最多能得6分.
失分点3:若在③处向量的运算不能转化为坐标间关系,则得不出关于k的等量关系而失3~4分.【悟题】提措施,导方向
1.加强运算能力的培养
椭圆的综合问题,一般涉及的运算量较大,因此在平时学习中,要多注重运算能力的培养,防止因运算错误而失分,如本例(1)(2)问求解时,都涉及较大的运算量.2.向量关系的应用
在解析几何中,向量的运算常通过坐标的运算来实现,对向量
相等、向量的数量积、共线向量的坐标表示要熟练掌握,如本
例 是建立关于k的方程的关键.【类题试解】在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴上,短轴长为2,离心率为
(1)求椭圆C的方程.
(2)A,B为椭圆C上满足△AOB的面积为 的任意两点,E为线
段AB的中点,射线OE交椭圆C于点P,设 ,求实数t的值.【解析】(1)设椭圆C的方程为 (a>b>0),
由题意知 解得 因此椭圆C的方程为(2)当AB⊥x轴时,设A(x0,y0),B(x0,-y0),
由 得 或
由 =t(x0,0)=(tx0,0),得P(tx0,0),
又P在椭圆上,所以 所以 或
所以t=2或 (舍去负值).当AB不垂直于x轴时,设AB:y=kx+m,显然m≠0,代入椭圆方
程得(1+2k2)x2+4kmx+2(m2-1)=0. (*)
由三角形面积公式知, |xAyB-xByA|= |xA(kxB+m)-
xB(kxA+m)|= |m||xA-xB|=
所以,|xA-xB|= ?(xA+xB)2-4xAxB=
即整理得, ①
又 所以,
即
将其代入椭圆方程得 整理可得,
1+2k2=m2t2, ②联立①②,消去1+2k2,约分掉m2,移项整理得,3t4-16t2+16=0,
解之可得,t2=4或 均能使(*)式的Δ>0,所以t=2或 (舍去负值).
综上,t=2或
