2.4.1 抛物线及其标准方程 课件1
文档属性
| 名称 | 2.4.1 抛物线及其标准方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览






文档简介
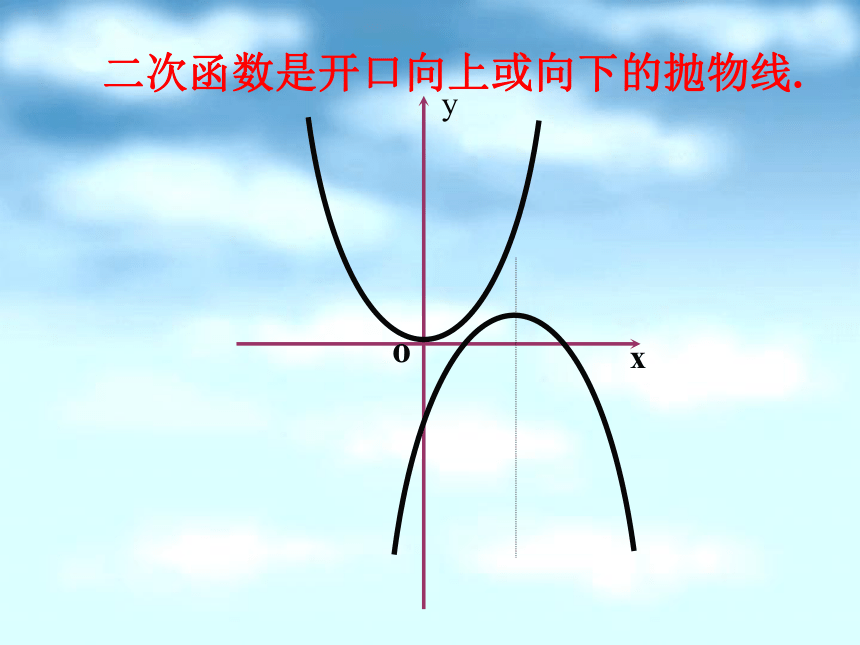
课件34张PPT。第二章 圆锥曲线与方程2.4.1 抛物线及其标准方程生活中存在着各种形式的抛物线我们对抛物线已有了哪些认识? 二次函数是开口向上或向下的抛物线.问题探究:
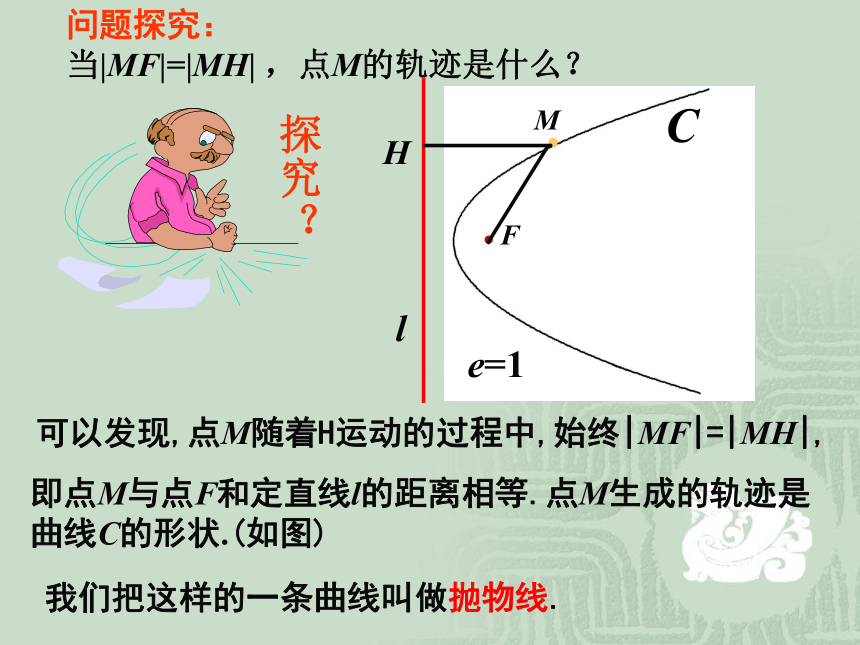
当|MF|=|MH| ,点M的轨迹是什么? 可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
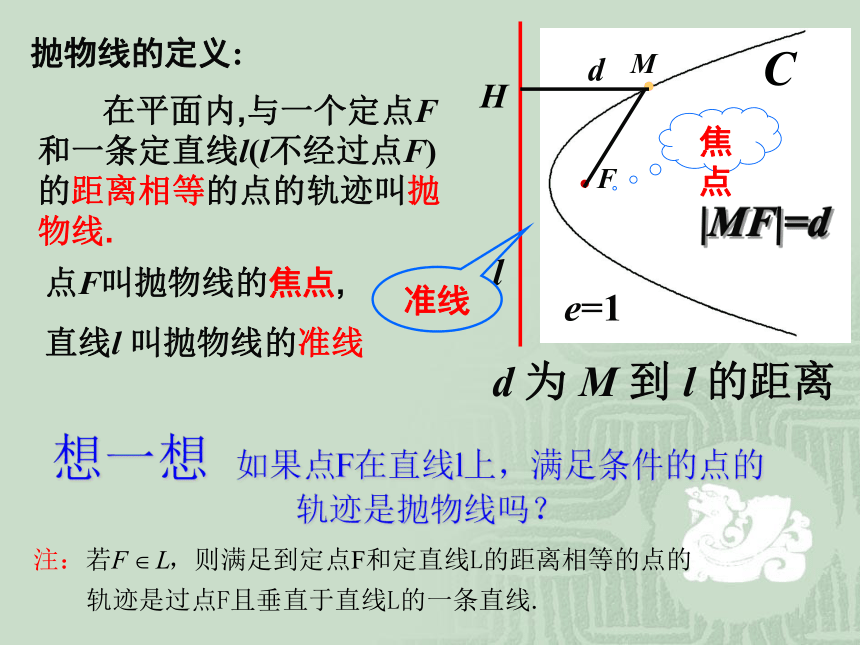
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)我们把这样的一条曲线叫做抛物线. 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,
直线l 叫抛物线的准线|MF|=dd 为 M 到 l 的距离准线焦点d抛物线的定义:想一想 如果点F在直线l上,满足条件的点的
轨迹是抛物线吗? 抛物线的定义
平面内与一个定点F和一条定直线l(不经过点F)_________的点的轨迹叫做抛物线.点F叫做抛物线的_____,直线l叫做
抛物线的_____ .
试一试:在抛物线定义中,若去掉条件“l不经过点F”,点的轨迹还是抛物线吗?
提示 当直线l经过点F时,点的轨迹是过定点F且垂直于定直线l的一条直线;l不经过点F时,点的轨迹是抛物线.1.距离相等焦点准线抛物线定义的理解
(2)在抛物线的定义中,定点F不能在直线l上,否则,动点M的轨迹就不是抛物线,而是过点F垂直于直线l的一条直线.如到点F(1,0)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y-1=0,轨迹为过点F且与直线l垂直的一条直线.
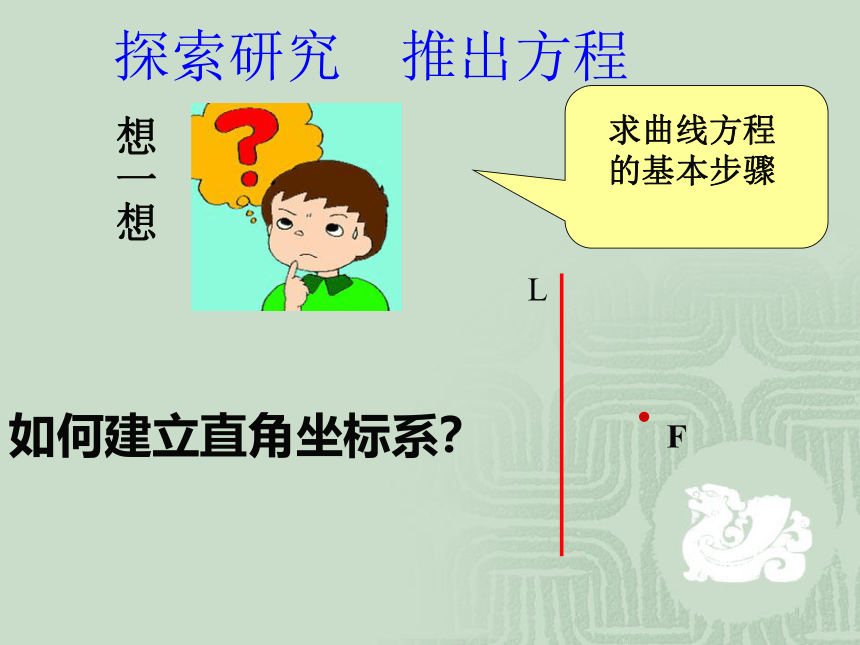
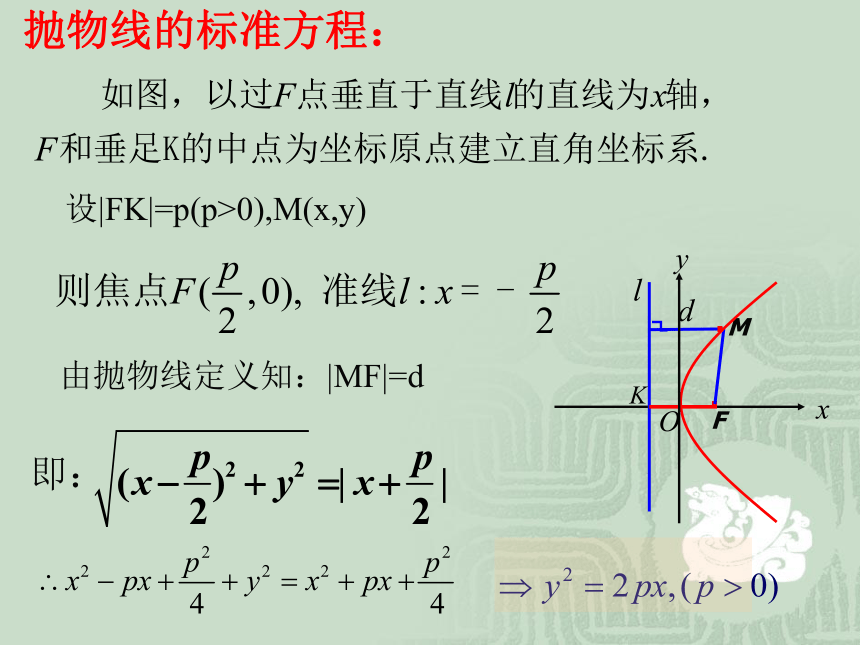
1.如何建立直角坐标系?想一想探索研究 推出方程.FM.抛物线的标准方程:设|FK|=p(p>0),M(x,y)由抛物线定义知:|MF|=d. ,叫作焦点在X轴正半轴上的
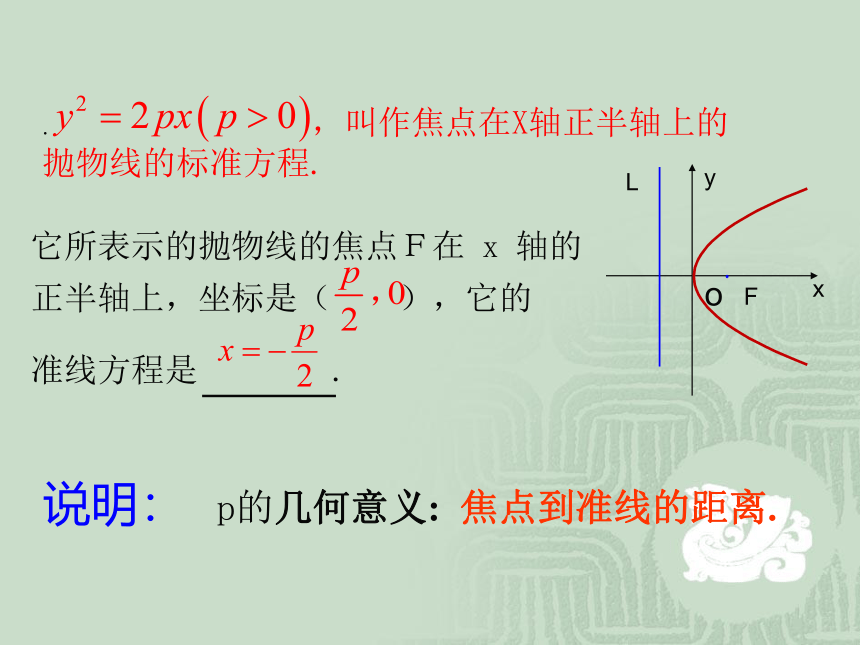
抛物线的标准方程.说明: 焦点到准线的距离.op的几何意义: 已知抛物线的标准方程, 求其焦点坐标和准线方程. 巩固练习1抛物线的标准方程
抛物线的焦点坐标和准线方程:关键:确定P的值反思总结. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.o一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.想一想:
抛物线的位置及其方程还有没有其它的形式? 问题:仿照前面求抛物线标准方程的方法,你能建立适当的坐标系,求下列后三幅图中抛物线的方程吗? 不同位置的抛物线标准方程 x轴的
正方向 x轴的
负方向 y轴的
正方向 y轴的
负方向y2=2pxy2=-2pxx2=2pyx2=-2py(P>0)抛物线标准方程的几种形式
2.y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)抛物线方程
左右型标准方程为
y2 =±2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =±2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型1、一次项的变量如为x(或y),则x轴(或y轴)为抛物线的对称轴,焦点就在对称轴上.
2、一次项的系数符号决定了开口方向.【小结】练习1:请判断下列抛物线的开口方向练习2:请判断下列抛物线的焦点坐标F(0,8)F(0, )F(-8,0)F( , 0)F(0, )F( , 0)练习3:请判断下列抛物线的准线方程F(0,8)F(0, )F(-8,0)F( , 0)F(0, )F( , 0)▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口椭 圆:看分母大小
双曲线:看符号P58思考: 二次函数 的图像为什么是抛物线? 当a>0时与当a<0时,结论都为:例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程.
(课本67页练习1)根据下列条件写出抛物线的标准方程;
(1)焦点是(3,0);
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
y2=12xy2=xy2=4xy2=-4xx2=4yx2=-4yF(5,0)F(0,-2)x=-5y=2(课本67页练习2)求下列抛物线的焦点坐标和准线方程:
(1)y2=20x
(2)x2= y
(3)2y2+5x=0
(4)x2+8y=0题型一 求抛物线的标准方程
分别求满足下列条件的抛物线的标准方程:
(3)过点A(2,3);
【例1】[思路探索] 式求抛物线方程要先确定其类型,并设出标准方程,再根据已知求出系数p.若类型不能确定,应分类讨论.(3)由题意,抛物线方程可设为y2=mx(m≠0)或x2=ny(n≠0),
将点A(2,3)的坐标代入,得
32=m·2或22=n·3,
如图,已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求此时P点坐标.
题型二 抛物线定义的应用【例2】[思路探索] 解题的关键是利用抛物线的定义得到|PA|+|PF|=|PA|+|PQ|,由图可知当A、P、Q三点共线时取最小值.
解 如图,作PQ⊥l于Q,由定义知,抛物线上点P到焦点F的距离等于点P到准线l的距离d,由图可知,求|PA|+|PF|的最小值的问题可转化为求|PA|+d的最小值的问题.
规律方法 抛物线的定义在解题中的作用,就是灵活地进行抛物线上的点到焦点的距离与到准线距离的转化,另外要注意平面几何知识的应用,如两点之间线段最短,三角形中三边间的不等关系,点与直线上点的连线垂线段最短等.
小 结 :1、学习好一个概念--抛物线2、掌握好一种题型--3、注重好一种思想--数形结合有关抛物线的标准方程和它的焦点坐标、准线方程的求法
当|MF|=|MH| ,点M的轨迹是什么? 可以发现,点M随着H运动的过程中,始终|MF|=|MH|,
即点M与点F和定直线l的距离相等.点M生成的轨迹是曲线C的形状.(如图)我们把这样的一条曲线叫做抛物线. 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F叫抛物线的焦点,
直线l 叫抛物线的准线|MF|=dd 为 M 到 l 的距离准线焦点d抛物线的定义:想一想 如果点F在直线l上,满足条件的点的
轨迹是抛物线吗? 抛物线的定义
平面内与一个定点F和一条定直线l(不经过点F)_________的点的轨迹叫做抛物线.点F叫做抛物线的_____,直线l叫做
抛物线的_____ .
试一试:在抛物线定义中,若去掉条件“l不经过点F”,点的轨迹还是抛物线吗?
提示 当直线l经过点F时,点的轨迹是过定点F且垂直于定直线l的一条直线;l不经过点F时,点的轨迹是抛物线.1.距离相等焦点准线抛物线定义的理解
(2)在抛物线的定义中,定点F不能在直线l上,否则,动点M的轨迹就不是抛物线,而是过点F垂直于直线l的一条直线.如到点F(1,0)与到直线l:x+y-1=0的距离相等的点的轨迹方程为x-y-1=0,轨迹为过点F且与直线l垂直的一条直线.
1.如何建立直角坐标系?想一想探索研究 推出方程.FM.抛物线的标准方程:设|FK|=p(p>0),M(x,y)由抛物线定义知:|MF|=d. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.说明: 焦点到准线的距离.op的几何意义: 已知抛物线的标准方程, 求其焦点坐标和准线方程. 巩固练习1抛物线的标准方程
抛物线的焦点坐标和准线方程:关键:确定P的值反思总结. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.o一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.想一想:
抛物线的位置及其方程还有没有其它的形式? 问题:仿照前面求抛物线标准方程的方法,你能建立适当的坐标系,求下列后三幅图中抛物线的方程吗? 不同位置的抛物线标准方程 x轴的
正方向 x轴的
负方向 y轴的
正方向 y轴的
负方向y2=2pxy2=-2pxx2=2pyx2=-2py(P>0)抛物线标准方程的几种形式
2.y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)抛物线方程
左右型标准方程为
y2 =±2px
(p>0)开口向右:
y2 =2px(x≥ 0)开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =±2py
(p>0)开口向上:
x2 =2py (y≥ 0)开口向下:
x2 = -2py (y≤0)抛物线的标准方程
上下型1、一次项的变量如为x(或y),则x轴(或y轴)为抛物线的对称轴,焦点就在对称轴上.
2、一次项的系数符号决定了开口方向.【小结】练习1:请判断下列抛物线的开口方向练习2:请判断下列抛物线的焦点坐标F(0,8)F(0, )F(-8,0)F( , 0)F(0, )F( , 0)练习3:请判断下列抛物线的准线方程F(0,8)F(0, )F(-8,0)F( , 0)F(0, )F( , 0)▲如何确定各曲线的焦点位置?
抛物线:1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口椭 圆:看分母大小
双曲线:看符号P58思考: 二次函数 的图像为什么是抛物线? 当a>0时与当a<0时,结论都为:例1 已知抛物线的标准方程是y2 = 6x,
求它的焦点坐标和准线方程;例2 已知抛物线的焦点坐标是F(0,-2)
求它的标准方程.
(课本67页练习1)根据下列条件写出抛物线的标准方程;
(1)焦点是(3,0);
(2)准线方程是x= - ;
(3)焦点到准线的距离是2;
y2=12xy2=xy2=4xy2=-4xx2=4yx2=-4yF(5,0)F(0,-2)x=-5y=2(课本67页练习2)求下列抛物线的焦点坐标和准线方程:
(1)y2=20x
(2)x2= y
(3)2y2+5x=0
(4)x2+8y=0题型一 求抛物线的标准方程
分别求满足下列条件的抛物线的标准方程:
(3)过点A(2,3);
【例1】[思路探索] 式求抛物线方程要先确定其类型,并设出标准方程,再根据已知求出系数p.若类型不能确定,应分类讨论.(3)由题意,抛物线方程可设为y2=mx(m≠0)或x2=ny(n≠0),
将点A(2,3)的坐标代入,得
32=m·2或22=n·3,
如图,已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|PA|+|PF|的最小值,并求此时P点坐标.
题型二 抛物线定义的应用【例2】[思路探索] 解题的关键是利用抛物线的定义得到|PA|+|PF|=|PA|+|PQ|,由图可知当A、P、Q三点共线时取最小值.
解 如图,作PQ⊥l于Q,由定义知,抛物线上点P到焦点F的距离等于点P到准线l的距离d,由图可知,求|PA|+|PF|的最小值的问题可转化为求|PA|+d的最小值的问题.
规律方法 抛物线的定义在解题中的作用,就是灵活地进行抛物线上的点到焦点的距离与到准线距离的转化,另外要注意平面几何知识的应用,如两点之间线段最短,三角形中三边间的不等关系,点与直线上点的连线垂线段最短等.
小 结 :1、学习好一个概念--抛物线2、掌握好一种题型--3、注重好一种思想--数形结合有关抛物线的标准方程和它的焦点坐标、准线方程的求法
