2.4.1 抛物线及其标准方程 课件2
文档属性
| 名称 | 2.4.1 抛物线及其标准方程 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 17:33:49 | ||
图片预览




文档简介
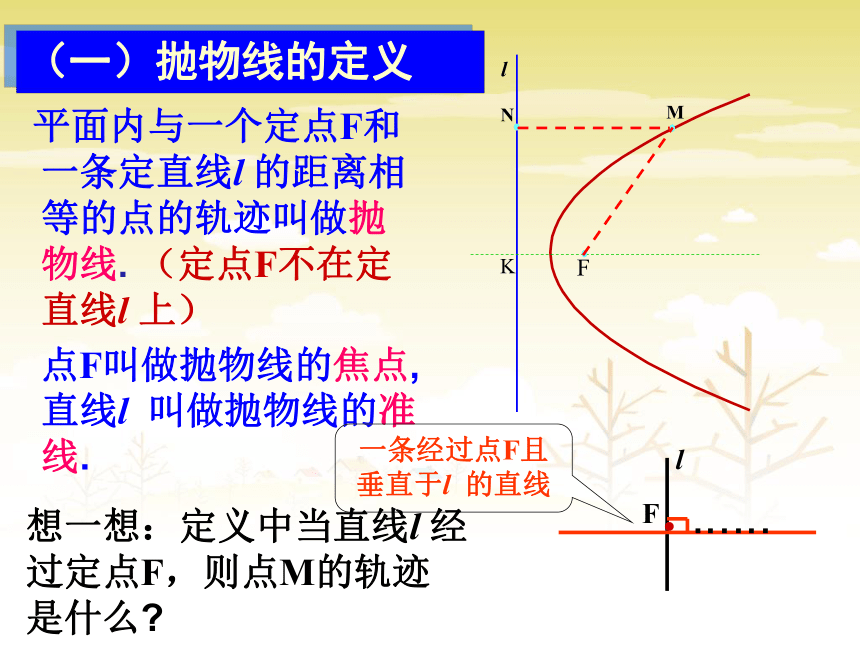
课件14张PPT。第二章 圆锥曲线与方程2.4.1 抛物线及其标准方程喷泉 平面内与一个定点F和一条定直线l 的距离相等的点的轨迹叫做抛物线. (定点F不在定直线l 上)
点F叫做抛物线的焦点,直线l 叫做抛物线的准线.
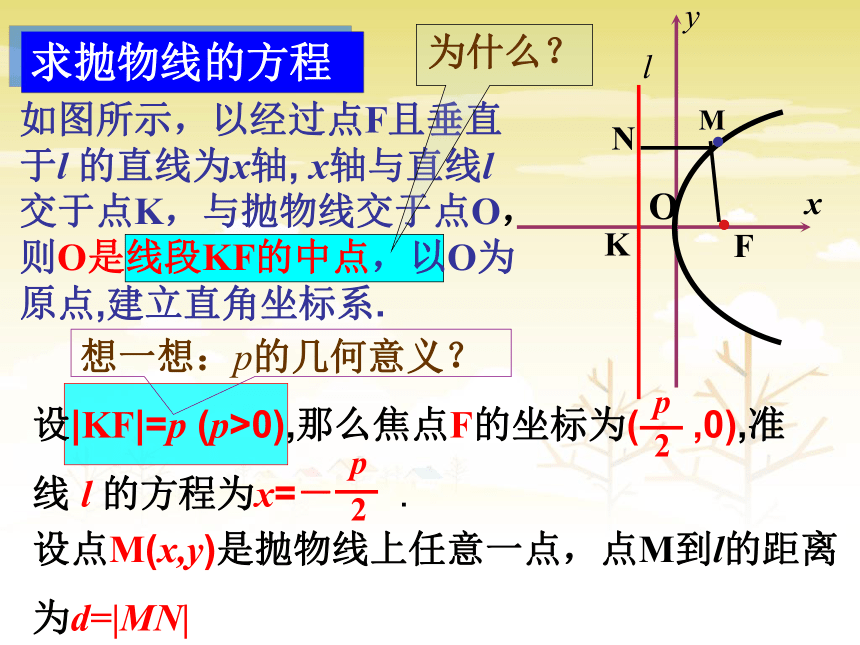
(一)抛物线的定义想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?一条经过点F且垂直于l 的直线······想一想:求抛物线方程时该如何建立直角坐标系?(二)抛物线的标准方程如图所示,以经过点F且垂直于l 的直线为x轴, x轴与直线l 交于点K,与抛物线交于点O,则O是线段KF的中点,以O为原点,建立直角坐标系.yOK设点M(x,y)是抛物线上任意一点,点M到l的距离
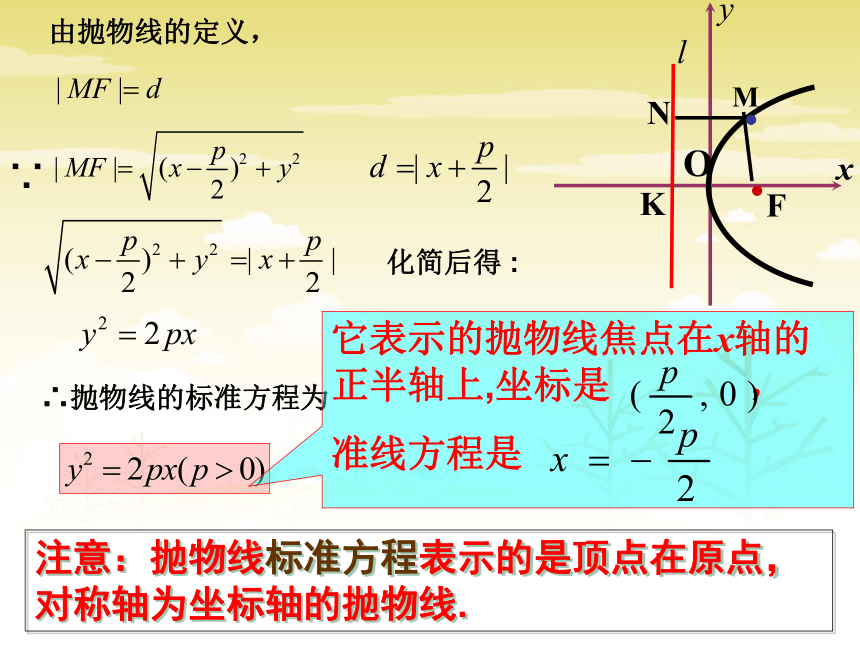
为d=|MN|想一想:p的几何意义?求抛物线的方程为什么?由抛物线的定义,∵化简后得 :∴抛物线的标准方程为它表示的抛物线焦点在x轴的正半轴上,坐标是 ,
准线方程是注意:抛物线标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线. 一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.想一想:怎样推导出其它几种形式的方程?yox四种抛物线的标准方程对比想一想: 如何判断上表中抛物线四种标准方程与图象的对应关系?第一:一次项变量决定对称轴.
第二:一次项系数的正负决定了开口方向.说明:当对称轴和开口方向确定好之后,抛物线图象就随之确定,根据图象可以很容易判断焦点坐标和准线方程.整个判断过程体现出从数到形,再由形到数的数形结合思想.(三)例题讲解例1.(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程. 解:(1)由方程可知,焦点在x轴正半轴上,坐标为 ,2p=6,
所以焦点坐标是 ,准线方程是 .(2) ∵抛物线焦点坐标为F(0,-2),
∴抛物线焦点在y轴负半轴上,设标准方程为x2=-2py,并且
∴2p=8,
∴抛物线的标准方程为x2=-8y.变式训练1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3) ;
(2)准线是 ;
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2 ;
(2)x2+8y=0;x2= -12yy2=2x焦点 ,准线焦点 ,准线感悟 :求抛物线的焦点坐标和准线方程要先化成抛物线的标准方程.感悟:用待定系数法求抛物线标准方程应先确定抛物线的形式,再求p值.强化提高根据下列条件写出抛物线的标准方程.
(1)焦点到准线的距离是2;
(2)焦点在直线3x-4y-12=0上.关键:理解p的几何意义,熟记标准方程四种形式关键:标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线解:∵焦点到准线的距离为2
∴p=2
又∵焦点的位置不确定
∴该抛物线标准方程有四种形式
y2=±2px , x2=±2py
此抛物线的标准方程有四种情况:
y2=±4x , x2=±4y 解:∵标准方程表示的抛物线的焦点在坐标轴上;
又∵抛物线的焦点在直线3x-4y-12=0上,
∴焦点就是直线与坐标轴的交点,直线3x-4y-12=0与x轴的交点是(4,0),与y轴的交点是(0,﹣3),
∴焦点坐标为(4,0)或(0,﹣3);
当焦点为(4,0)时标准方程为y2=16x ,
当焦点为(0,﹣3)时标准方程为x2= ﹣12y ,
综上,抛物线标准方程为 y2=16x或 x2= ﹣12y (四)课堂小结平面内与一个定点F的距离和一条定直线l 的距离相等的点的轨迹叫做抛物线.一个定义:两类问题:三项注意:四种形式:求抛物线标准方程;
已知方程求焦点坐标和准线方程.定义的前提条件:直线l 不经过点F;
p的几何意义:焦点到准线的距离;
标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线.抛物线的标准方程有四种: y2=2px(p>0)
y2= -2px(p>0)
x2=2py(p>0)
x2= -2py(p>0)
点F叫做抛物线的焦点,直线l 叫做抛物线的准线.
(一)抛物线的定义想一想:定义中当直线l 经过定点F,则点M的轨迹是什么?一条经过点F且垂直于l 的直线······想一想:求抛物线方程时该如何建立直角坐标系?(二)抛物线的标准方程如图所示,以经过点F且垂直于l 的直线为x轴, x轴与直线l 交于点K,与抛物线交于点O,则O是线段KF的中点,以O为原点,建立直角坐标系.yOK设点M(x,y)是抛物线上任意一点,点M到l的距离
为d=|MN|想一想:p的几何意义?求抛物线的方程为什么?由抛物线的定义,∵化简后得 :∴抛物线的标准方程为它表示的抛物线焦点在x轴的正半轴上,坐标是 ,
准线方程是注意:抛物线标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线. 一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式.想一想:怎样推导出其它几种形式的方程?yox四种抛物线的标准方程对比想一想: 如何判断上表中抛物线四种标准方程与图象的对应关系?第一:一次项变量决定对称轴.
第二:一次项系数的正负决定了开口方向.说明:当对称轴和开口方向确定好之后,抛物线图象就随之确定,根据图象可以很容易判断焦点坐标和准线方程.整个判断过程体现出从数到形,再由形到数的数形结合思想.(三)例题讲解例1.(1)已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2),求它的标准方程. 解:(1)由方程可知,焦点在x轴正半轴上,坐标为 ,2p=6,
所以焦点坐标是 ,准线方程是 .(2) ∵抛物线焦点坐标为F(0,-2),
∴抛物线焦点在y轴负半轴上,设标准方程为x2=-2py,并且
∴2p=8,
∴抛物线的标准方程为x2=-8y.变式训练1.根据下列条件写出抛物线的标准方程.
(1)焦点是(0,-3) ;
(2)准线是 ;
2.求下列抛物线的焦点坐标与准线方程.
(1)y=8x2 ;
(2)x2+8y=0;x2= -12yy2=2x焦点 ,准线焦点 ,准线感悟 :求抛物线的焦点坐标和准线方程要先化成抛物线的标准方程.感悟:用待定系数法求抛物线标准方程应先确定抛物线的形式,再求p值.强化提高根据下列条件写出抛物线的标准方程.
(1)焦点到准线的距离是2;
(2)焦点在直线3x-4y-12=0上.关键:理解p的几何意义,熟记标准方程四种形式关键:标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线解:∵焦点到准线的距离为2
∴p=2
又∵焦点的位置不确定
∴该抛物线标准方程有四种形式
y2=±2px , x2=±2py
此抛物线的标准方程有四种情况:
y2=±4x , x2=±4y 解:∵标准方程表示的抛物线的焦点在坐标轴上;
又∵抛物线的焦点在直线3x-4y-12=0上,
∴焦点就是直线与坐标轴的交点,直线3x-4y-12=0与x轴的交点是(4,0),与y轴的交点是(0,﹣3),
∴焦点坐标为(4,0)或(0,﹣3);
当焦点为(4,0)时标准方程为y2=16x ,
当焦点为(0,﹣3)时标准方程为x2= ﹣12y ,
综上,抛物线标准方程为 y2=16x或 x2= ﹣12y (四)课堂小结平面内与一个定点F的距离和一条定直线l 的距离相等的点的轨迹叫做抛物线.一个定义:两类问题:三项注意:四种形式:求抛物线标准方程;
已知方程求焦点坐标和准线方程.定义的前提条件:直线l 不经过点F;
p的几何意义:焦点到准线的距离;
标准方程表示的是顶点在原点,对称轴为坐标轴的抛物线.抛物线的标准方程有四种: y2=2px(p>0)
y2= -2px(p>0)
x2=2py(p>0)
x2= -2py(p>0)
