2.4.1 抛物线及其标准方程 课件5
文档属性
| 名称 | 2.4.1 抛物线及其标准方程 课件5 |  | |
| 格式 | zip | ||
| 文件大小 | 945.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 17:38:06 | ||
图片预览











文档简介
课件59张PPT。2.4 抛 物 线
2.4.1 抛物线及其标准方程1.抛物线的定义
(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)距离
_____的点的轨迹.
(2)焦点:____叫做抛物线的焦点.
(3)准线:_____叫做抛物线的准线.相等点F直线l2.抛物线的标准方程1.判一判(正确的打“√”,错误的打“×”)
(1)标准方程y2=2px(p>0)中的p的几何意义是焦点到准线的距离.( )
(2)抛物线的焦点位置由一次项及一次项系数的正负决定.( )
(3)平面内到一定点距离与到一定直线距离相等的点的轨迹是抛物线.( )【解析】(1)正确.抛物线的标准方程中p(p>0)即为焦点到准线的距离,故该说法正确.
(2)正确.一次项决定焦点所在的坐标轴,一次项系数的正负决定焦点是在正半轴或负半轴上,故该说法正确.
(3)错误.当定点在定直线上时,不表示抛物线,故该说法错误.
答案:(1)√ (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)抛物线y2=4x的焦点坐标为 ;准线方程为 .
(2)若抛物线的方程为x=2ay2(a>0),则焦点到准线的距离p= .
(3)焦点坐标为(0,2)的抛物线的标准方程为 .【解析】(1)因为y2=4x,所以p=2,所以焦点坐标为(1,0),
准线方程为x=-1.
答案:(1,0) x=-1
(2)因为x=2ay2(a>0),所以
由 所以
答案:(3)因为焦点坐标为(0,2),故标准方程可设为x2=2py(p>0),
其中 所以p=4.
故标准方程为x2=8y.
答案:x2=8y 【要点探究】
知识点 抛物线的定义及标准方程
1.对抛物线定义的两点说明
(1)定直线l不经过定点F.
(2)定义中包含三个定值,分别为一个定点,一条定直线及一个确定的比值.2.抛物线标准方程的特点
(1)是关于x,y的二元二次方程.
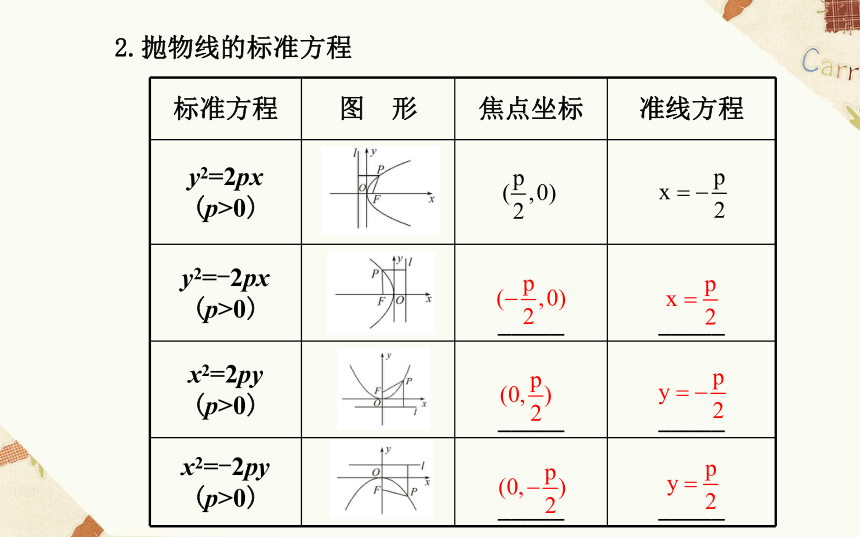
(2)p的几何意义是焦点到准线的距离.3.四种位置的抛物线标准方程的对比
(1)共同点:①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的 .
(2)不同点:①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2.
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.【知识拓展】抛物线与二次函数的关系
二次函数的解析式为y=ax2+bx+c(a≠0),当b,c为0时,
y=ax2表示焦点在y轴上的抛物线,标准方程为x2= a>0时
抛物线开口向上,a<0时,抛物线开口向下,当抛物线的开口
方向向左或向右时,方程为y2=2px,表示一条曲线,不能称为
函数.【微思考】
(1)定义中若去掉条件“l不经过F”,则此时点的轨迹是什么?
提示:若点F在直线l上,满足条件的动点P的轨迹是过点F且垂直于l的直线,而不是抛物线.
(2)确定抛物线的标准方程时,一般需要确定几个量?
提示:确定两个量,一个是p,另一个是一次项系数的正负.【即时练】
1.以 为焦点的抛物线的标准方程是_________.
2.若抛物线y2=8x上一点P到其焦点的距离为9,则点P的坐标为
__________.【解析】1.因为焦点F为 所以抛物线方程可设为y2=
-2px(p>0),由 所以
故标准方程为y2=-3x.
答案:y2=-3x2.根据抛物线的定义,点P到抛物线准线的距离为9,
设P(x0,y0),则
即x0+2=9,所以x0=7,代入y2=8x,
得
所以P点坐标为
答案: 【题型示范】
类型一 求抛物线的标准方程
【典例1】
(1)已知双曲线C1: (a>0,b>0)的离心率为2.若抛物
线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则
抛物线C2的方程为( )(2)求适合下列条件的抛物线的标准方程:
①过点M(-6,6);
②焦点F在直线l:3x-2y-6=0上.【解题探究】1.题(1)中抛物线的焦点坐标是什么?
2.题(2)①已知抛物线上一点,如何确定开口方向?
②中抛物线的焦点坐标是什么?
【探究提示】1.抛物线的焦点坐标为
2.①中的点在第二象限,故抛物线的开口向上或向左;
②中抛物线的焦点坐标为(0,-3)或(2,0).【自主解答】(1)选D.抛物线的焦点坐标为 双曲线的渐
近线方程为 不妨取 即bx-ay=0,焦点到渐近线
的距离为
即 所以
又双曲线的离心率为2,所以
所以p=8,所以抛物线方程为x2=16y.(2)①由于点M(-6,6)在第二象限,
所以过M的抛物线开口向左或开口向上.
若开口向左,焦点在x轴上,
设其方程为y2=-2px(p>0),
将点M(-6,6)代入可得36=-2p×(-6),
所以p=3,抛物线方程为y2=-6x;若开口向上,焦点在y轴上,
设其方程为x2=2py(p>0),
将M(-6,6)代入可得36=2p×6,所以p=3.
所以抛物线的方程为x2=6y.
综上所述,抛物线的标准方程为y2=-6x或x2=6y.②直线l与x轴的交点为(2,0),
若抛物线的焦点在x轴上,
所以抛物线的焦点是F(2,0),
所以
抛物线的方程为y2=8x.直线l与y轴的交点是(0,-3),
若抛物线的焦点在y轴上,
即抛物线的焦点是F(0,-3),
所以
所以抛物线的标准方程为x2=-12y.
综上,所求抛物线的标准方程为y2=8x或x2=-12y.【方法技巧】求抛物线标准方程的方法
(1)当焦点位置确定时,可利用待定系数法,设出抛物线的标准方程,由已知条件建立关于参数p的方程,求出p的值,进而写出抛物线的标准方程.
(2)当焦点位置不确定时,可设抛物线的方程为y2=mx或x2=ny,利用已知条件求出m,n的值.【变式训练】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x【解析】选C.由题意知: 准线方程为 则由抛物
线的定义知, 设以MF为直径的圆的圆心为
所以圆方程为 又因为过点(0,2),所以
yM=4,又因为点M在C上,所以 解得p=2或p=8,所
以抛物线C的方程为y2=4x或y2=16x.【补偿训练】抛物线顶点在原点,对称轴是x轴,点
到焦点的距离为6,求抛物线的标准方程.
【解析】设焦点F(a,0),
即a2+10a+9=0,解得a=-1或a=-9.
当焦点为F(-1,0)时,p=2,抛物线的开口向左,其方程为
y2=-4x;当焦点为F(-9,0)时,p=18,抛物线开口向左,其方
程为y2=-36x.类型二 根据标准方程求焦点坐标和准线方程
【典例2】
(1)已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则抛物线的准线方程为 .
(2)指出下列抛物线的焦点坐标和准线方程.
①y= x2.
②x=ay2(a≠0).【解题探究】1.题(1)由圆与抛物线的准线相切,能得出什么结论?
2.题(2)当抛物线方程中含参数时,如何求焦点和准线?
【探究提示】1.可得出圆心到准线的距离等于圆的半径.
2.如果抛物线方程中含参数,要先把其化成标准方程,对参数应分类讨论,再求焦点和准线.【自主解答】(1)圆x2+y2-6x-7=0可化为(x-3)2+y2=16,所以圆
心为(3,0),半径为4,因抛物线y2=2px(p>0)的准线
与圆相切,故 得p=2或p=-14(舍),所以准线方程为
x=-1.
答案:x=-1(2)①抛物线 的标准形式为x2=4y,
所以p=2,
所以焦点坐标是(0,1),准线方程是y=-1.
②抛物线x=ay2(a≠0)的标准形式为
所以当a>0时, 抛物线开口向右,
所以焦点坐标是 准线方程是
当a<0时, 抛物线开口向左,
所以焦点坐标是 准线方程是
综上所述,当a≠0时,抛物线x=ay2的焦点坐标为 准线
方程为【延伸探究】题(2)②中,把方程改为x2=ay(a≠0),结果如
何?
【解析】方程x2=ay是抛物线的标准形式,由方程知,其焦点
在y轴上,其焦点坐标为 准线方程为【方法技巧】求焦点坐标和准线方程的步骤【变式训练】抛物线y= x2的准线方程是
( )
A.y=-1 B.y=-2 C.x=-1 D.x=-2
【解题指南】将抛物线化为标准形式即可得出.
【解析】选A.y= x2?x2=4y,
所以抛物线的准线方程是y=-1.【补偿训练】抛物线 的准线方程是( )
【解析】选C.由 得x2=-8y,
所以准线方程为类型三 抛物线的实际应用
【典例3】
(1)汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处,已知灯口的直径是24cm,灯深10cm,那么灯泡与反射镜顶点(即截得抛物线顶点)间的距离是 .
(2)某抛物线形拱桥跨度是20米,拱桥高度是4米,在建桥时,每4米需用一根支柱支撑,求其中最长支柱的长.【解题探究】1.题(1)中应如何建系求解较简单?
2.题(2)中最长支柱应在什么位置?
【探究提示】1.以反射镜的轴即抛物线的对称轴为x轴,抛物线的顶点为坐标原点建立坐标系.
2.最长支柱应是离拱高4米的位置2米处的支柱.【自主解答】(1)取反射镜的轴即抛物线的对称轴为x轴,抛物线的顶点为坐标原点,建立直角坐标系xOy,如图所示.
因灯口直径|AB|=24,灯深|OP|=10,
所以点A的坐标是(10,12).
设抛物线的方程为y2=2px(p>0),
由点A(10,12)在抛物线上,得122=2p×10,所以p=7.2.
所以抛物线的焦点F的坐标为(3.6,0).因此灯泡与反射镜顶点间的距离是3.6cm.
答案:3.6cm(2)如图,建立直角坐标系,设抛物线方程为x2=-2py(p>0).依题意知,点P(10,-4)在抛物线上,
所以100=-2p×(-4),2p=25.
即抛物线方程为x2=-25y.
因为每4米需用一根支柱支撑,
所以支柱横坐标分别为-6,-2,2,6.
由图知,AB是最长的支柱之一.设点B的坐标为(2,yB),
代入x2=-25y,得
所以
即最长支柱的长为3.84米.【方法技巧】求解抛物线实际应用题的五个步骤【变式训练】如图是一种加热水和食物
的太阳灶,上面装有可旋转的抛物面形
的反光镜,镜的轴截面是抛物线的一部
分,盛水和食物的容器放在抛物线的焦
点处,容器由若干根等长的铁筋焊接在
一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,则每根铁筋的长度为 米.【解题指南】先建立直角坐标系,然后设出抛物线的标准方程结合已知条件进而可得到p的值,从而可确定抛物线的方程和焦点的位置.根据盛水的容器在焦点处,结合两点间的距离公式可得到每根铁筋的长度.【解析】如图,在反光镜的轴截面内建立
直角坐标系,使反光镜的顶点(即抛物线
的顶点)与原点重合,x轴垂直于镜口直径.
由已知,得A点坐标是(2,6),
设抛物线方程为y2=2px(p>0),
则36=2p×2,p=9.所以所求抛物线的标准方程是y2=18x,
焦点坐标是
因为盛水和食物的容器在焦点处,
所以A,F两点间的距离即为每根铁筋长.
故每根铁筋的长度是6.5米.
答案:6.5【补偿训练】河上有一抛物线形拱桥,当水面距拱顶5 m时,
水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的
部分高 问水面上涨到与抛物线拱顶相距______ m时,小
船不能通航.【解题指南】先建立直角坐标系,设抛物线的标准方程,将点
(4,-5)代入求得p,得到抛物线方程,再把点(2,y1)代入,
求得y1,进而求得 得到答案.【解析】建立直角坐标系,
设抛物线方程为x2=-2py(p>0).
将点(4,-5)代入求得
所以
将点(2,y1)代入方程求得
所以
答案:2【巧思妙解】巧用抛物线的定义解题
【典例】已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.【教你审题】【常规解法】设抛物线方程为y2=-2px(p>0),则焦点
由题意可得 解得 或
故所求的抛物线方程为y2=-8x.所以m的值为【巧妙解法】
设抛物线的方程为y2=-2px(p>0),
则 故p=4.
所以抛物线的方程为y2=-8x.将点(-3,m)代入抛物线方程得【方法对比】
常规解法思路易得出,但需要解二元二次方程组,稍有疏忽,则会解出错误的结果.而巧妙解法则是利用抛物线的定义,得出简单一元一次方程,不易出错,解法简单.【教你一招】
巧用定义解与抛物线有关的问题
由抛物线的定义,可将两点间的距离转化为点到直线的距离,将二次问题转化为一次问题,凡涉及焦点距离问题可转化为到准线的距离求解.如本例即可转化为点M到准线的距离为5求解. 【类题试解】已知抛物线y=4x2上一点M到焦点的距离为1,求
点M的坐标.
【常规解法】将抛物线y=4x2化为标准形式为 故焦点
坐标为 设M(x0,y0),
则 解得 所以【巧妙解法】将抛物线y=4x2化为标准形式为 故焦点
坐标为 设M(x0,y0),
则 所以 代入抛物线方程得
所以
故点M坐标为
2.4.1 抛物线及其标准方程1.抛物线的定义
(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)距离
_____的点的轨迹.
(2)焦点:____叫做抛物线的焦点.
(3)准线:_____叫做抛物线的准线.相等点F直线l2.抛物线的标准方程1.判一判(正确的打“√”,错误的打“×”)
(1)标准方程y2=2px(p>0)中的p的几何意义是焦点到准线的距离.( )
(2)抛物线的焦点位置由一次项及一次项系数的正负决定.( )
(3)平面内到一定点距离与到一定直线距离相等的点的轨迹是抛物线.( )【解析】(1)正确.抛物线的标准方程中p(p>0)即为焦点到准线的距离,故该说法正确.
(2)正确.一次项决定焦点所在的坐标轴,一次项系数的正负决定焦点是在正半轴或负半轴上,故该说法正确.
(3)错误.当定点在定直线上时,不表示抛物线,故该说法错误.
答案:(1)√ (2)√ (3)×2.做一做(请把正确的答案写在横线上)
(1)抛物线y2=4x的焦点坐标为 ;准线方程为 .
(2)若抛物线的方程为x=2ay2(a>0),则焦点到准线的距离p= .
(3)焦点坐标为(0,2)的抛物线的标准方程为 .【解析】(1)因为y2=4x,所以p=2,所以焦点坐标为(1,0),
准线方程为x=-1.
答案:(1,0) x=-1
(2)因为x=2ay2(a>0),所以
由 所以
答案:(3)因为焦点坐标为(0,2),故标准方程可设为x2=2py(p>0),
其中 所以p=4.
故标准方程为x2=8y.
答案:x2=8y 【要点探究】
知识点 抛物线的定义及标准方程
1.对抛物线定义的两点说明
(1)定直线l不经过定点F.
(2)定义中包含三个定值,分别为一个定点,一条定直线及一个确定的比值.2.抛物线标准方程的特点
(1)是关于x,y的二元二次方程.
(2)p的几何意义是焦点到准线的距离.3.四种位置的抛物线标准方程的对比
(1)共同点:①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的 .
(2)不同点:①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的右端为±2py,左端为x2.
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右端取正号;开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.【知识拓展】抛物线与二次函数的关系
二次函数的解析式为y=ax2+bx+c(a≠0),当b,c为0时,
y=ax2表示焦点在y轴上的抛物线,标准方程为x2= a>0时
抛物线开口向上,a<0时,抛物线开口向下,当抛物线的开口
方向向左或向右时,方程为y2=2px,表示一条曲线,不能称为
函数.【微思考】
(1)定义中若去掉条件“l不经过F”,则此时点的轨迹是什么?
提示:若点F在直线l上,满足条件的动点P的轨迹是过点F且垂直于l的直线,而不是抛物线.
(2)确定抛物线的标准方程时,一般需要确定几个量?
提示:确定两个量,一个是p,另一个是一次项系数的正负.【即时练】
1.以 为焦点的抛物线的标准方程是_________.
2.若抛物线y2=8x上一点P到其焦点的距离为9,则点P的坐标为
__________.【解析】1.因为焦点F为 所以抛物线方程可设为y2=
-2px(p>0),由 所以
故标准方程为y2=-3x.
答案:y2=-3x2.根据抛物线的定义,点P到抛物线准线的距离为9,
设P(x0,y0),则
即x0+2=9,所以x0=7,代入y2=8x,
得
所以P点坐标为
答案: 【题型示范】
类型一 求抛物线的标准方程
【典例1】
(1)已知双曲线C1: (a>0,b>0)的离心率为2.若抛物
线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则
抛物线C2的方程为( )(2)求适合下列条件的抛物线的标准方程:
①过点M(-6,6);
②焦点F在直线l:3x-2y-6=0上.【解题探究】1.题(1)中抛物线的焦点坐标是什么?
2.题(2)①已知抛物线上一点,如何确定开口方向?
②中抛物线的焦点坐标是什么?
【探究提示】1.抛物线的焦点坐标为
2.①中的点在第二象限,故抛物线的开口向上或向左;
②中抛物线的焦点坐标为(0,-3)或(2,0).【自主解答】(1)选D.抛物线的焦点坐标为 双曲线的渐
近线方程为 不妨取 即bx-ay=0,焦点到渐近线
的距离为
即 所以
又双曲线的离心率为2,所以
所以p=8,所以抛物线方程为x2=16y.(2)①由于点M(-6,6)在第二象限,
所以过M的抛物线开口向左或开口向上.
若开口向左,焦点在x轴上,
设其方程为y2=-2px(p>0),
将点M(-6,6)代入可得36=-2p×(-6),
所以p=3,抛物线方程为y2=-6x;若开口向上,焦点在y轴上,
设其方程为x2=2py(p>0),
将M(-6,6)代入可得36=2p×6,所以p=3.
所以抛物线的方程为x2=6y.
综上所述,抛物线的标准方程为y2=-6x或x2=6y.②直线l与x轴的交点为(2,0),
若抛物线的焦点在x轴上,
所以抛物线的焦点是F(2,0),
所以
抛物线的方程为y2=8x.直线l与y轴的交点是(0,-3),
若抛物线的焦点在y轴上,
即抛物线的焦点是F(0,-3),
所以
所以抛物线的标准方程为x2=-12y.
综上,所求抛物线的标准方程为y2=8x或x2=-12y.【方法技巧】求抛物线标准方程的方法
(1)当焦点位置确定时,可利用待定系数法,设出抛物线的标准方程,由已知条件建立关于参数p的方程,求出p的值,进而写出抛物线的标准方程.
(2)当焦点位置不确定时,可设抛物线的方程为y2=mx或x2=ny,利用已知条件求出m,n的值.【变式训练】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x【解析】选C.由题意知: 准线方程为 则由抛物
线的定义知, 设以MF为直径的圆的圆心为
所以圆方程为 又因为过点(0,2),所以
yM=4,又因为点M在C上,所以 解得p=2或p=8,所
以抛物线C的方程为y2=4x或y2=16x.【补偿训练】抛物线顶点在原点,对称轴是x轴,点
到焦点的距离为6,求抛物线的标准方程.
【解析】设焦点F(a,0),
即a2+10a+9=0,解得a=-1或a=-9.
当焦点为F(-1,0)时,p=2,抛物线的开口向左,其方程为
y2=-4x;当焦点为F(-9,0)时,p=18,抛物线开口向左,其方
程为y2=-36x.类型二 根据标准方程求焦点坐标和准线方程
【典例2】
(1)已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则抛物线的准线方程为 .
(2)指出下列抛物线的焦点坐标和准线方程.
①y= x2.
②x=ay2(a≠0).【解题探究】1.题(1)由圆与抛物线的准线相切,能得出什么结论?
2.题(2)当抛物线方程中含参数时,如何求焦点和准线?
【探究提示】1.可得出圆心到准线的距离等于圆的半径.
2.如果抛物线方程中含参数,要先把其化成标准方程,对参数应分类讨论,再求焦点和准线.【自主解答】(1)圆x2+y2-6x-7=0可化为(x-3)2+y2=16,所以圆
心为(3,0),半径为4,因抛物线y2=2px(p>0)的准线
与圆相切,故 得p=2或p=-14(舍),所以准线方程为
x=-1.
答案:x=-1(2)①抛物线 的标准形式为x2=4y,
所以p=2,
所以焦点坐标是(0,1),准线方程是y=-1.
②抛物线x=ay2(a≠0)的标准形式为
所以当a>0时, 抛物线开口向右,
所以焦点坐标是 准线方程是
当a<0时, 抛物线开口向左,
所以焦点坐标是 准线方程是
综上所述,当a≠0时,抛物线x=ay2的焦点坐标为 准线
方程为【延伸探究】题(2)②中,把方程改为x2=ay(a≠0),结果如
何?
【解析】方程x2=ay是抛物线的标准形式,由方程知,其焦点
在y轴上,其焦点坐标为 准线方程为【方法技巧】求焦点坐标和准线方程的步骤【变式训练】抛物线y= x2的准线方程是
( )
A.y=-1 B.y=-2 C.x=-1 D.x=-2
【解题指南】将抛物线化为标准形式即可得出.
【解析】选A.y= x2?x2=4y,
所以抛物线的准线方程是y=-1.【补偿训练】抛物线 的准线方程是( )
【解析】选C.由 得x2=-8y,
所以准线方程为类型三 抛物线的实际应用
【典例3】
(1)汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯口所在的圆面与反射镜的轴垂直,灯泡位于抛物线焦点处,已知灯口的直径是24cm,灯深10cm,那么灯泡与反射镜顶点(即截得抛物线顶点)间的距离是 .
(2)某抛物线形拱桥跨度是20米,拱桥高度是4米,在建桥时,每4米需用一根支柱支撑,求其中最长支柱的长.【解题探究】1.题(1)中应如何建系求解较简单?
2.题(2)中最长支柱应在什么位置?
【探究提示】1.以反射镜的轴即抛物线的对称轴为x轴,抛物线的顶点为坐标原点建立坐标系.
2.最长支柱应是离拱高4米的位置2米处的支柱.【自主解答】(1)取反射镜的轴即抛物线的对称轴为x轴,抛物线的顶点为坐标原点,建立直角坐标系xOy,如图所示.
因灯口直径|AB|=24,灯深|OP|=10,
所以点A的坐标是(10,12).
设抛物线的方程为y2=2px(p>0),
由点A(10,12)在抛物线上,得122=2p×10,所以p=7.2.
所以抛物线的焦点F的坐标为(3.6,0).因此灯泡与反射镜顶点间的距离是3.6cm.
答案:3.6cm(2)如图,建立直角坐标系,设抛物线方程为x2=-2py(p>0).依题意知,点P(10,-4)在抛物线上,
所以100=-2p×(-4),2p=25.
即抛物线方程为x2=-25y.
因为每4米需用一根支柱支撑,
所以支柱横坐标分别为-6,-2,2,6.
由图知,AB是最长的支柱之一.设点B的坐标为(2,yB),
代入x2=-25y,得
所以
即最长支柱的长为3.84米.【方法技巧】求解抛物线实际应用题的五个步骤【变式训练】如图是一种加热水和食物
的太阳灶,上面装有可旋转的抛物面形
的反光镜,镜的轴截面是抛物线的一部
分,盛水和食物的容器放在抛物线的焦
点处,容器由若干根等长的铁筋焊接在
一起的架子支撑.已知镜口圆的直径为12米,镜深2米,若把盛水和食物的容器近似地看作点,则每根铁筋的长度为 米.【解题指南】先建立直角坐标系,然后设出抛物线的标准方程结合已知条件进而可得到p的值,从而可确定抛物线的方程和焦点的位置.根据盛水的容器在焦点处,结合两点间的距离公式可得到每根铁筋的长度.【解析】如图,在反光镜的轴截面内建立
直角坐标系,使反光镜的顶点(即抛物线
的顶点)与原点重合,x轴垂直于镜口直径.
由已知,得A点坐标是(2,6),
设抛物线方程为y2=2px(p>0),
则36=2p×2,p=9.所以所求抛物线的标准方程是y2=18x,
焦点坐标是
因为盛水和食物的容器在焦点处,
所以A,F两点间的距离即为每根铁筋长.
故每根铁筋的长度是6.5米.
答案:6.5【补偿训练】河上有一抛物线形拱桥,当水面距拱顶5 m时,
水面宽为8 m,一小船宽4 m,高2 m,载货后船露出水面上的
部分高 问水面上涨到与抛物线拱顶相距______ m时,小
船不能通航.【解题指南】先建立直角坐标系,设抛物线的标准方程,将点
(4,-5)代入求得p,得到抛物线方程,再把点(2,y1)代入,
求得y1,进而求得 得到答案.【解析】建立直角坐标系,
设抛物线方程为x2=-2py(p>0).
将点(4,-5)代入求得
所以
将点(2,y1)代入方程求得
所以
答案:2【巧思妙解】巧用抛物线的定义解题
【典例】已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.【教你审题】【常规解法】设抛物线方程为y2=-2px(p>0),则焦点
由题意可得 解得 或
故所求的抛物线方程为y2=-8x.所以m的值为【巧妙解法】
设抛物线的方程为y2=-2px(p>0),
则 故p=4.
所以抛物线的方程为y2=-8x.将点(-3,m)代入抛物线方程得【方法对比】
常规解法思路易得出,但需要解二元二次方程组,稍有疏忽,则会解出错误的结果.而巧妙解法则是利用抛物线的定义,得出简单一元一次方程,不易出错,解法简单.【教你一招】
巧用定义解与抛物线有关的问题
由抛物线的定义,可将两点间的距离转化为点到直线的距离,将二次问题转化为一次问题,凡涉及焦点距离问题可转化为到准线的距离求解.如本例即可转化为点M到准线的距离为5求解. 【类题试解】已知抛物线y=4x2上一点M到焦点的距离为1,求
点M的坐标.
【常规解法】将抛物线y=4x2化为标准形式为 故焦点
坐标为 设M(x0,y0),
则 解得 所以【巧妙解法】将抛物线y=4x2化为标准形式为 故焦点
坐标为 设M(x0,y0),
则 所以 代入抛物线方程得
所以
故点M坐标为
