2.4.2 抛物线的简单几何性质 课件1
文档属性
| 名称 | 2.4.2 抛物线的简单几何性质 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 17:39:21 | ||
图片预览







文档简介
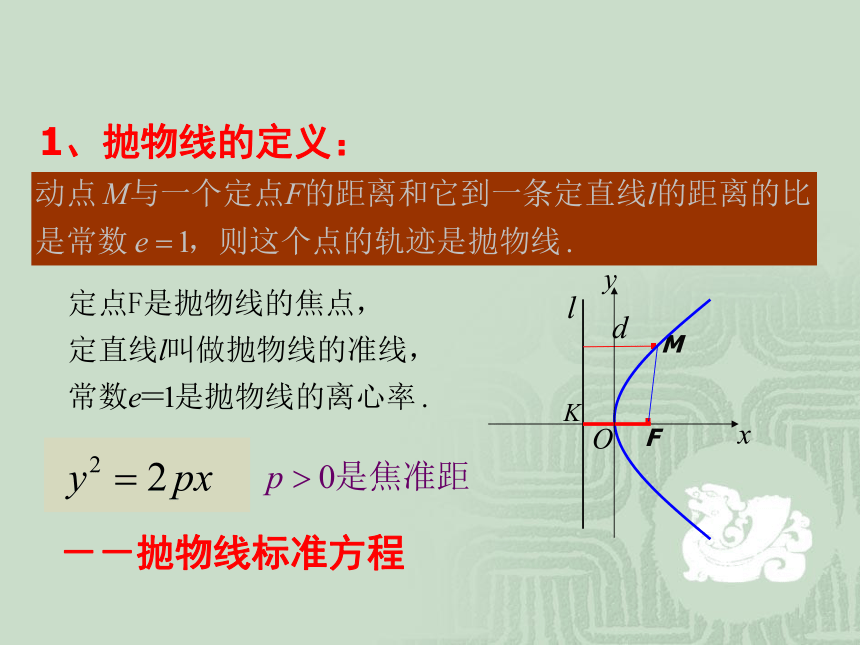
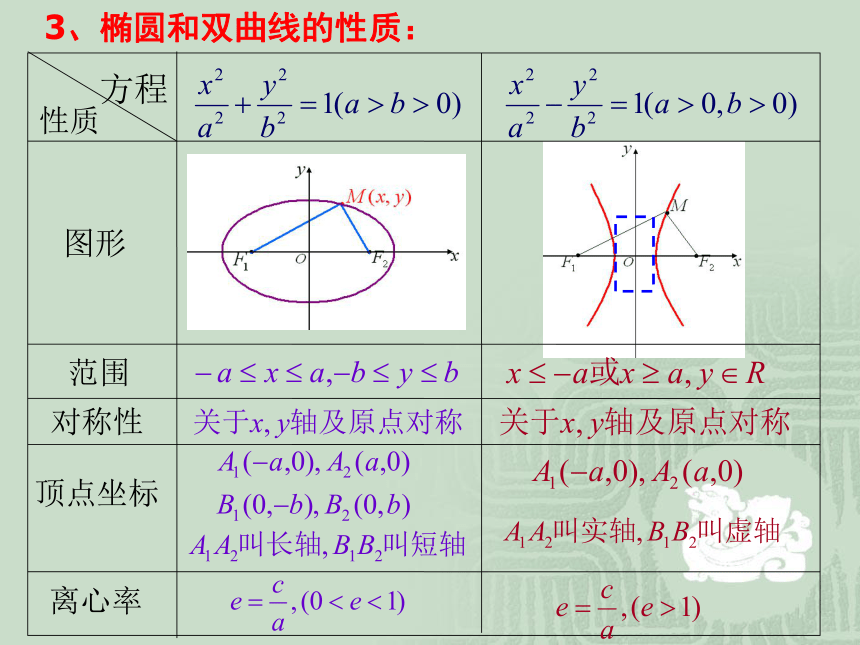
课件26张PPT。第二章 圆锥曲线与方程2.4.2 抛物线的简单几何性质--抛物线标准方程1、抛物线的定义:2、抛物线的标准方程:3、椭圆和双曲线的性质:结合抛物线y2=2px(p>0)的标准方程和图形,探索其的几何性质:
(1)范围
(2)对称性
(3)顶点类比探索x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点.(4)离心率
(5)焦半径
(6)通径e=1通过焦点且垂直对称轴的直线,与抛物线相交于两点,连接这两点的线段叫做抛物线的通径.|PF|=x0+p/2FP通径的长度:2Py2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的e=1;5.抛物线标准方程中的p对抛物线开口的影响.P越大,开口越开阔---本质是成比例地放大!例1. 顶点在坐标原点,对称轴是坐标轴,并且过点
M(2, )的抛物线有几条,求它的标准方程. 当焦点在x[或y]轴上,开口方向不定时,
设为y2=mx(m ≠0) [或x2=my (m≠0)],可
避免讨论!思考:通径是抛物线的焦点弦中最短的弦吗? 与直线的倾斜角无关!
很奇怪!解完后回味一下,这是一个很好的解题习惯,利于提高!这一结论非常奇妙,变中有不变,动中有不动. 坐标法是一种非常好的证明,你还有没有其他好方法呢?本题几何法也是一个极佳的思维!判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总结:一、抛物线的几何性质:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)A1二、抛物线的焦点弦:通径就是过焦点且垂直于x轴的线段长为2p即为 的最小值
(1)范围
(2)对称性
(3)顶点类比探索x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点.(4)离心率
(5)焦半径
(6)通径e=1通过焦点且垂直对称轴的直线,与抛物线相交于两点,连接这两点的线段叫做抛物线的通径.|PF|=x0+p/2FP通径的长度:2Py2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)特点:1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的e=1;5.抛物线标准方程中的p对抛物线开口的影响.P越大,开口越开阔---本质是成比例地放大!例1. 顶点在坐标原点,对称轴是坐标轴,并且过点
M(2, )的抛物线有几条,求它的标准方程. 当焦点在x[或y]轴上,开口方向不定时,
设为y2=mx(m ≠0) [或x2=my (m≠0)],可
避免讨论!思考:通径是抛物线的焦点弦中最短的弦吗? 与直线的倾斜角无关!
很奇怪!解完后回味一下,这是一个很好的解题习惯,利于提高!这一结论非常奇妙,变中有不变,动中有不动. 坐标法是一种非常好的证明,你还有没有其他好方法呢?本题几何法也是一个极佳的思维!判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总结:一、抛物线的几何性质:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)A1二、抛物线的焦点弦:通径就是过焦点且垂直于x轴的线段长为2p即为 的最小值
