2.4.2 抛物线的简单几何性质 课件2
文档属性
| 名称 | 2.4.2 抛物线的简单几何性质 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览




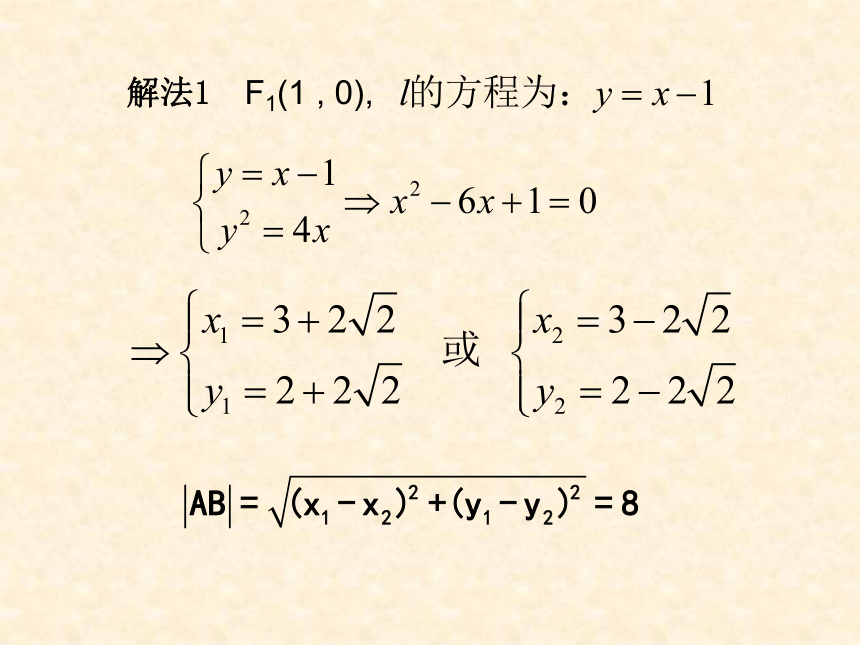
文档简介
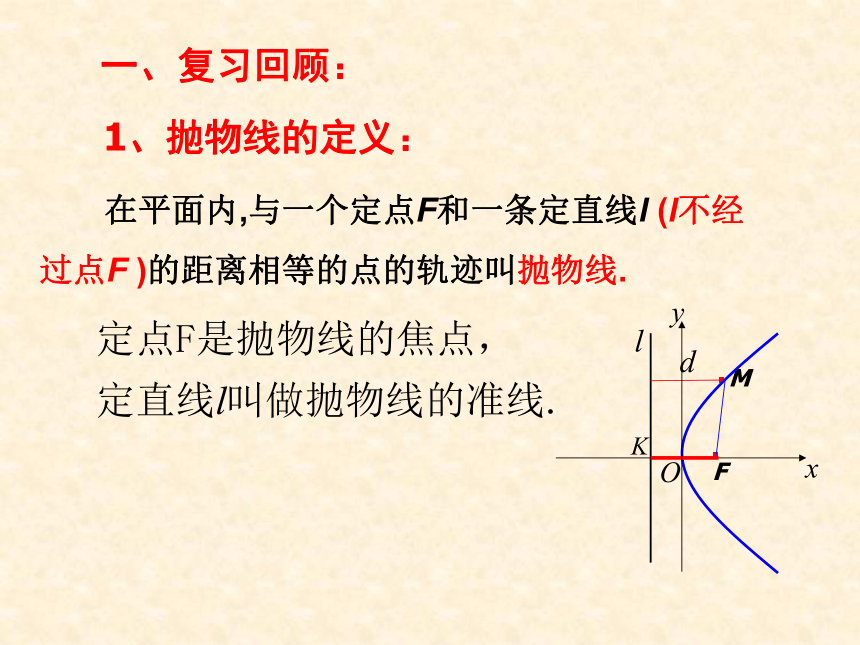
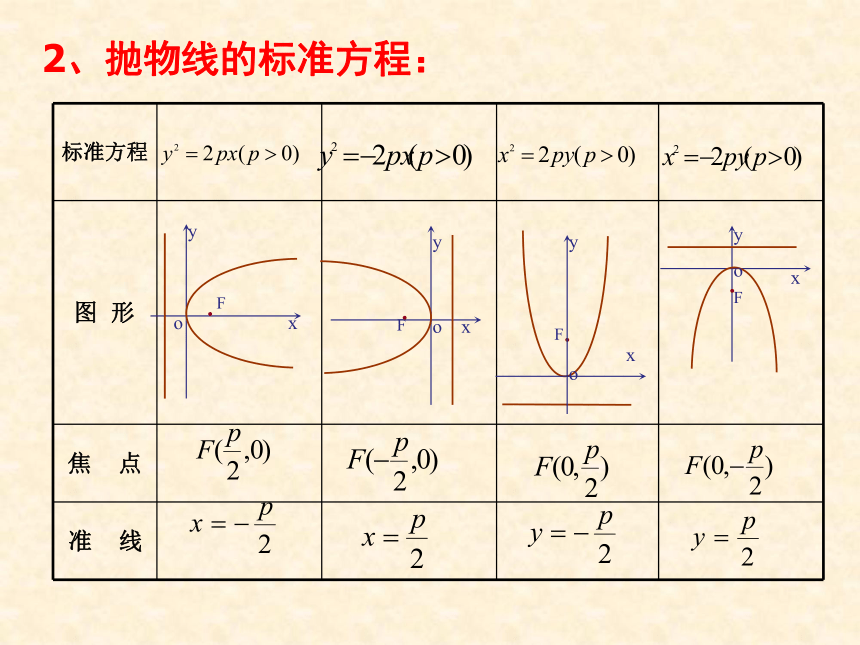
课件25张PPT。第二章 圆锥曲线与方程2.4.2 抛物线的简单几何性质一、复习回顾:1、抛物线的定义: 在平面内,与一个定点F和一条定直线l (l不经过点F )的距离相等的点的轨迹叫抛物线.2、抛物线的标准方程:(1)范围
(2)对称性
(3)顶点x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点.二、讲授新课: 抛物线上的点到焦点的距离和它到准
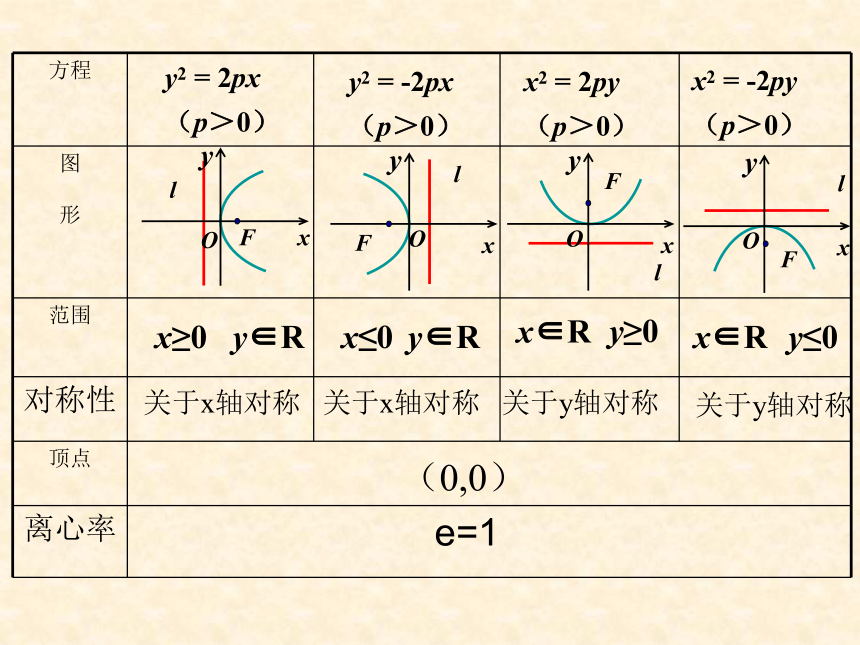
线的距离的比,叫做抛物线的离心率,用e表示,(4)离心率由抛物线的定义可知,e=1 抛物线y2=2px(p>0)
的几何性质:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
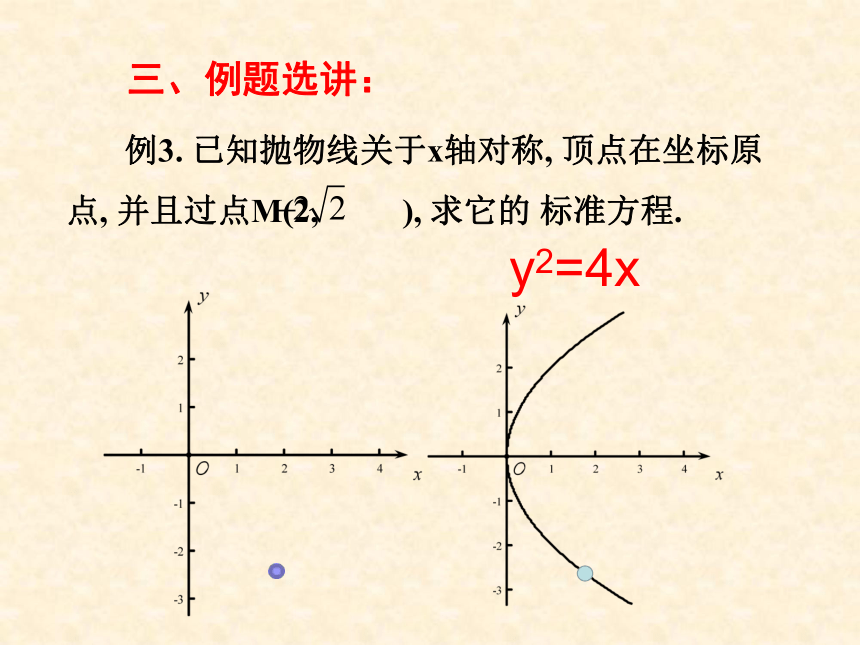
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)e=1三、例题选讲:y2=4x 解法1 F1(1 , 0), 解法2 F1(1 , 0), 解法3 F1(1 , 0), |AB |= |AF|+ |BF |
= |AA1 |+ |BB1 |
=(x1+1)+(x2+1)
=x1+x2+2=8解法4H? ? 例 抛物线y2=4x的焦点为F,
点M在抛物线上运动, A(2,2), 试求
|MA|+|MF|的最小值.MFAA1M1解 |MA|+|MF|
=|MA|+|MM1|
≥|AA1|=3即 |MA|+|MF|的最小值为3. 练习 抛物线y2=4x上的
点M到准线距离为d, A(2,4),
试求|MA|+d的最小值.MFAd?? 例5 过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴. 所以,直线DB平行于抛物线的对称轴. 例5.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.xOyFABD当直线AB存在斜率时,设AB为与y2=2px联立,得?yAyB=-p2当直线AB存在斜率时,结论显然成立. 所以,直线DB平
行于抛物线的对称轴.⑴只有一个公共点⑵有两个公共点⑶没有公共点判断直线与圆锥曲线位置关系的操作程序:把直线方程代入曲线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总 结
(2)对称性
(3)顶点x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.抛物线和它的轴的交点.二、讲授新课: 抛物线上的点到焦点的距离和它到准
线的距离的比,叫做抛物线的离心率,用e表示,(4)离心率由抛物线的定义可知,e=1 抛物线y2=2px(p>0)
的几何性质:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)e=1三、例题选讲:y2=4x 解法1 F1(1 , 0), 解法2 F1(1 , 0), 解法3 F1(1 , 0), |AB |= |AF|+ |BF |
= |AA1 |+ |BB1 |
=(x1+1)+(x2+1)
=x1+x2+2=8解法4H? ? 例 抛物线y2=4x的焦点为F,
点M在抛物线上运动, A(2,2), 试求
|MA|+|MF|的最小值.MFAA1M1解 |MA|+|MF|
=|MA|+|MM1|
≥|AA1|=3即 |MA|+|MF|的最小值为3. 练习 抛物线y2=4x上的
点M到准线距离为d, A(2,4),
试求|MA|+d的最小值.MFAd?? 例5 过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴. 所以,直线DB平行于抛物线的对称轴. 例5.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.xOyFABD当直线AB存在斜率时,设AB为与y2=2px联立,得?yAyB=-p2当直线AB存在斜率时,结论显然成立. 所以,直线DB平
行于抛物线的对称轴.⑴只有一个公共点⑵有两个公共点⑶没有公共点判断直线与圆锥曲线位置关系的操作程序:把直线方程代入曲线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总 结
