2.4.2 圆锥曲线与方程 课件1
文档属性
| 名称 | 2.4.2 圆锥曲线与方程 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览








文档简介
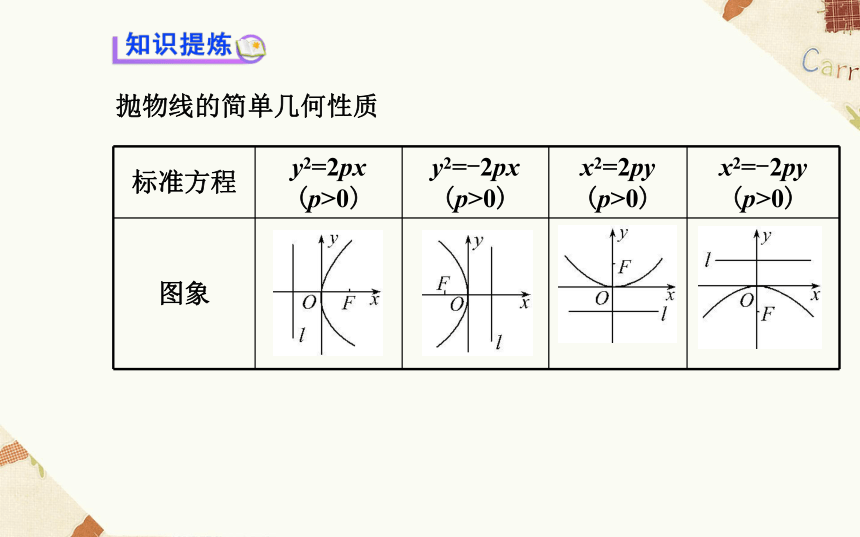
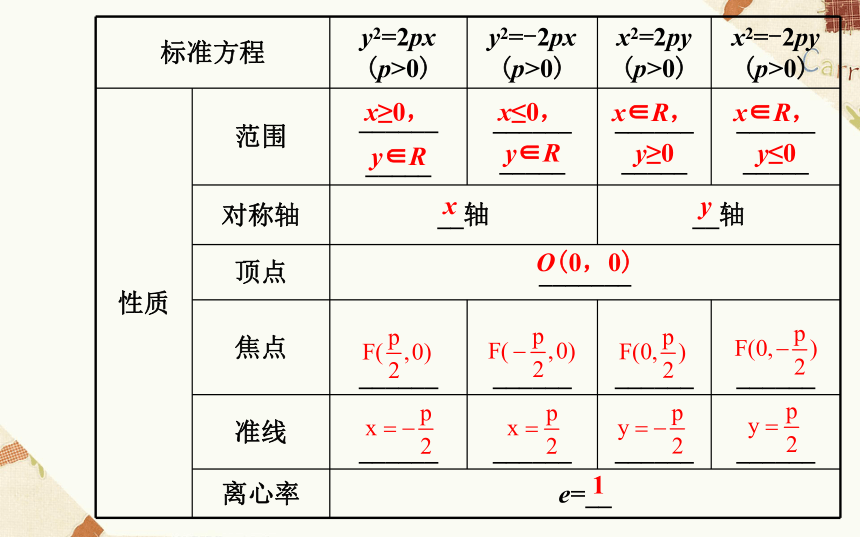
课件68张PPT。2.4.2 抛物线的简单几何性质抛物线的简单几何性质x≥0,y∈Rx≤0,y∈Rx∈R,y≥0x∈R,y≤0xyO(0,0)11.判一判(正确的打“√”,错误的打“×”)
(1)抛物线是中心对称图形.( )
(2)抛物线的范围是x∈R.( )
(3)抛物线是轴对称图形.( )【解析】(1)错误.在抛物线方程中,以-x代x,-y代y,方程发生了变化,故抛物线不是中心对称图形,故此说法错误.
(2)错误.抛物线的方程不同,其范围就不一样,如y2=2px(p>0)的范围是x≥0,y∈R,故此说法错误.
(3)正确.抛物线y2=±2px(p>0)的对称轴为x轴,抛物线x2=±2py(p>0)的对称轴为y轴,故此说法正确.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)顶点在原点,对称轴为y轴且过(4,1)的抛物线方程是 .
(2)已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则p= .
(3)抛物线y=2px2(p>0)的对称轴为 .【解析】(1)由已知可设抛物线的方程为x2=ay,将点(4,1)代入,得a=16,故方程为x2=16y.
答案:x2=16y(2)y2=2px(p>0)的焦点为 由题意得
解得p=4或p=-12(舍去).
答案:4
(3)由y=2px2(p>0),得
故对称轴为y轴.
答案:y轴【要点探究】
知识点 抛物线的简单几何性质
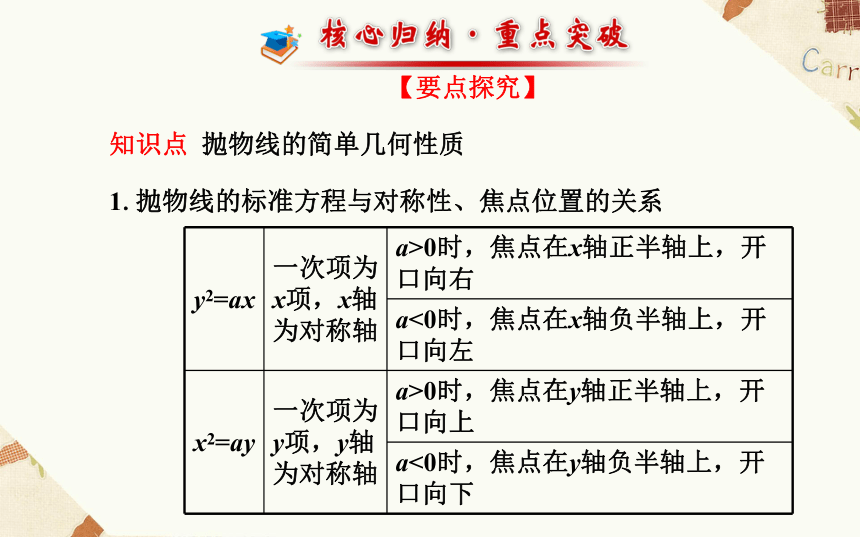
1.抛物线的标准方程与对称性、焦点位置的关系2.抛物线的图象具有的特征
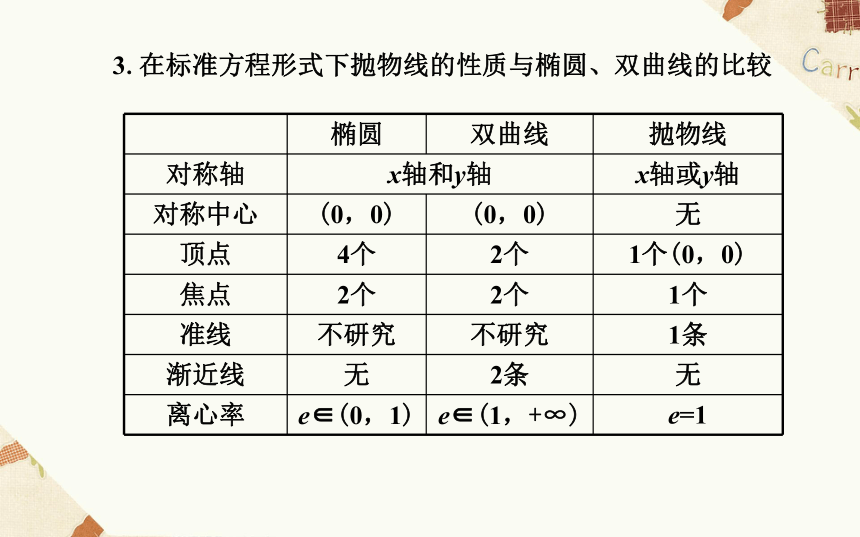
抛物线是轴对称图形,其对称轴为x轴或y轴,只有一个顶点,一个焦点,一条准线,并且离心率为1.3.在标准方程形式下抛物线的性质与椭圆、双曲线的比较【知识拓展】抛物线的通径【微思考】
(1)影响抛物线开口大小的量是什么,是如何影响的?
提示:参数p影响抛物线开口大小,p值越大,抛物线的开口越开阔,p越小,开口越扁狭.(2)点P(x0,y0)与抛物线y2=2px(p>0)的关系有哪些?分别满足什么条件?
提示:①点P(x0,y0)在抛物线y2=2px(p>0)内部?y02<2px0;
②点P(x0,y0)在抛物线y2=2px(p>0)上?y02=2px0;
③点P(x0,y0)在抛物线y2=2px(p>0)外部?y02>2px0.【即时练】
已知抛物线y2=6x,判断下列点与该抛物线的关系.
(1)P1(1, ).(2)P2(2,3).(3)P3(1,3).
【解析】将点的坐标分别代入抛物线y2=6x的方程,可知P1在
抛物线上,P2在抛物线内部,P3在抛物线外部.【题型示范】
类型一 焦半径和焦点弦问题
【典例1】
(1)过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2),若x1+x2=6,那么|AB|等于( )
A.10 B.8 C.6 D.4(2)已知抛物线y2=2px(p>0),直线l经过其焦点且与x轴垂直,并交抛物线于A,B两点,若|AB|=10,P为抛物线的准线上一点,则△ABP的面积为( )
A.20 B.25 C.30 D.50【解题探究】1.题(1)过焦点的弦问题一般如何处理?
2.题(2)中焦点到准线的距离等于多少?
【探究提示】1.过焦点的弦问题一般可转化为焦半径问题求解.
2.焦点到准线的距离等于p.【自主解答】(1)选B.由抛物线y2=4x,得p=2,
设抛物线的焦点为F,则|AB|=|AF|+|FB|=
=x1+x2+p=6+2=8.
(2)选B.因为直线l过抛物线y2=2px(p>0)的焦点且与x轴垂直,
并且交抛物线于A,B两点,则|AB|=2p=10,所以p=5,故抛物
线的方程为y2=10x,P为抛物线的准线上一点.P到直线AB的距
离为p=5,则△ABP的面积为 ×10×5=25.【方法技巧】
1.抛物线的焦半径
(1)抛物线的焦半径是指以抛物线上任意一点与抛物线焦点为
端点的线段.
(2)抛物线的焦半径公式:P(x0,y0)为抛物线上一点,F为焦点.
①若抛物线y2=2px(p>0),则|PF|=
②若抛物线y2=-2px(p>0),则|PF|=
③若抛物线x2=2py(p>0),则|PF|=
④若抛物线x2=-2py(p>0),则|PF|=2.过焦点的弦长的求解方法
设过抛物线y2=2px(p>0)的焦点的弦的端点为A(x1,y1), B(x2,y2),则|AB|=x1+x2+p,然后利用弦所在直线方程与抛物线方程联立、消元,由根与系数的关系求出x1+x2即可.【变式训练】抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线的方程.
【解题指南】联立方程组,由过焦点的弦长公式表示出弦长,解方程求出参数值,从而得出抛物线的标准方程.【解析】若抛物线开口向右,
如图.
设抛物线的方程为y2=2px(p>0),
则直线方程为设直线交抛物线于A(x1,y1),
B(x2,y2)两点,
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|
=
即x1+x2+p=8. ①
又A(x1,y1),B(x2,y2)是抛物线和直线的交点,
由 消去y,得
所以x1+x2=3p.将其代入①,得p=2.
所以所求抛物线的方程为y2=4x.
当抛物线的开口向左时,同理可求得抛物线的方程为y2=-4x.
综上,抛物线的方程为y2=4x或y2=-4x. 【补偿训练】AB是过抛物线y2=2px(p>0)焦点F的一条弦,且
|AF|=1,|BF|= 求抛物线及直线AB的方程.
【解题指南】设出A,B两点的坐标,根据抛物线定义可分别表
示出|AF|和|BF|,进而可求得|AF|+|BF|,求得x1+x2的表达
式,表示出|AF|·|BF|,建立等式求得p,则抛物线方程可得.
再由|AB|= 得sin2θ= 从而利用特殊角的三角函
数求出直线AB的斜率,由点斜式方程写出直线AB的方程.【解析】设A(x1,y1),B(x2,y2),
则|AF|= |BF|=
则|AF|+|BF|=x1+x2+p=
所以x1+x2=
因为|AF|≠|BF|,
所以过焦点 的直线斜率存在且不为0,则可设AB的方程
为又因为A,B两点是直线AB与抛物线的交点,则
所以x1·x2=
由|AF|·|BF|=
得
即 所以
抛物线方程为y2=x.设直线AB的倾斜角为θ,
又根据两点间的距离公式得|AB|2=(y2-y1)2+(x2-x1)2=(tan2θ+
1)(x2-x1)2,
由于直线AB过点
设直线AB的方程为 与抛物线方程联立得到:tan2θx2-(tan2θ+2)px+ p2tan2θ=0,
那么(x2-x1)2=(x2+x1)2-4x1x2
==4p2(tan2θ+1)×
那么|AB|2=(tan2θ+1)(x2-x1)2
=(tan2θ+1)×4p2(tan2θ+1)×所以|AB|=
由|AB|= 得
所以
所以θ=60°或120°,得
所以直线AB的方程为类型二 抛物线性质的应用
【典例2】
(1)抛物线y2=4x的焦点为F,准线为l,点A是抛物线上一点,且∠AFO=120°(O为坐标原点),AK⊥l,垂足为K,则△AKF的面积是 .
(2)已知正三角形AOB的一个顶点O位于坐标原点,另外两个顶点A,B在抛物线y2=2px(p>0)上,求这个三角形的边长.【解题探究】1.题(1)由题设条件,要求△AKF的面积,只需求出什么?
2.题(2)三角形的另两个顶点应满足什么关系?
【探究提示】1.根据题设条件,要求△AKF的面积,只需求出点A的坐标即可.
2.根据抛物线的对称性及三角形为正三角形,故A,B两点应关于x轴对称.【自主解答】(1)如图,
设A(x0,y0),
过A作AH⊥x轴于H,
在Rt△AFH中,|FH|=x0-1,
由∠AFO=120°得∠AFH=60°,
故所以点A的坐标为
将此代入抛物线方程可得3x02-10x0+3=0,
解得x0=3或x0= (舍),故S△AKF=
答案:(2)如图所示,设正三角形OAB的顶点A,B在抛物线上,且坐标分别为(x1,y1),(x2,y2),y12=2px1,y22=2px2.
又因为|OA|=|OB|,
所以x12+y12=x22+y22,
即x12-x22+2px1-2px2=0.
所以(x1-x2)(x1+x2+2p)=0.
因为x1>0,x2>0,2p>0,
所以x1+x2+2p≠0.所以x1=x2.即A,B两点关于x轴对称,则∠AOx=30°,
所以AB⊥x轴,所以y1=x1tan 30°=
又因为x1= 所以y1=
而|AB|=2y1= 即为所求边长.【延伸探究】题(2)中若△AOB为直角三角形,且∠AOB=90°,判断直线AB是否恒过定点?
【解析】直线AB恒过定点(2p,0).设
由OA⊥OB,故kOA·kOB=-1,得:
即y1·y2=-4p2.所以直线AB的方程为
即
=
将y1·y2=-4p2代入上式得
故直线AB恒过定点(2p,0).【方法技巧】利用抛物线的性质可以解决的问题
(1)对称性:解决抛物线的内接三角形问题.
(2)焦点、准线:解决与抛物线的定义有关的问题.
(3)范围:解决与抛物线有关的最值问题.
(4)焦点:解决焦点弦问题.【变式训练】已知直线l过坐标原点,
抛物线C顶点在原点,焦点在x轴正半
轴上.若点A(-1,0)和点B(0,8)关于
l的对称点都在C上,求直线l和抛物线
C的方程.【解题指南】先设出抛物线的标准方程和直线l的方程,根据A′,B′分别是A,B关于l的对称点,进而可知A′A⊥l,进而可得直线A′A的方程,把两直线方程联立求得交点M的坐标,进而根据M为AA′的中点,求得A′点的坐标和B′点的坐标,分别代入抛物线方程求得p的表达式,最后联立求得k,进而求得p,则直线和抛物线的方程可得.【解析】依题设抛物线C的方程可写为
y2=2px(p>0),
且x轴和y轴不是所求直线,又l过原点,
因而可设l的方程为y=kx(k≠0),①
设A′,B′分别是A,B关于l的对称点,因而A′A⊥l,直线
A′A的方程为 ②
由①②联立解得AA′与l的交点M的坐标为又M为AA′的中点,从而点A′的横坐标为
纵坐标为
同理得点B′的横、纵坐标分别为又A′,B′均在抛物线y2=2px(p>0)上,
由③得
由此知k≠±1,即
同理由④得 即
从而 整理得k2-k-1=0,
解得但当 时,由③知
这与点A′在抛物线y2=2px(p>0)上矛盾,故舍去
所以 则直线l的方程为
将 代入 ⑤求得
所以直线方程为 抛物线方程为【补偿训练】已知A,B是抛物线y2=2px(p>0)上两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点,求直线AB的方程.【解析】如图所示.设A(x0,y0),
由题意可知B(x0,-y0),
又 是△AOB的垂心,
则AF⊥OB,所以kAF·kOB=-1,
即 所以y02=
又y02=2px0,所以
因此直线AB的方程为类型三 抛物线中的定值与最值问题
【典例3】
(1)已知抛物线y2=2px(p>0)的经过焦点的弦AB的两端点坐标分别为A(x1,y1),B(x2,y2),则 的值一定等于( )
A.4 B.-4 C.p2 D.-p2
(2)抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐
标是( )
A.( ,1) B.(0,0) C.(1,2) D.(1,4)【解题探究】1.题(1)x1·x2可否用y1y2表示?
2.题(2)中抛物线的方程是否是标准方程,抛物线上的任意一点到直线y=4x-5的距离如何表示?【探究提示】1.能.由A,B在抛物线上,故
所以
2.已知的方程不是标准形式,可化为 可设抛物线上的
一点为(x,4x2),则其到直线的距离为【自主解答】(1)选B.由抛物线y2=2px(p>0),得焦点坐标为
设过焦点的弦AB所在直线方程为
由 消去x得:y2-2pmy-p2=0,
所以y1·y2=-p2.
由A(x1,y1),B(x2,y2)在抛物线上,故
所以(2)选A.方法一:设抛物线上点的坐标为(x,4x2),其中x∈R,
由点到直线的距离公式得
所以当 时,d最小.这时点的坐标为方法二:设与y=4x-5平行的抛物线y=4x2的切线方程为y=4x+m,
由 得4x2-4x-m=0.
再由Δ=16-4×4×(-m)=0得m=-1.
这时切点为 切点 到y=4x-5的距离最小.【方法技巧】抛物线中最值的求解策略
(1)可借助于抛物线的有关知识转化为函数的最值求解,但要注意抛物线的范围.
(2)当条件中有关于抛物线上的点P到焦点F的距离问题一定要考虑抛物线的定义,注意点P到F的距离与点P到准线距离的转化.【变式训练】过抛物线y=ax2(a>0)的焦点F的直线交抛物线于
P,Q两点,若线段PF与FQ的长分别是p,q,则 等于( )【解析】选C.抛物线y=ax2的标准形式为
所以焦点 取特殊情形,
即直线PQ平行于x轴,则p=q.
如图所示,由于|PF|=|PM|,
所以 故【补偿训练】已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线
y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )【解析】选A.直线l2:x=-1为抛物线
y2=4x的准线,由抛物线的定义知,
P到l2的距离等于P到抛物线的焦点
F(1,0)的距离,故本题转化为在抛
物线y2=4x上找一个点P,使得P到点F(1,0)和直线l1的距离之
和最小,最小值为F(1,0)到直线l1:4x-3y+6=0的距离,即dmin
= 故选择A.【规范解答】抛物线的性质在求最值中的应用
【典例】(12分)已知抛物线x2=4y,点P是抛物线上的动点,点A的坐标为(12,6),求点P到点A的距离与点P到x轴的距离之和的最小值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:若在①处求错焦点坐标,导致结果出错,则本例将不得分.
失分点2:若②处不明白题意,不能充分利用抛物线的定义对距离进行转化,则会使得下一步无法解答,最多得4分.
失分点3:若不能将到x轴距离转化为到焦点距离,③处则无法利用图形判断A,P,F三点共线时,|PA|+|PF|取最小值,最多得8分.【悟题】提措施,导方向
1.定义的应用意识
涉及抛物线上点到准线的距离问题,一般考虑用点到焦点的距离进行转化,如本例中P到x轴的距离可转化为|PF|=y+1进行求解.
2.条件的合理运用
对题目给出的问题要认真分析,合理转化,如本例中求最值问题可从平面几何知识入手,利用几何意义寻找取最小值的条件.【类题试解】若抛物线C:y2=x上一点P到A(3,-1)的距离与到焦点F的距离之和最小,求点P的坐标.【解析】因为点A(3,-1)在抛物线内部,
如图所示,
设抛物线的准线为l,过抛物线上一点P,
作PQ⊥l于Q,过A作AB⊥l于B.
|PA|+|PF|=|PA|+|PQ|≥|AB|,
故当且仅当P,A,B共线时,|PF|+|PA|的值最小.
此时P点坐标为(x0,-1),代入y2=x,得x0=1.
故点P的坐标为(1,-1).
(1)抛物线是中心对称图形.( )
(2)抛物线的范围是x∈R.( )
(3)抛物线是轴对称图形.( )【解析】(1)错误.在抛物线方程中,以-x代x,-y代y,方程发生了变化,故抛物线不是中心对称图形,故此说法错误.
(2)错误.抛物线的方程不同,其范围就不一样,如y2=2px(p>0)的范围是x≥0,y∈R,故此说法错误.
(3)正确.抛物线y2=±2px(p>0)的对称轴为x轴,抛物线x2=±2py(p>0)的对称轴为y轴,故此说法正确.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)顶点在原点,对称轴为y轴且过(4,1)的抛物线方程是 .
(2)已知点(-2,3)与抛物线y2=2px(p>0)的焦点的距离是5,则p= .
(3)抛物线y=2px2(p>0)的对称轴为 .【解析】(1)由已知可设抛物线的方程为x2=ay,将点(4,1)代入,得a=16,故方程为x2=16y.
答案:x2=16y(2)y2=2px(p>0)的焦点为 由题意得
解得p=4或p=-12(舍去).
答案:4
(3)由y=2px2(p>0),得
故对称轴为y轴.
答案:y轴【要点探究】
知识点 抛物线的简单几何性质
1.抛物线的标准方程与对称性、焦点位置的关系2.抛物线的图象具有的特征
抛物线是轴对称图形,其对称轴为x轴或y轴,只有一个顶点,一个焦点,一条准线,并且离心率为1.3.在标准方程形式下抛物线的性质与椭圆、双曲线的比较【知识拓展】抛物线的通径【微思考】
(1)影响抛物线开口大小的量是什么,是如何影响的?
提示:参数p影响抛物线开口大小,p值越大,抛物线的开口越开阔,p越小,开口越扁狭.(2)点P(x0,y0)与抛物线y2=2px(p>0)的关系有哪些?分别满足什么条件?
提示:①点P(x0,y0)在抛物线y2=2px(p>0)内部?y02<2px0;
②点P(x0,y0)在抛物线y2=2px(p>0)上?y02=2px0;
③点P(x0,y0)在抛物线y2=2px(p>0)外部?y02>2px0.【即时练】
已知抛物线y2=6x,判断下列点与该抛物线的关系.
(1)P1(1, ).(2)P2(2,3).(3)P3(1,3).
【解析】将点的坐标分别代入抛物线y2=6x的方程,可知P1在
抛物线上,P2在抛物线内部,P3在抛物线外部.【题型示范】
类型一 焦半径和焦点弦问题
【典例1】
(1)过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2),若x1+x2=6,那么|AB|等于( )
A.10 B.8 C.6 D.4(2)已知抛物线y2=2px(p>0),直线l经过其焦点且与x轴垂直,并交抛物线于A,B两点,若|AB|=10,P为抛物线的准线上一点,则△ABP的面积为( )
A.20 B.25 C.30 D.50【解题探究】1.题(1)过焦点的弦问题一般如何处理?
2.题(2)中焦点到准线的距离等于多少?
【探究提示】1.过焦点的弦问题一般可转化为焦半径问题求解.
2.焦点到准线的距离等于p.【自主解答】(1)选B.由抛物线y2=4x,得p=2,
设抛物线的焦点为F,则|AB|=|AF|+|FB|=
=x1+x2+p=6+2=8.
(2)选B.因为直线l过抛物线y2=2px(p>0)的焦点且与x轴垂直,
并且交抛物线于A,B两点,则|AB|=2p=10,所以p=5,故抛物
线的方程为y2=10x,P为抛物线的准线上一点.P到直线AB的距
离为p=5,则△ABP的面积为 ×10×5=25.【方法技巧】
1.抛物线的焦半径
(1)抛物线的焦半径是指以抛物线上任意一点与抛物线焦点为
端点的线段.
(2)抛物线的焦半径公式:P(x0,y0)为抛物线上一点,F为焦点.
①若抛物线y2=2px(p>0),则|PF|=
②若抛物线y2=-2px(p>0),则|PF|=
③若抛物线x2=2py(p>0),则|PF|=
④若抛物线x2=-2py(p>0),则|PF|=2.过焦点的弦长的求解方法
设过抛物线y2=2px(p>0)的焦点的弦的端点为A(x1,y1), B(x2,y2),则|AB|=x1+x2+p,然后利用弦所在直线方程与抛物线方程联立、消元,由根与系数的关系求出x1+x2即可.【变式训练】抛物线的顶点在原点,以x轴为对称轴,经过焦点且倾斜角为135°的直线被抛物线所截得的弦长为8,试求抛物线的方程.
【解题指南】联立方程组,由过焦点的弦长公式表示出弦长,解方程求出参数值,从而得出抛物线的标准方程.【解析】若抛物线开口向右,
如图.
设抛物线的方程为y2=2px(p>0),
则直线方程为设直线交抛物线于A(x1,y1),
B(x2,y2)两点,
则由抛物线定义得|AB|=|AF|+|FB|=|AC|+|BD|
=
即x1+x2+p=8. ①
又A(x1,y1),B(x2,y2)是抛物线和直线的交点,
由 消去y,得
所以x1+x2=3p.将其代入①,得p=2.
所以所求抛物线的方程为y2=4x.
当抛物线的开口向左时,同理可求得抛物线的方程为y2=-4x.
综上,抛物线的方程为y2=4x或y2=-4x. 【补偿训练】AB是过抛物线y2=2px(p>0)焦点F的一条弦,且
|AF|=1,|BF|= 求抛物线及直线AB的方程.
【解题指南】设出A,B两点的坐标,根据抛物线定义可分别表
示出|AF|和|BF|,进而可求得|AF|+|BF|,求得x1+x2的表达
式,表示出|AF|·|BF|,建立等式求得p,则抛物线方程可得.
再由|AB|= 得sin2θ= 从而利用特殊角的三角函
数求出直线AB的斜率,由点斜式方程写出直线AB的方程.【解析】设A(x1,y1),B(x2,y2),
则|AF|= |BF|=
则|AF|+|BF|=x1+x2+p=
所以x1+x2=
因为|AF|≠|BF|,
所以过焦点 的直线斜率存在且不为0,则可设AB的方程
为又因为A,B两点是直线AB与抛物线的交点,则
所以x1·x2=
由|AF|·|BF|=
得
即 所以
抛物线方程为y2=x.设直线AB的倾斜角为θ,
又根据两点间的距离公式得|AB|2=(y2-y1)2+(x2-x1)2=(tan2θ+
1)(x2-x1)2,
由于直线AB过点
设直线AB的方程为 与抛物线方程联立得到:tan2θx2-(tan2θ+2)px+ p2tan2θ=0,
那么(x2-x1)2=(x2+x1)2-4x1x2
==4p2(tan2θ+1)×
那么|AB|2=(tan2θ+1)(x2-x1)2
=(tan2θ+1)×4p2(tan2θ+1)×所以|AB|=
由|AB|= 得
所以
所以θ=60°或120°,得
所以直线AB的方程为类型二 抛物线性质的应用
【典例2】
(1)抛物线y2=4x的焦点为F,准线为l,点A是抛物线上一点,且∠AFO=120°(O为坐标原点),AK⊥l,垂足为K,则△AKF的面积是 .
(2)已知正三角形AOB的一个顶点O位于坐标原点,另外两个顶点A,B在抛物线y2=2px(p>0)上,求这个三角形的边长.【解题探究】1.题(1)由题设条件,要求△AKF的面积,只需求出什么?
2.题(2)三角形的另两个顶点应满足什么关系?
【探究提示】1.根据题设条件,要求△AKF的面积,只需求出点A的坐标即可.
2.根据抛物线的对称性及三角形为正三角形,故A,B两点应关于x轴对称.【自主解答】(1)如图,
设A(x0,y0),
过A作AH⊥x轴于H,
在Rt△AFH中,|FH|=x0-1,
由∠AFO=120°得∠AFH=60°,
故所以点A的坐标为
将此代入抛物线方程可得3x02-10x0+3=0,
解得x0=3或x0= (舍),故S△AKF=
答案:(2)如图所示,设正三角形OAB的顶点A,B在抛物线上,且坐标分别为(x1,y1),(x2,y2),y12=2px1,y22=2px2.
又因为|OA|=|OB|,
所以x12+y12=x22+y22,
即x12-x22+2px1-2px2=0.
所以(x1-x2)(x1+x2+2p)=0.
因为x1>0,x2>0,2p>0,
所以x1+x2+2p≠0.所以x1=x2.即A,B两点关于x轴对称,则∠AOx=30°,
所以AB⊥x轴,所以y1=x1tan 30°=
又因为x1= 所以y1=
而|AB|=2y1= 即为所求边长.【延伸探究】题(2)中若△AOB为直角三角形,且∠AOB=90°,判断直线AB是否恒过定点?
【解析】直线AB恒过定点(2p,0).设
由OA⊥OB,故kOA·kOB=-1,得:
即y1·y2=-4p2.所以直线AB的方程为
即
=
将y1·y2=-4p2代入上式得
故直线AB恒过定点(2p,0).【方法技巧】利用抛物线的性质可以解决的问题
(1)对称性:解决抛物线的内接三角形问题.
(2)焦点、准线:解决与抛物线的定义有关的问题.
(3)范围:解决与抛物线有关的最值问题.
(4)焦点:解决焦点弦问题.【变式训练】已知直线l过坐标原点,
抛物线C顶点在原点,焦点在x轴正半
轴上.若点A(-1,0)和点B(0,8)关于
l的对称点都在C上,求直线l和抛物线
C的方程.【解题指南】先设出抛物线的标准方程和直线l的方程,根据A′,B′分别是A,B关于l的对称点,进而可知A′A⊥l,进而可得直线A′A的方程,把两直线方程联立求得交点M的坐标,进而根据M为AA′的中点,求得A′点的坐标和B′点的坐标,分别代入抛物线方程求得p的表达式,最后联立求得k,进而求得p,则直线和抛物线的方程可得.【解析】依题设抛物线C的方程可写为
y2=2px(p>0),
且x轴和y轴不是所求直线,又l过原点,
因而可设l的方程为y=kx(k≠0),①
设A′,B′分别是A,B关于l的对称点,因而A′A⊥l,直线
A′A的方程为 ②
由①②联立解得AA′与l的交点M的坐标为又M为AA′的中点,从而点A′的横坐标为
纵坐标为
同理得点B′的横、纵坐标分别为又A′,B′均在抛物线y2=2px(p>0)上,
由③得
由此知k≠±1,即
同理由④得 即
从而 整理得k2-k-1=0,
解得但当 时,由③知
这与点A′在抛物线y2=2px(p>0)上矛盾,故舍去
所以 则直线l的方程为
将 代入 ⑤求得
所以直线方程为 抛物线方程为【补偿训练】已知A,B是抛物线y2=2px(p>0)上两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点,求直线AB的方程.【解析】如图所示.设A(x0,y0),
由题意可知B(x0,-y0),
又 是△AOB的垂心,
则AF⊥OB,所以kAF·kOB=-1,
即 所以y02=
又y02=2px0,所以
因此直线AB的方程为类型三 抛物线中的定值与最值问题
【典例3】
(1)已知抛物线y2=2px(p>0)的经过焦点的弦AB的两端点坐标分别为A(x1,y1),B(x2,y2),则 的值一定等于( )
A.4 B.-4 C.p2 D.-p2
(2)抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐
标是( )
A.( ,1) B.(0,0) C.(1,2) D.(1,4)【解题探究】1.题(1)x1·x2可否用y1y2表示?
2.题(2)中抛物线的方程是否是标准方程,抛物线上的任意一点到直线y=4x-5的距离如何表示?【探究提示】1.能.由A,B在抛物线上,故
所以
2.已知的方程不是标准形式,可化为 可设抛物线上的
一点为(x,4x2),则其到直线的距离为【自主解答】(1)选B.由抛物线y2=2px(p>0),得焦点坐标为
设过焦点的弦AB所在直线方程为
由 消去x得:y2-2pmy-p2=0,
所以y1·y2=-p2.
由A(x1,y1),B(x2,y2)在抛物线上,故
所以(2)选A.方法一:设抛物线上点的坐标为(x,4x2),其中x∈R,
由点到直线的距离公式得
所以当 时,d最小.这时点的坐标为方法二:设与y=4x-5平行的抛物线y=4x2的切线方程为y=4x+m,
由 得4x2-4x-m=0.
再由Δ=16-4×4×(-m)=0得m=-1.
这时切点为 切点 到y=4x-5的距离最小.【方法技巧】抛物线中最值的求解策略
(1)可借助于抛物线的有关知识转化为函数的最值求解,但要注意抛物线的范围.
(2)当条件中有关于抛物线上的点P到焦点F的距离问题一定要考虑抛物线的定义,注意点P到F的距离与点P到准线距离的转化.【变式训练】过抛物线y=ax2(a>0)的焦点F的直线交抛物线于
P,Q两点,若线段PF与FQ的长分别是p,q,则 等于( )【解析】选C.抛物线y=ax2的标准形式为
所以焦点 取特殊情形,
即直线PQ平行于x轴,则p=q.
如图所示,由于|PF|=|PM|,
所以 故【补偿训练】已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线
y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )【解析】选A.直线l2:x=-1为抛物线
y2=4x的准线,由抛物线的定义知,
P到l2的距离等于P到抛物线的焦点
F(1,0)的距离,故本题转化为在抛
物线y2=4x上找一个点P,使得P到点F(1,0)和直线l1的距离之
和最小,最小值为F(1,0)到直线l1:4x-3y+6=0的距离,即dmin
= 故选择A.【规范解答】抛物线的性质在求最值中的应用
【典例】(12分)已知抛物线x2=4y,点P是抛物线上的动点,点A的坐标为(12,6),求点P到点A的距离与点P到x轴的距离之和的最小值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:若在①处求错焦点坐标,导致结果出错,则本例将不得分.
失分点2:若②处不明白题意,不能充分利用抛物线的定义对距离进行转化,则会使得下一步无法解答,最多得4分.
失分点3:若不能将到x轴距离转化为到焦点距离,③处则无法利用图形判断A,P,F三点共线时,|PA|+|PF|取最小值,最多得8分.【悟题】提措施,导方向
1.定义的应用意识
涉及抛物线上点到准线的距离问题,一般考虑用点到焦点的距离进行转化,如本例中P到x轴的距离可转化为|PF|=y+1进行求解.
2.条件的合理运用
对题目给出的问题要认真分析,合理转化,如本例中求最值问题可从平面几何知识入手,利用几何意义寻找取最小值的条件.【类题试解】若抛物线C:y2=x上一点P到A(3,-1)的距离与到焦点F的距离之和最小,求点P的坐标.【解析】因为点A(3,-1)在抛物线内部,
如图所示,
设抛物线的准线为l,过抛物线上一点P,
作PQ⊥l于Q,过A作AB⊥l于B.
|PA|+|PF|=|PA|+|PQ|≥|AB|,
故当且仅当P,A,B共线时,|PF|+|PA|的值最小.
此时P点坐标为(x0,-1),代入y2=x,得x0=1.
故点P的坐标为(1,-1).
