3.1.2 空间向量的数乘运算 课件2
文档属性
| 名称 | 3.1.2 空间向量的数乘运算 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 678.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览




文档简介
课件17张PPT。3.1.2空间向量的
数乘运算2一、共线向量:零向量与任意向量共线.1.共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作2.共线向量定理:对空间任意两个向量
的充要条件是存在实数 使3若P为A,B中点,
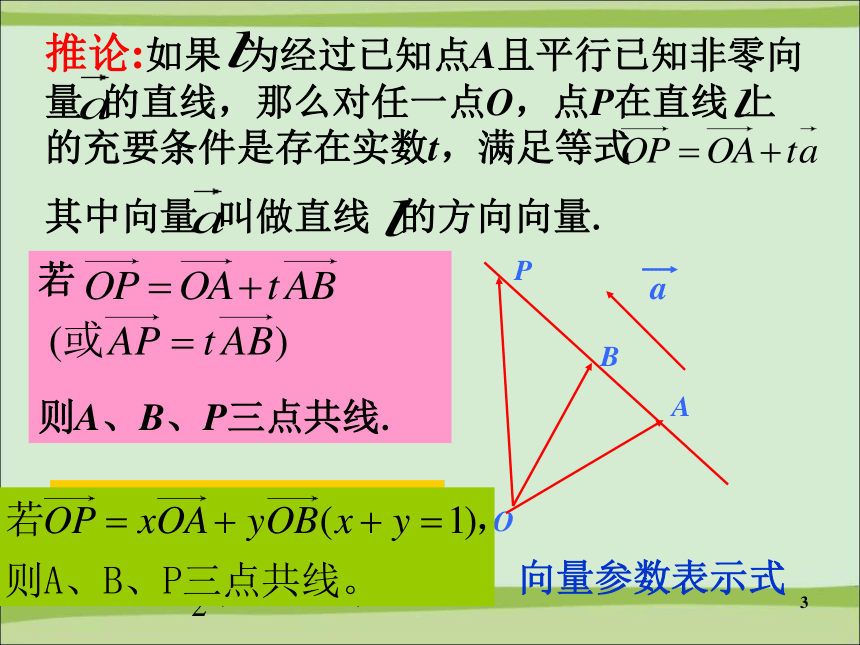
则向量参数表示式推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式
其中向量 叫做直线 的方向向量.若
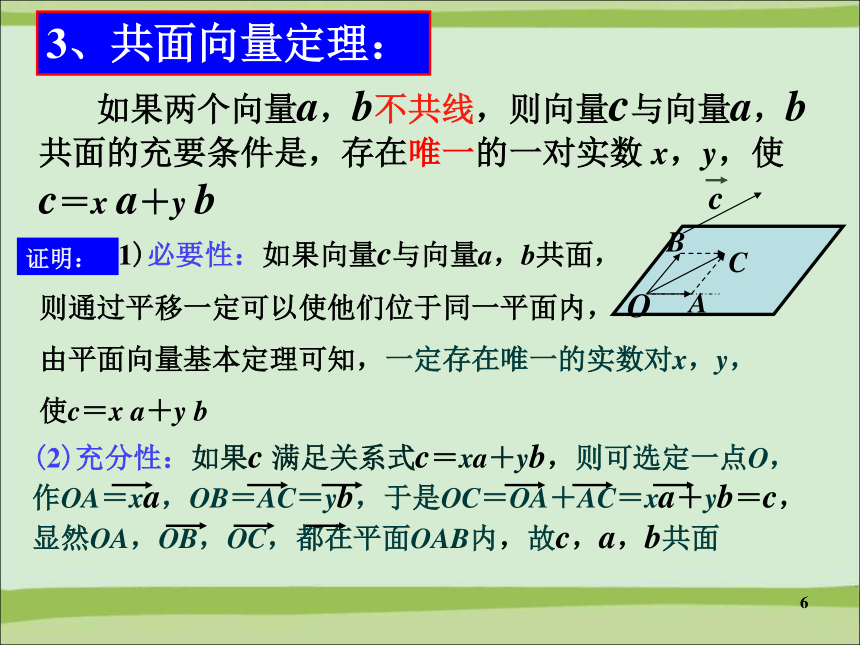
则A、B、P三点共线.3—1—2空间向量的基本定理——共面向量定理共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了.5 1、如果向量e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a与 e1, e2有什么关系? 如果e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a,存在惟一的一对实数a1,a2,使 a= a1 e1 +a2 e22、平面向量基本定理复习:6 (1)必要性:如果向量c与向量a,b共面,
则通过平移一定可以使他们位于同一平面内,
由平面向量基本定理可知,一定存在唯一的实数对x,y,
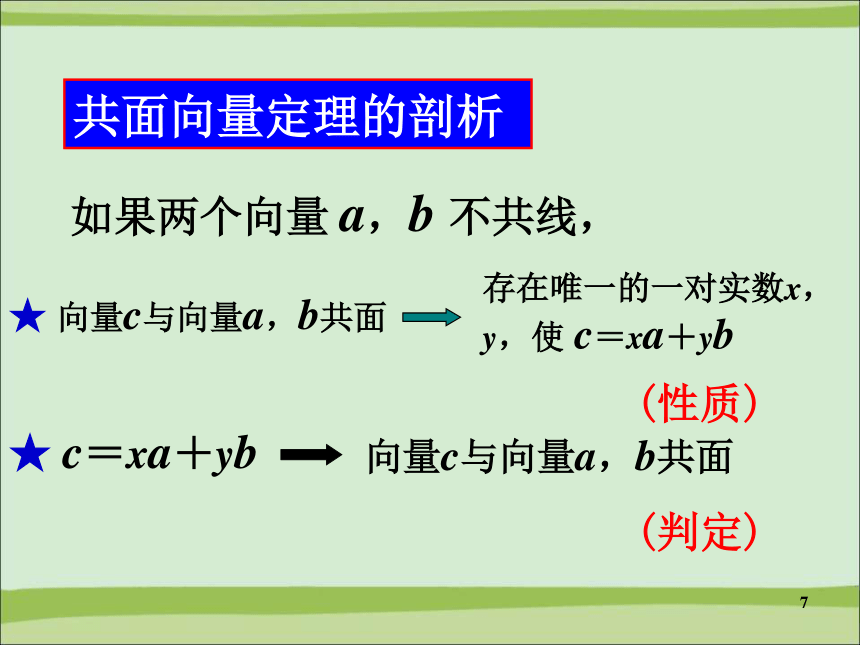
使c=x a+y b3、共面向量定理: 如果两个向量a,b不共线,则向量c与向量a,b 共面的充要条件是,存在唯一的一对实数 x,y,使 c=x a+y b证明:7共面向量定理的剖析 如果两个向量 a,b 不共线,(性质)(判定)89思考2(课本P88思考)即,P、A、B、C四点共面.10得证.11例1、已知A,B,C三点不共线,对平面ABC外的任一点O,确定在下列条件下,M是否与A,B,C三点共面:12例2(课本例)如图,已知平行四边形ABCD,从平
面AC外一点O引向量 , ,
, ,
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
13例2 (课本例)已知 ABCD ,从平面AC外一点O引向量 求证:①四点E、F、G、H共面;②平面AC//平面EG.证明:(﹡)代入所以 E、F、G、H共面.14证明:由面面平行判定定理的推论得:151.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )161.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面17变式:
求证:MN∥平面ABB’A’
数乘运算2一、共线向量:零向量与任意向量共线.1.共线向量:如果表示空间向量的有向线段所在直线互相平行或重合,则这些向量叫做共线向量(或平行向量),记作2.共线向量定理:对空间任意两个向量
的充要条件是存在实数 使3若P为A,B中点,
则向量参数表示式推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式
其中向量 叫做直线 的方向向量.若
则A、B、P三点共线.3—1—2空间向量的基本定理——共面向量定理共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了.5 1、如果向量e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a与 e1, e2有什么关系? 如果e1和e2是一平面内的两个不平行的向量,那么,该平面内的任一向量a,存在惟一的一对实数a1,a2,使 a= a1 e1 +a2 e22、平面向量基本定理复习:6 (1)必要性:如果向量c与向量a,b共面,
则通过平移一定可以使他们位于同一平面内,
由平面向量基本定理可知,一定存在唯一的实数对x,y,
使c=x a+y b3、共面向量定理: 如果两个向量a,b不共线,则向量c与向量a,b 共面的充要条件是,存在唯一的一对实数 x,y,使 c=x a+y b证明:7共面向量定理的剖析 如果两个向量 a,b 不共线,(性质)(判定)89思考2(课本P88思考)即,P、A、B、C四点共面.10得证.11例1、已知A,B,C三点不共线,对平面ABC外的任一点O,确定在下列条件下,M是否与A,B,C三点共面:12例2(课本例)如图,已知平行四边形ABCD,从平
面AC外一点O引向量 , ,
, ,
求证:
⑴四点E、F、G、H共面;
⑵平面EG//平面AC.
13例2 (课本例)已知 ABCD ,从平面AC外一点O引向量 求证:①四点E、F、G、H共面;②平面AC//平面EG.证明:(﹡)代入所以 E、F、G、H共面.14证明:由面面平行判定定理的推论得:151.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )161.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面17变式:
求证:MN∥平面ABB’A’
