3.1.2 空间向量的数乘运算 课件5
文档属性
| 名称 | 3.1.2 空间向量的数乘运算 课件5 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 18:19:00 | ||
图片预览










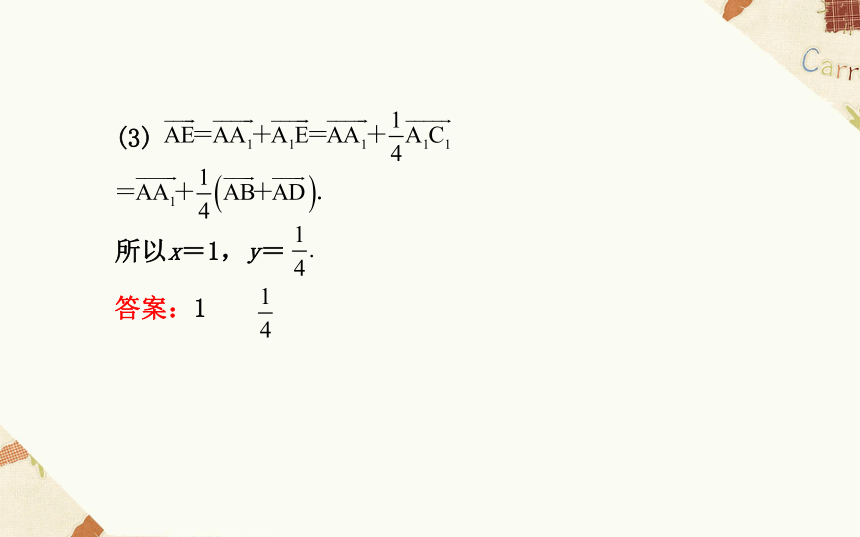
文档简介
课件74张PPT。3.1.2
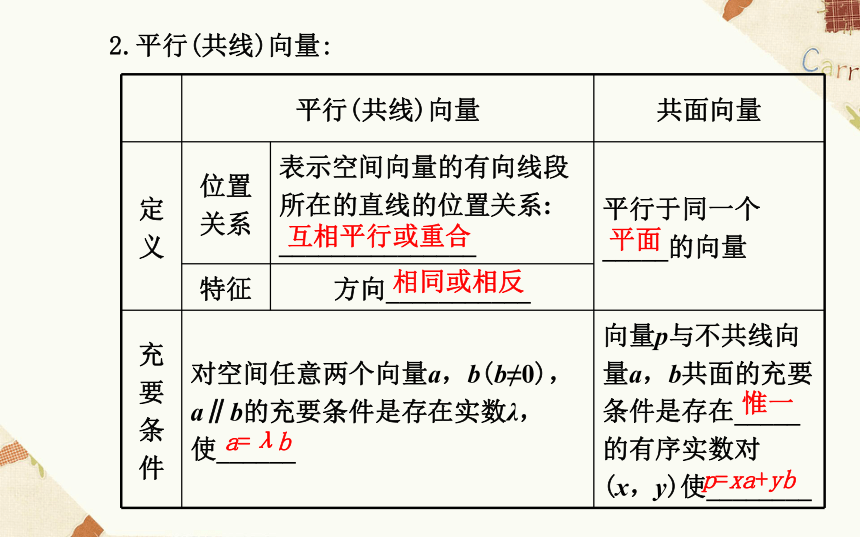
空间向量的数乘运算1.向量的数乘运算
(1)数乘运算:相同相反|λ|倍向量(2)运算律:①分配律:λ(a+b)=________;
②结合律:λ(μa)=________.λa+λb(λμ)a2.平行(共线)向量:互相平行或重合相同或相反平面a=λb惟一p=xa+yb方向向量1.判一判(正确的打“√”,错误的打“×”)
(1)实数与向量之间可进行加法、减法运算.( )
(2)若表示两向量的有向线段所在的直线为异面直线,则这
两个向量不是共面向量.( )
(3)如果 则P,A,B共线.( )
(4)空间中任意三个向量一定是共面向量.( )【解析】(1)错误,实数与向量相加没有意义,如3+a不能确定
该式子是实数还是向量.
(2)错误,由共面向量的定义知空间中任意两个向量都是共面向
量,故此种说法错误.
(3)正确,能判定P,A,B共线.因为原式可化为: 由共线
向量的充要条件可知,P,A,B共线.(4)错误,空间中的任意三个向量不一定是共
面向量.例如,对于空间四边形ABCD,
这三个向量就不是共面向量.
答案:(1)× (2)× (3)√ (4)×2.做一做(请把正确的答案写在横线上)
(1)若|a|=5,b与a的方向相反,且|b|=7,则a= b.
(2)已知b=-5a(|a|=2),向量b的长度为 ,向量b的方
向与向量a的方向 .
(3)已知正方体ABCD-A1B1C1D1中, ,若
则x= ,y= .【解析】(1)b与a的方向相反,
所以a=λb且实数λ<0,
由|a|=|λ||b|,所以 故λ=
答案:
(2)因为|a|=2,又b=-5a,
所以向量b的长度为10,
又因为-5<0,故向量b与a的方向相反.
答案:10 相反(3)
所以x=1,y=
答案:1 【要点探究】
知识点1 空间向量的数乘运算
1.数乘运算的三个关注点
(1)与实数运算的区别:数乘向量与数与数的乘法是有区别的,前者结果是一个向量,后者结果是一个实数.
(2)与加法、减法运算的关系:空间向量的数乘运算,实质是空间向量的加减运算.
(3)特殊情况:当λ=0或a=0时,向量λa=0.2.对λa的三点说明
(1)含义:λa是实数λ与向量a间的运算.
(2)λ的作用:λ的正负影响着向量λa的方向,λ的大小影响着向量λa的长度.
(3)a的作用:向量λa与向量a一定是共线向量.【知识拓展】非零向量的单位化
已知非零向量a和它的单位向量a°,显然向量|a|a°与向
量a等长且同向,所以有a=|a|a°或a°= .由此可知,一个非
零向量a除以它的模就可以得到它的单位向量.从向量a求向量
a°的过程就称为向量a的单位化.【微思考】
(1)向量λa的模与向量a的模比较何时扩大?何时缩小?
提示:向量a的模可以扩大(当|λ|>1时),也可以缩小(当|λ|<1时).
(2)向量λa的方向与向量a的方向是否一致?
提示:向量a的方向可以不改变(当λ>0时),也可以改变(当λ<0时).【即时练】
化简 (a+2b-3c)+ -3(a-2b+c)=
___________.
【解析】原式= -3a+6b-3c
答案: 知识点2 共线向量
1.对空间共线向量的两点说明
(1)类比理解:空间共线向量与平面共线向量的定义完全一样,平面共线向量的结论在空间共线向量中仍然成立.
(2)共线的理解:“共线”这个概念具有自反性,也具有对称性,即若a∥b,则b∥a.2.共线向量充要条件的三个关注点
(1)区别:共线向量与直线平行的区别,直线平行不包括两直线重合的情况,而我们说的两个共线向量a∥b,表示向量a,b的有向线段所在直线既可以是同一直线,也可以是两条平行直线.
(2)零向量:共线向量的充要条件及其推论是证明共线(平行)问题的重要依据,条件b≠0不可遗漏.
(3)方向向量的个数:直线的方向向量是指与直线平行或共线的向量.一条直线的方向向量有无限多个,它们的方向相同或相反.3.三点P,A,B共线的三种充要条件
(1)存在实数t,使得 即
(2)存在实数t,使得
(3)存在有序实数对(x,y),使得 (其中x+y=1).【知识拓展】共线向量定理推论的证明
推论:如果l为经过已知点A,且平行于已
知向量a的直线,那么对空间任一点O,点P在
直线l上的充要条件是存在实数t,满足等式 证明:因为l∥a,
所以对于l上任意一点P,存在惟一的实数t,使得 =ta.(*)
又因为对于空间任意一点O,
有
所以 ①
若在l上取AB=a,则有 (**)
又因为
所以 ②当t= 时, ③
注:其中向量a叫做直线l的方向向量.
①和②都叫空间直线的向量表示式,③是线段AB的中点向量公式.【微思考】
(1)若空间中两向量共线,则它们的方向有什么关系?
提示:两向量共线,则它们的方向相同或相反.
(2)在两向量共线的充要条件中,为什么要求b≠0?
提示:由于我们已经规定了0与任意向量平行,所以当b=0时,a与b是共线向量,可如果a≠0,就不可能存在实数λ,使a=λb成立.【即时练】
给出下列几个命题:
①若a与b共线,b与c共线,则a与c共线;
②零向量的方向是任意的;
③若a∥b,则存在惟一的实数λ,使a=λb.其中真命题的个数为 ( )
A.0 B.1 C.2 D.3【解析】选B.①错误,若b=0,则a,b共线,b,c共线,但a,c未必共线;②正确.这是关于零向量的方向的规定;③错误.若b=0,则有无数多个λ使之成立.知识点3 共面向量
1.对共面向量的两点说明
(1)共面的理解:共面向量是指与同一个平面平行的向量,可将共面向量平移到同一个平面内.
(2)向量的“自由性”:空间任意的两向量都是共面的.只要方向相同,大小相等的向量就是同一向量,只要能平移到同一平面上的向量都是共面向量.2.对共面向量充要条件的两点说明:
(1)表示式:共面向量的充要条件给出了平面的向量表示式,说
明空间中任意一个平面都可以由两个不共线的平面向量表示
出来.
(2)正反两角度:空间一点P位于平面MAB内的充分必要条件是存
在有序实数对(x,y),使 满足这个关系式的点
P都在平面MAB内;反之,平面MAB内的任一点P都满足这个关系式.
【微思考】
(1)共面向量与直线与平面平行的定义是否一样?
提示:共面向量是指表示向量的有向线段所在的直线与平面平行或表示向量的有向线段所在的直线在平面内,它与直线和平面平行是不同的.(2)在三个向量共面的充要条件中,若两向量a,b共线,那么结论是否还成立?
提示:不成立.因为当p与a,b都共线时,存在不惟一的实数对(x,y)使p=xa+yb成立.当p与a,b不共线时,不存在实数对(x,y)使p=xa+yb成立.【即时练】
以下命题:
①若a,b所在直线是异面直线,则a与b一定不共面;
②若a,b,c三向量两两共面,则a,b,c三向量一定也共面;
③若a,b,c三向量共面,则由a,b所在直线确定的平面与由b,c所在直线确定的平面一定平行或重合.其中正确命题的个数为( )
A.0个 B.1个 C.2个 D.3个【解析】选A.①错.由于向量是可以自由平移的,所以空间任意
两个向量一定共面;②错.从正方体一顶点引出的三条棱作为三
个向量,虽然是两两共面,但这三个向量不共面,三个向量共面
时,它们所在的直线或者在平面内或者与平面平行;③错.首先
a,b所在直线不一定能确定平面,其次在平行六面体ABCD-
A1B1C1D1中, 三向量共面,然而平面ABCD与平面
ABB1A1相交.
类型一 空间向量的数乘运算
【典例1】
(1)已知正方体ABCD-A′B′C′D′中,点E是A′C′的中点,点F是AE的三等分点,且AF= EF,则 等于(2)已知ABCD为正方形,P是ABCD所在平面外一点,P在平面
ABCD上的射影恰好是正方形ABCD的中心O,Q是CD的中点,
若 求式中x,y的值.【解题探究】1.题(1)中向量 如何用向量 与向量
表示? 与 关系如何?
2.题(2)中 你能确定哪些与向量
有关的三角形?
【探究提示】1.利用平行四边形法则
与 可利用线段间的长度比例关系建立联系
2.解答本题需准确画图,有关的三角形是△POQ,可得
对于△PAC可得【自主解答】(1)选D.由条件AF= EF得EF=2AF,
所以AE=AF+EF=3AF,
所以(2)如图,
因为
所以x=y=【延伸探究】在题(2)条件不变的情况下,若
求x,y的值.
【解析】因为O为AC的中点,Q为CD的中点,
所以
所以
从而有
所以x=2,y=-2.【方法技巧】利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙逆用中点坐标公式.【变式训练】已知矩形ABCD,P为平面ABCD外一点,M,N分别
为BC,PD的中点,求满足 的实数x,y,
z的值. 【解析】
所以x=-1,y=0,z=【补偿训练】已知点G是△ABC的重心,O是空间任意一点,若 求λ的值.
【解题指南】构造与向量 有关的三角形、平行四
边形,利用向量加法、减法的运算法则及数乘运算求解.【解析】连接CG并延长交AB于D,
则D为AB中点,且CG=2GD,连接AG,BG.
所以
所以λ=3.类型二 共线向量
【典例2】
(1)已知空间向量a,b且 =a+2b, =-5a+6b,=7a-2b,则一定共线的三点是( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D(2)如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且
F在对角线A1C上,且
求证:E,F,B三点共线.【解题探究】1.题(1)中 用向量a,b如何表示?
2.题(2)中的向量 与 分别用向量 表示,
其结果是什么样的?
【探究提示】1. =2a+4b.【自主解答】(1)选A. =(-5a+6b)+(7a-2b)
=2a+4b=
所以A,B,D三点共线.
(2)设
因为
所以
所以所以
又
所以 所以E,F,B三点共线.【方法技巧】
1.判断向量共线的策略
(1)熟记共线向量充要条件:①a∥b,b≠0,则存在惟一实数λ使a=λb;②若存在惟一实数λ,使a=λb,则a∥b.
(2)判断向量共线的关键:找到实数λ.2.三点共线与直线平行的判断
(1)线线平行:证明两直线平行要先证明两直线的方向向量a,
b平行,还要证明直线上有一点不在另一条直线上.
(2)三点共线:证明三点A,B,C共线,只需证明存在实数λ,
使 或 即可.【变式训练】如图所示,已知四边形ABCD,ABEF都是平行四边形
且不共面,M,N分别是AC,BF的中点,判断 与 是否共线.【解析】因为M,N分别是AC,BF的中点,
四边形ABCD,ABEF都是平行四边形,
所以
所以 即 与 共线.【补偿训练】已知A,B,C三点共线,则对空间任一点O,存在
三个不为0的实数λ,m,n,使 =0,那么λ
+m+n的值为_________.【解析】因为A,B,C三点共线,所以存在惟一实数k使
即
所以(k-1) =0,
又
令λ=k-1,m=1,n=-k,
则λ+m+n=0.
答案:0类型三 共面向量
【典例3】
(1)已知A,B,C三点不共线,O是平面ABC外任一点,若由
确定的一点P与A,B,C三点共面,
则λ=__________.(2)在长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN∶NC=2∶1,求证: 与 共面.【解题探究】1.空间一点P在平面ABC内的充要条件是存在有
序实数组(x,y,z),使得 其中x+y+z
的结果是多少?
2.题(2)中要证明 与 共面,这三个向量需建立的
关系式是什么样的?【探究提示】1.结果为1.
2.要证明 与 共面,需用其中两个向量表示另一个
向量.
【自主解答】(1)由P与A,B,C三点共面,所以 +λ=1,
解得λ=
答案: 所以
所以 与 共面.【方法技巧】
1.四点共面的证明及应用
(1)利用共面向量的充要条件:空间一点P位于平面MAB内的充
分必要条件是存在有序实数对(x,y),使
满足这个关系式的点P都在平面MAB内;反之,平面MAB内的任
一点P都满足这个关系式.这个充要条件常用以证明四点共面.(2)求参数:向量共面的充要条件的实质是共面的四点中所形成的两个不共线的向量一定可以表示其他向量,对于向量共面的充要条件,不仅会正用,也要能够逆用它求参数的值.
2.证明空间向量共面的两种方法
(1)向量表示:设法证明其中一个向量可以表示成另两个向量的线性组合,即若p=xa+yb,则向量p,a,b共面.
(2)用平面:寻找一个平面,设法证明这些向量与该平面平行.【变式训练】对于空间任一点O和不共线的三点A,B,C,有
则x+y+z=1是P,A,B,C四点共面
的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分又不必要条件【解题指南】先确定哪一部分是条件,哪一部分是结论,再
从两个方面证明看是否成立.
【解析】选B.若x+y+z=1,则
即 由共面向量充要条件可知向量
共面,所以P,A,B,C四点共面;反之,若P,A,B,C四点
共面,当O与四个点中的一个(比如A点)重合时, =0,x可
取任意值,不一定有x+y+z=1.【补偿训练】A,B,C不共线,对空间任意一点O,若
则P,A,B,C四点( )
A.不共面 B.共面
C.不一定共面 D.无法判断是否共面【解析】选B.
所以
所以
由共面的充要条件知P,A,B,C四点共面.【巧思妙解】巧用共面向量的充要条件证明共面(线面平行)
【典例】已知E,F,G,H分别是空间四边形
ABCD的边AB,BC,CD,DA的中点.
(1)证明E,F,G,H四点共面.
(2)证明BD∥平面EFGH.【教你审题】【常规解法】(1)
又
所以 所以四点E,F,G,H共面.
(2)因为
所以EH∥BD.
又EH?平面EFGH,BD?平面EFGH,
所以BD∥平面EFGH. 【巧妙解法】连接EG,BG.
(1)因为
由向量共面的充要条件知:
E,F,G,H四点共面.
(2)因为
又 不共线,所以 与 共面.
又BD?平面EFGH,所以BD∥平面EFGH.【方法对比】
常规解法切入点简单,但步骤较多,稍有疏忽,则会导致错误;巧妙解法则是直接利用共面向量的充要条件,减少了步骤,思路清晰.【教你一招】
P,A,B,C四点共面的四种充要条件
(1)存在有序实数对(x,y),使得
(2)对于空间任意一定点O,有
(3)空间一点P在平面ABC内的充要条件是存在有序实数组
(x,y,z)使得 (其中x+y+z=1).
(4)
本例的巧妙解法即是利用了第一种.【类题试解】如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和
A1D1的中点.
证明:向量 是共面向量.【常规解法】连接A1D,BD,取A1D中点G,连接FG,BG,
则有FG∥DD1,FG= DD1,
又BE∥DD1,BE= DD1,
所以FG∥BE.所以四边形BEFG为平行四边形.
所以EF∥BG.
又EF?平面A1BD,BG?平面A1BD,所以EF∥平面A1BD.
同理,B1C∥A1D,所以B1C∥平面A1BD,
所以 都与平面A1BD平行.所以 共面.【巧妙解法】
由向量共面的充要条件知, 是共面向量.
空间向量的数乘运算1.向量的数乘运算
(1)数乘运算:相同相反|λ|倍向量(2)运算律:①分配律:λ(a+b)=________;
②结合律:λ(μa)=________.λa+λb(λμ)a2.平行(共线)向量:互相平行或重合相同或相反平面a=λb惟一p=xa+yb方向向量1.判一判(正确的打“√”,错误的打“×”)
(1)实数与向量之间可进行加法、减法运算.( )
(2)若表示两向量的有向线段所在的直线为异面直线,则这
两个向量不是共面向量.( )
(3)如果 则P,A,B共线.( )
(4)空间中任意三个向量一定是共面向量.( )【解析】(1)错误,实数与向量相加没有意义,如3+a不能确定
该式子是实数还是向量.
(2)错误,由共面向量的定义知空间中任意两个向量都是共面向
量,故此种说法错误.
(3)正确,能判定P,A,B共线.因为原式可化为: 由共线
向量的充要条件可知,P,A,B共线.(4)错误,空间中的任意三个向量不一定是共
面向量.例如,对于空间四边形ABCD,
这三个向量就不是共面向量.
答案:(1)× (2)× (3)√ (4)×2.做一做(请把正确的答案写在横线上)
(1)若|a|=5,b与a的方向相反,且|b|=7,则a= b.
(2)已知b=-5a(|a|=2),向量b的长度为 ,向量b的方
向与向量a的方向 .
(3)已知正方体ABCD-A1B1C1D1中, ,若
则x= ,y= .【解析】(1)b与a的方向相反,
所以a=λb且实数λ<0,
由|a|=|λ||b|,所以 故λ=
答案:
(2)因为|a|=2,又b=-5a,
所以向量b的长度为10,
又因为-5<0,故向量b与a的方向相反.
答案:10 相反(3)
所以x=1,y=
答案:1 【要点探究】
知识点1 空间向量的数乘运算
1.数乘运算的三个关注点
(1)与实数运算的区别:数乘向量与数与数的乘法是有区别的,前者结果是一个向量,后者结果是一个实数.
(2)与加法、减法运算的关系:空间向量的数乘运算,实质是空间向量的加减运算.
(3)特殊情况:当λ=0或a=0时,向量λa=0.2.对λa的三点说明
(1)含义:λa是实数λ与向量a间的运算.
(2)λ的作用:λ的正负影响着向量λa的方向,λ的大小影响着向量λa的长度.
(3)a的作用:向量λa与向量a一定是共线向量.【知识拓展】非零向量的单位化
已知非零向量a和它的单位向量a°,显然向量|a|a°与向
量a等长且同向,所以有a=|a|a°或a°= .由此可知,一个非
零向量a除以它的模就可以得到它的单位向量.从向量a求向量
a°的过程就称为向量a的单位化.【微思考】
(1)向量λa的模与向量a的模比较何时扩大?何时缩小?
提示:向量a的模可以扩大(当|λ|>1时),也可以缩小(当|λ|<1时).
(2)向量λa的方向与向量a的方向是否一致?
提示:向量a的方向可以不改变(当λ>0时),也可以改变(当λ<0时).【即时练】
化简 (a+2b-3c)+ -3(a-2b+c)=
___________.
【解析】原式= -3a+6b-3c
答案: 知识点2 共线向量
1.对空间共线向量的两点说明
(1)类比理解:空间共线向量与平面共线向量的定义完全一样,平面共线向量的结论在空间共线向量中仍然成立.
(2)共线的理解:“共线”这个概念具有自反性,也具有对称性,即若a∥b,则b∥a.2.共线向量充要条件的三个关注点
(1)区别:共线向量与直线平行的区别,直线平行不包括两直线重合的情况,而我们说的两个共线向量a∥b,表示向量a,b的有向线段所在直线既可以是同一直线,也可以是两条平行直线.
(2)零向量:共线向量的充要条件及其推论是证明共线(平行)问题的重要依据,条件b≠0不可遗漏.
(3)方向向量的个数:直线的方向向量是指与直线平行或共线的向量.一条直线的方向向量有无限多个,它们的方向相同或相反.3.三点P,A,B共线的三种充要条件
(1)存在实数t,使得 即
(2)存在实数t,使得
(3)存在有序实数对(x,y),使得 (其中x+y=1).【知识拓展】共线向量定理推论的证明
推论:如果l为经过已知点A,且平行于已
知向量a的直线,那么对空间任一点O,点P在
直线l上的充要条件是存在实数t,满足等式 证明:因为l∥a,
所以对于l上任意一点P,存在惟一的实数t,使得 =ta.(*)
又因为对于空间任意一点O,
有
所以 ①
若在l上取AB=a,则有 (**)
又因为
所以 ②当t= 时, ③
注:其中向量a叫做直线l的方向向量.
①和②都叫空间直线的向量表示式,③是线段AB的中点向量公式.【微思考】
(1)若空间中两向量共线,则它们的方向有什么关系?
提示:两向量共线,则它们的方向相同或相反.
(2)在两向量共线的充要条件中,为什么要求b≠0?
提示:由于我们已经规定了0与任意向量平行,所以当b=0时,a与b是共线向量,可如果a≠0,就不可能存在实数λ,使a=λb成立.【即时练】
给出下列几个命题:
①若a与b共线,b与c共线,则a与c共线;
②零向量的方向是任意的;
③若a∥b,则存在惟一的实数λ,使a=λb.其中真命题的个数为 ( )
A.0 B.1 C.2 D.3【解析】选B.①错误,若b=0,则a,b共线,b,c共线,但a,c未必共线;②正确.这是关于零向量的方向的规定;③错误.若b=0,则有无数多个λ使之成立.知识点3 共面向量
1.对共面向量的两点说明
(1)共面的理解:共面向量是指与同一个平面平行的向量,可将共面向量平移到同一个平面内.
(2)向量的“自由性”:空间任意的两向量都是共面的.只要方向相同,大小相等的向量就是同一向量,只要能平移到同一平面上的向量都是共面向量.2.对共面向量充要条件的两点说明:
(1)表示式:共面向量的充要条件给出了平面的向量表示式,说
明空间中任意一个平面都可以由两个不共线的平面向量表示
出来.
(2)正反两角度:空间一点P位于平面MAB内的充分必要条件是存
在有序实数对(x,y),使 满足这个关系式的点
P都在平面MAB内;反之,平面MAB内的任一点P都满足这个关系式.
【微思考】
(1)共面向量与直线与平面平行的定义是否一样?
提示:共面向量是指表示向量的有向线段所在的直线与平面平行或表示向量的有向线段所在的直线在平面内,它与直线和平面平行是不同的.(2)在三个向量共面的充要条件中,若两向量a,b共线,那么结论是否还成立?
提示:不成立.因为当p与a,b都共线时,存在不惟一的实数对(x,y)使p=xa+yb成立.当p与a,b不共线时,不存在实数对(x,y)使p=xa+yb成立.【即时练】
以下命题:
①若a,b所在直线是异面直线,则a与b一定不共面;
②若a,b,c三向量两两共面,则a,b,c三向量一定也共面;
③若a,b,c三向量共面,则由a,b所在直线确定的平面与由b,c所在直线确定的平面一定平行或重合.其中正确命题的个数为( )
A.0个 B.1个 C.2个 D.3个【解析】选A.①错.由于向量是可以自由平移的,所以空间任意
两个向量一定共面;②错.从正方体一顶点引出的三条棱作为三
个向量,虽然是两两共面,但这三个向量不共面,三个向量共面
时,它们所在的直线或者在平面内或者与平面平行;③错.首先
a,b所在直线不一定能确定平面,其次在平行六面体ABCD-
A1B1C1D1中, 三向量共面,然而平面ABCD与平面
ABB1A1相交.
类型一 空间向量的数乘运算
【典例1】
(1)已知正方体ABCD-A′B′C′D′中,点E是A′C′的中点,点F是AE的三等分点,且AF= EF,则 等于(2)已知ABCD为正方形,P是ABCD所在平面外一点,P在平面
ABCD上的射影恰好是正方形ABCD的中心O,Q是CD的中点,
若 求式中x,y的值.【解题探究】1.题(1)中向量 如何用向量 与向量
表示? 与 关系如何?
2.题(2)中 你能确定哪些与向量
有关的三角形?
【探究提示】1.利用平行四边形法则
与 可利用线段间的长度比例关系建立联系
2.解答本题需准确画图,有关的三角形是△POQ,可得
对于△PAC可得【自主解答】(1)选D.由条件AF= EF得EF=2AF,
所以AE=AF+EF=3AF,
所以(2)如图,
因为
所以x=y=【延伸探究】在题(2)条件不变的情况下,若
求x,y的值.
【解析】因为O为AC的中点,Q为CD的中点,
所以
所以
从而有
所以x=2,y=-2.【方法技巧】利用数乘运算进行向量表示的技巧
(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.
(2)明确目标:在化简过程中要有目标意识,巧妙逆用中点坐标公式.【变式训练】已知矩形ABCD,P为平面ABCD外一点,M,N分别
为BC,PD的中点,求满足 的实数x,y,
z的值. 【解析】
所以x=-1,y=0,z=【补偿训练】已知点G是△ABC的重心,O是空间任意一点,若 求λ的值.
【解题指南】构造与向量 有关的三角形、平行四
边形,利用向量加法、减法的运算法则及数乘运算求解.【解析】连接CG并延长交AB于D,
则D为AB中点,且CG=2GD,连接AG,BG.
所以
所以λ=3.类型二 共线向量
【典例2】
(1)已知空间向量a,b且 =a+2b, =-5a+6b,=7a-2b,则一定共线的三点是( )
A.A,B,D B.A,B,C
C.B,C,D D.A,C,D(2)如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且
F在对角线A1C上,且
求证:E,F,B三点共线.【解题探究】1.题(1)中 用向量a,b如何表示?
2.题(2)中的向量 与 分别用向量 表示,
其结果是什么样的?
【探究提示】1. =2a+4b.【自主解答】(1)选A. =(-5a+6b)+(7a-2b)
=2a+4b=
所以A,B,D三点共线.
(2)设
因为
所以
所以所以
又
所以 所以E,F,B三点共线.【方法技巧】
1.判断向量共线的策略
(1)熟记共线向量充要条件:①a∥b,b≠0,则存在惟一实数λ使a=λb;②若存在惟一实数λ,使a=λb,则a∥b.
(2)判断向量共线的关键:找到实数λ.2.三点共线与直线平行的判断
(1)线线平行:证明两直线平行要先证明两直线的方向向量a,
b平行,还要证明直线上有一点不在另一条直线上.
(2)三点共线:证明三点A,B,C共线,只需证明存在实数λ,
使 或 即可.【变式训练】如图所示,已知四边形ABCD,ABEF都是平行四边形
且不共面,M,N分别是AC,BF的中点,判断 与 是否共线.【解析】因为M,N分别是AC,BF的中点,
四边形ABCD,ABEF都是平行四边形,
所以
所以 即 与 共线.【补偿训练】已知A,B,C三点共线,则对空间任一点O,存在
三个不为0的实数λ,m,n,使 =0,那么λ
+m+n的值为_________.【解析】因为A,B,C三点共线,所以存在惟一实数k使
即
所以(k-1) =0,
又
令λ=k-1,m=1,n=-k,
则λ+m+n=0.
答案:0类型三 共面向量
【典例3】
(1)已知A,B,C三点不共线,O是平面ABC外任一点,若由
确定的一点P与A,B,C三点共面,
则λ=__________.(2)在长方体ABCD-A1B1C1D1中,M为DD1的中点,N在AC上,且AN∶NC=2∶1,求证: 与 共面.【解题探究】1.空间一点P在平面ABC内的充要条件是存在有
序实数组(x,y,z),使得 其中x+y+z
的结果是多少?
2.题(2)中要证明 与 共面,这三个向量需建立的
关系式是什么样的?【探究提示】1.结果为1.
2.要证明 与 共面,需用其中两个向量表示另一个
向量.
【自主解答】(1)由P与A,B,C三点共面,所以 +λ=1,
解得λ=
答案: 所以
所以 与 共面.【方法技巧】
1.四点共面的证明及应用
(1)利用共面向量的充要条件:空间一点P位于平面MAB内的充
分必要条件是存在有序实数对(x,y),使
满足这个关系式的点P都在平面MAB内;反之,平面MAB内的任
一点P都满足这个关系式.这个充要条件常用以证明四点共面.(2)求参数:向量共面的充要条件的实质是共面的四点中所形成的两个不共线的向量一定可以表示其他向量,对于向量共面的充要条件,不仅会正用,也要能够逆用它求参数的值.
2.证明空间向量共面的两种方法
(1)向量表示:设法证明其中一个向量可以表示成另两个向量的线性组合,即若p=xa+yb,则向量p,a,b共面.
(2)用平面:寻找一个平面,设法证明这些向量与该平面平行.【变式训练】对于空间任一点O和不共线的三点A,B,C,有
则x+y+z=1是P,A,B,C四点共面
的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分又不必要条件【解题指南】先确定哪一部分是条件,哪一部分是结论,再
从两个方面证明看是否成立.
【解析】选B.若x+y+z=1,则
即 由共面向量充要条件可知向量
共面,所以P,A,B,C四点共面;反之,若P,A,B,C四点
共面,当O与四个点中的一个(比如A点)重合时, =0,x可
取任意值,不一定有x+y+z=1.【补偿训练】A,B,C不共线,对空间任意一点O,若
则P,A,B,C四点( )
A.不共面 B.共面
C.不一定共面 D.无法判断是否共面【解析】选B.
所以
所以
由共面的充要条件知P,A,B,C四点共面.【巧思妙解】巧用共面向量的充要条件证明共面(线面平行)
【典例】已知E,F,G,H分别是空间四边形
ABCD的边AB,BC,CD,DA的中点.
(1)证明E,F,G,H四点共面.
(2)证明BD∥平面EFGH.【教你审题】【常规解法】(1)
又
所以 所以四点E,F,G,H共面.
(2)因为
所以EH∥BD.
又EH?平面EFGH,BD?平面EFGH,
所以BD∥平面EFGH. 【巧妙解法】连接EG,BG.
(1)因为
由向量共面的充要条件知:
E,F,G,H四点共面.
(2)因为
又 不共线,所以 与 共面.
又BD?平面EFGH,所以BD∥平面EFGH.【方法对比】
常规解法切入点简单,但步骤较多,稍有疏忽,则会导致错误;巧妙解法则是直接利用共面向量的充要条件,减少了步骤,思路清晰.【教你一招】
P,A,B,C四点共面的四种充要条件
(1)存在有序实数对(x,y),使得
(2)对于空间任意一定点O,有
(3)空间一点P在平面ABC内的充要条件是存在有序实数组
(x,y,z)使得 (其中x+y+z=1).
(4)
本例的巧妙解法即是利用了第一种.【类题试解】如图,正方体ABCD-A1B1C1D1中,E,F分别为BB1和
A1D1的中点.
证明:向量 是共面向量.【常规解法】连接A1D,BD,取A1D中点G,连接FG,BG,
则有FG∥DD1,FG= DD1,
又BE∥DD1,BE= DD1,
所以FG∥BE.所以四边形BEFG为平行四边形.
所以EF∥BG.
又EF?平面A1BD,BG?平面A1BD,所以EF∥平面A1BD.
同理,B1C∥A1D,所以B1C∥平面A1BD,
所以 都与平面A1BD平行.所以 共面.【巧妙解法】
由向量共面的充要条件知, 是共面向量.
