3.1.3 空间向量的数量积运算 课件4
文档属性
| 名称 | 3.1.3 空间向量的数量积运算 课件4 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 18:25:16 | ||
图片预览










文档简介
课件72张PPT。3.1.3
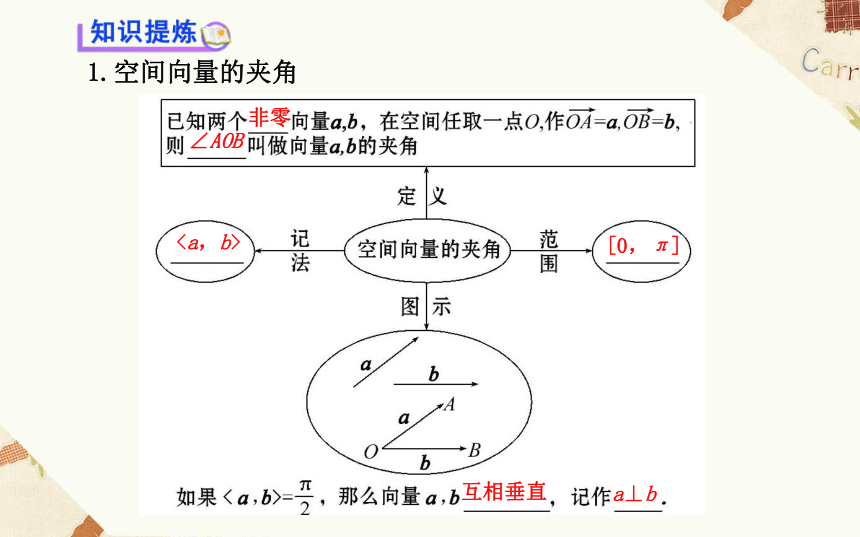
空间向量的数量积运算1.空间向量的夹角非零∠AOB[0,π]互相垂直a⊥b2.空间向量的数量积
(1)定义:已知两个非零向量a,b,则_______________叫做a与b
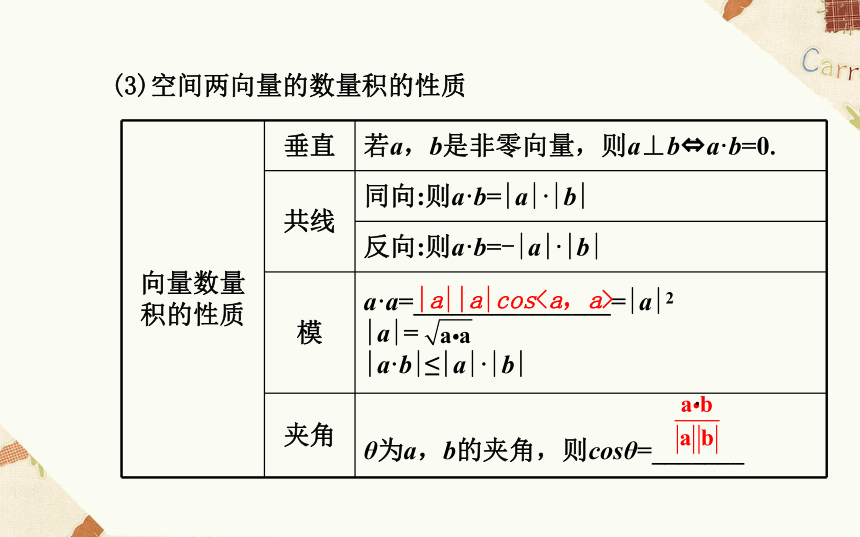
的数量积,记作a·b.即a·b=_______________.|a||b|cos|a||b|cos(2)数量积的运算律:a·bλbb·aa·b+a·c(3)空间两向量的数量积的性质|a||a|cos··1.判一判(正确的打“√”,错误的打“×”)
(1)若a·b=0,则a=0或b=0.( )
(2)与(a,b)都表示直角坐标系下的点.( )
(3)若a,b均为非零向量,则a·b=|a||b|是a与b共线的充要条
件.( )
(4)在△ABC中,< >=∠B.( )【解析】(1)错误.当两非零向量a,b的夹角为90°时,其数量积为0.
(2)错误.表示的是空间向量a,b之间的夹角,(a,b)表示直角坐标系下的点.
(3)错误.因a,b均为非零向量,故a·b=|a||b|cos =|a||b|,所以cos=1,故向量a,b共线,反之当a,b共线时,a·b=|a||b|cos=±|a||b|,故错误.(4)错误.在△ABC中,向量 的夹角为∠B,而向量
的夹角与向量 的夹角互补,故此等式不正确.
答案:(1)× (2)× (3)× (4)×2.做一做(请把正确的答案写在横线上)
(1)若向量a与b满足|a|=1,|b|=2且a与b的夹角为 ,则
a·b= .
(2)已知|a|= ,|b|= ,a·b=- ,则a与b的夹角为 .
(3)已知a,b是空间两个向量,若|a|=2,|b|=2,|a-b|= ,
则cos= .【解析】(1)a·b=|a||b|cos〈a,b〉=1×2× =1.
答案:1
(2)由a·b=|a||b|cos〈a,b〉= ×cos〈a,b〉
得cos〈a,b〉= 故a与b的夹角为135°.
答案:135°
(3)将|a-b|= 化为(a-b)2=7,求得a·b= 再由a·b
=|a||b|cos〈a,b〉求得cos〈a,b〉=
答案: 【要点探究】
知识点1 空间向量的夹角
1.空间向量夹角的两个关注点
(1)作图:共起点,作空间两个向量夹角时把两个向量起点放在一起.
(2)非负性:两向量夹角为从同一个顶点出发的两个向量所构成的较小的非负角.2.空间向量的夹角与向量位置关系
(1)=0时,向量a,b方向相同.
(2)=π时,向量a,b方向相反.
(3)= 时,向量a⊥b.【微思考】
(1)与相等吗?若两个非零向量垂直,两向量对应夹
角是多少?
提示:与分别表示向量a,b与b,a的夹角,根据空间向
量夹角的定义,与相等,若两个非零向量垂直,两向
量对应的夹角是 .(2)说出式子 表示的含义,并指出
它们之间有什么关系?
提示: 表示向量 的夹角;
表示向量 的夹角.
相互关系为【即时练】
空间四面体O-ABC中,OB=OC,∠AOB=∠AOC= 则
的值是( )
【解析】选D. ·知识点2 空间向量的数量积
1.对空间向量的数量积的三点说明
(1)运算结果:空间向量数量积的结果是个实数,而不是向量,它的值为两向量的模与两向量夹角的余弦值的乘积.
(2)运算符“·”:其中a·b中的圆点是数量积运算的符号,不能省略也不能用“×”代替.(3)注意点:①数量积的符号由夹角的余弦值决定.
②数量积不满足结合律,即(a·b)·c≠a·(b·c).
③当a≠0时由a·b=0可得a⊥b或b=0.
④空间向量没有除法运算:即若a·b=k,则没有a= .2.对空间向量数量积性质的三点说明
(1)向量模的应用:
|a|= :该式子可以解决有关空间长度问题.
(2)向量夹角的应用:空间中两条直线(特别是两条异面直线)
的夹角,可以通过求出这两个向量的夹角而求得.
(3)数量积的应用:两非零向量a,b,若a·b=0则两向量对应的直
线相互垂直.·【知识拓展】空间向量数量积的几何意义
类比平面向量投影的概念,借助图形,叙述作出向量 在轴l上
投影(空间中称为射影)的过程.已知图中向量 =a,l为轴,向量e是l上与l轴同方向的单位向量,
作点A在l上的射影A′,作点B在l上的射影B′,则 称为向量
在轴l上或在e的方向上的正射影;可以证明A′B′=
| |cos=a·e.
注意:轴l上的正射影 对应的数值A′B′是一个可正可负
可零的实数,它的符号代表向量 与l的方向的相对关系,大小
代表在l上射影的长度.【微思考】
(1)利用数量积怎样证明两个向量垂直?
提示:要证明两个非零向量垂直,即= ,只需证明a·b=0
即可.
(2)两向量运算满足多项式的运算法则吗?
提示:两向量运算满足多项式的运算法则,如常见的数量积运
算(a+b)(a-b)=a2-b2,
(a±b)2=(a±b)(a±b)=a2±2a·b+b2.【即时练】
若a,b,c为任意向量,下列命题是真命题的是( )
A.若|a|=|b|,则a=b
B.若a·b=a·c,则b=c
C.(a·b)·c=a·(b·c)=(a·c)·b
D.若|a|= |b|,且a,b夹角为45°,则(a-b)⊥b【解析】选D.对于A,模相等的向量不一定是相等向量,不成立;
对于B,当a=0时,则不一定成立;对于C,因为a·b,b·c,a·c仅
表示实数所以不成立;对于D,因(a-b)·b=a·b-b2= |a|·|b|cos45°-|b|2=0,故成立.【题型示范】
类型一 数量积的计算
【典例1】
(1)已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD, PB,PC,PD,则下列各组向量中,数量积不为零的是( )(2)已知长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AA1B1B的中心,F为A1D1的中点.求下列向量的数量积:··【解题探究】1.题(1)观察图形中直线PC与直线BD,直线DA与
直线PB,直线PD与直线AB,直线PA与直线CD是否垂直?
2.题(2)中长方体中向量 用向量 如何表示?
【探究提示】1.因直线BD与AC是否垂直不确定,故直线PC与
直线BD不一定垂直,DA与PB垂直,PD与AB垂直,PA与CD垂直.
2. 【自主解答】(1)选A.由图分析可知,选项B,C,D中两向量的
夹角均为90°,所以数量积都为0.
(2)如图所示,设 =a, =b, =c,
则|a|=|c|=2,|b|=4,
a·b=b·c=c·a=0.
①
=|b|2=42=16.
② ·
= =|c|2-|a|2=22-22=0.······【延伸探究】若题(2)的条件不变,结论改为计算
则结果如何?
【解析】····【方法技巧】
1.空间向量运算的两种方法
(1)利用定义:利用a·b=|a||b|cos〈a,b〉并结合运算律进行计算.
(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.2.在几何体中求空间向量数量积的步骤
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入a·b=|a||b|cos〈a,b〉求解.【变式训练】已知正方体ABCD-A1B1C1D1(棱长为1),A1C1∩B1D1=O,
求 ·【解析】所以········【补偿训练】已知正方体ABCD-A1B1C1D1的棱长为a,则
= .
【解析】连接向量,
= a× a×cos60°=a2.
答案:a2·····类型二 利用数量积求夹角或模
【典例2】
(1)已知空间四面体OABC各边及对角线
长都相等,E,F分别为AB,OC的中点,则向量 与向量 所成
角的余弦值为 .(2)在如图平行四边形ABCD中,| |=4,| |=3,∠D=
60°,PA⊥平面ABCD,| |=6,则向量 的模为多少?【解题探究】1.题(1)中 可用哪些向量表示?
的模怎么求?
2.题(2)中向量 模长的计算公式是什么?
【探究提示】1.用 表示向量 借助正三角
形△OAB,△BOC求 与 的模.
2. 【自主解答】(1)设 =a, =b,
=c且|a|=|b|=|c|=1,
易知∠AOB=∠BOC=∠AOC=
则a·b=b·c=c·a=
因为 = (a+b),所以
设 与 所成的角为θ,
所以向量 与向量 所成角的余弦值为
答案: ·······(2)因为
所以
所以| |=7.···【延伸探究】若把题(1)中的结论“向量 与向量 所成角
的余弦值”改为“求异面直线OE与BF所成角的余弦值”结果
如何?
【解析】如上题(1)所求设 与 所成的角为θ,
又因异面直线所成角为锐角或直角,
所以OE与BF所成角的余弦值为··【方法技巧】两个非零向量夹角求法的两个途径
(1)转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解.(2)利用数量积求夹角的余弦值【变式训练】如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD′=30°,AB=a,AC=BD=b,求CD的长.【解析】由AC⊥α,可知AC⊥AB.由∠DBD′=30°,
可知〈 〉=60°,所以
=b2+a2+b2+2(0+b2cos 60°+0)=a2+3b2,
所以 即CD=····【补偿训练】如图,在正方体ABCD-A1B1C1D1中,求 与 夹角
的大小.【解析】不妨设正方体的棱长为1,
又因为
所以
因为0°≤〈 〉≤180°,
所以〈 〉=60°.
所以 与 夹角的大小为60°.·······类型三 利用数量积解决垂直问题
【典例3】
(1)已知向量a,b是平面α内的两个不相等的非零向量,非零向量c是直线l的一个方向向量,则c·a=0且c·b=0是l⊥α的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件(2)已知在空间四面体OACB中,OB=OC,AB=AC,求证:OA⊥BC.【解题探究】1.题(1)中向量a,b是否共线,要证线面垂直,
需满足的条件有哪些?
2.题(2)中向量 能否用向量 表示?若要用向量证明
直线OA⊥BC,需证明的结论是什么?
【探究提示】1.不能确定向量a,b是否共线,需要进行讨论,
要证线面垂直,需满足的条件有直线与平面内的两条相交直
线垂直.
2. 需证明的结论是 =0.·【自主解答】(1)选B.当a与b不共线时,由c·a=0,c·b=0,可推出l⊥α;当a与b为共线向量时,由c·a=0,c·b=0,不能够推出l⊥α;l⊥α一定有c·a=0且c·b=0.
(2)因为OB=OC,AB=AC,OA=OA,
所以△OAC≌△OAB.所以∠AOC=∠AOB.
因为
所以 所以OA⊥BC.····【方法技巧】利用空间向量解决垂直问题的方法
(1)证明线线垂直的方法
证明线线垂直关键是确定直线的方向向量,看方向向量的数量积是否为0判断两直线是否垂直.
(2)证明与空间向量a,b,c有关的向量m,n垂直的方法.
先用向量a,b,c表示向量m,n,再求解向量m,n的数量积判断是否为0.【变式训练】已知|a|= |b|=4,m=a+b,n=a+λb,
〈a,b〉=135°,m⊥n,则λ=________.
【解题指南】利用m⊥n可得m·n=0进而建立与向量a,b有关
的等量关系,利用等量关系求字母的值.【解析】由m⊥n,得(a+b)·(a+λb)=0,
所以a2+(1+λ)a·b+λb2=0,
所以18+(λ+1)× ×4cos 135°+16λ=0,
即4λ+6=0,所以λ=
答案: 【补偿训练】如图,已知△ABC在平面α内,∠A=90°,DA⊥平面α,则直线CA与DB的位置关系是______.【解题指南】先找出与CA,DB对应的空间向量,再利用向量
间的关系判断两直线的位置关系.
【解析】因为
所以CA⊥DB.
答案:垂直····【拓展类型】数量积的应用
【备选例题】(1)设A,B,C,D是空间
不共面的四点,且满足
则△BCD是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.不确定···(2)如图所示,如果直线AB与平面α交于点B,且与平面α内的经过点B的三条直线BC,BD,BE所成的角相等.求证:AB⊥平面α.【解析】(1)选B.如图所示,
设
所以 =(a-b)·(c-b)
=a·c-b·c-a·b+b2=b2>0.
同理
所以△BCD的各内角均为锐角,即△BCD为锐角三角形.···(2)在直线BC,BD,BE上取
因为 与 所成的角相等,
所以
所以·····即
所以AB⊥DC,AB⊥DE.
又DC∩DE=D,
所以AB⊥平面α.··【方法技巧】
1.判断三角形的形状
利用数量积的符号可以判断两向量夹角是钝角、锐角还是直角,进而能够判断对应三角形的形状.
2.证明垂直
利用两向量数量积是否等于0,判断两向量是否垂直,进而可判断与垂直有关的几何问题.【规范解答】利用向量的数量积求异面直线所成的角
【典例】(12分)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,
AB=BC=1,AA1= ,求异面直线BA1与AC所成角的余弦值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时若忽视条件∠ABC=90°,即得不出①处的
结论,则本例基本不得分.
失分点2:解题时若忽视直三棱柱的条件,则不能得出②处结
论 则实际的考试中最多得2分.
失分点3:解题时若忽视异面直线所成角的范围,导致③处结
果写为 则实际的考试中至少会扣掉2分.··【悟题】提措施,导方向
1.关注两种意识
(1)范围意识:对于异面直线所成角,要注意其所成角的范围
为 余弦值的范围为[0,1).
(2)转化意识:把异面直线所成角与直线方向向量所成角进行
合理转化.2.关注向量表示
在运用向量进行计算时注意,找部分夹角特殊,长度特殊的向
量用这样的向量表示直线的方向向量,如本例中用
表示所求解的向量.
3.利用向量法求两异面直线的夹角的关注点
利用向量的数量积求出两向量的夹角,则这个夹角就是两异面
直线所成的角或者是其补角(注意异面直线所成角的范围).如
本例中两异面直线所成角的余弦值为正数,而非负数.【类题试解】已知在正方体中,M,N分别为棱BC和棱CC1的中点,求异面直线AC和MN所成的角.【解析】设正方体的棱长为2.
所以
又 即
所以
所以〈 〉=60°,
即异面直线AC和MN所成的角为60°.········
空间向量的数量积运算1.空间向量的夹角非零∠AOB
(1)定义:已知两个非零向量a,b,则_______________叫做a与b
的数量积,记作a·b.即a·b=_______________.|a||b|cos
(1)若a·b=0,则a=0或b=0.( )
(2)
(3)若a,b均为非零向量,则a·b=|a||b|是a与b共线的充要条
件.( )
(4)在△ABC中,< >=∠B.( )【解析】(1)错误.当两非零向量a,b的夹角为90°时,其数量积为0.
(2)错误.
(3)错误.因a,b均为非零向量,故a·b=|a||b|cos
的夹角与向量 的夹角互补,故此等式不正确.
答案:(1)× (2)× (3)× (4)×2.做一做(请把正确的答案写在横线上)
(1)若向量a与b满足|a|=1,|b|=2且a与b的夹角为 ,则
a·b= .
(2)已知|a|= ,|b|= ,a·b=- ,则a与b的夹角为 .
(3)已知a,b是空间两个向量,若|a|=2,|b|=2,|a-b|= ,
则cos
答案:1
(2)由a·b=|a||b|cos〈a,b〉= ×cos〈a,b〉
得cos〈a,b〉= 故a与b的夹角为135°.
答案:135°
(3)将|a-b|= 化为(a-b)2=7,求得a·b= 再由a·b
=|a||b|cos〈a,b〉求得cos〈a,b〉=
答案: 【要点探究】
知识点1 空间向量的夹角
1.空间向量夹角的两个关注点
(1)作图:共起点,作空间两个向量夹角时把两个向量起点放在一起.
(2)非负性:两向量夹角为从同一个顶点出发的两个向量所构成的较小的非负角.2.空间向量的夹角与向量位置关系
(1)
(2)
(3)
(1)
角是多少?
提示:
量夹角的定义,
量对应的夹角是 .(2)说出式子 表示的含义,并指出
它们之间有什么关系?
提示: 表示向量 的夹角;
表示向量 的夹角.
相互关系为【即时练】
空间四面体O-ABC中,OB=OC,∠AOB=∠AOC= 则
的值是( )
【解析】选D. ·知识点2 空间向量的数量积
1.对空间向量的数量积的三点说明
(1)运算结果:空间向量数量积的结果是个实数,而不是向量,它的值为两向量的模与两向量夹角的余弦值的乘积.
(2)运算符“·”:其中a·b中的圆点是数量积运算的符号,不能省略也不能用“×”代替.(3)注意点:①数量积的符号由夹角的余弦值决定.
②数量积不满足结合律,即(a·b)·c≠a·(b·c).
③当a≠0时由a·b=0可得a⊥b或b=0.
④空间向量没有除法运算:即若a·b=k,则没有a= .2.对空间向量数量积性质的三点说明
(1)向量模的应用:
|a|= :该式子可以解决有关空间长度问题.
(2)向量夹角的应用:空间中两条直线(特别是两条异面直线)
的夹角,可以通过求出这两个向量的夹角而求得.
(3)数量积的应用:两非零向量a,b,若a·b=0则两向量对应的直
线相互垂直.·【知识拓展】空间向量数量积的几何意义
类比平面向量投影的概念,借助图形,叙述作出向量 在轴l上
投影(空间中称为射影)的过程.已知图中向量 =a,l为轴,向量e是l上与l轴同方向的单位向量,
作点A在l上的射影A′,作点B在l上的射影B′,则 称为向量
在轴l上或在e的方向上的正射影;可以证明A′B′=
| |cos
注意:轴l上的正射影 对应的数值A′B′是一个可正可负
可零的实数,它的符号代表向量 与l的方向的相对关系,大小
代表在l上射影的长度.【微思考】
(1)利用数量积怎样证明两个向量垂直?
提示:要证明两个非零向量垂直,即
即可.
(2)两向量运算满足多项式的运算法则吗?
提示:两向量运算满足多项式的运算法则,如常见的数量积运
算(a+b)(a-b)=a2-b2,
(a±b)2=(a±b)(a±b)=a2±2a·b+b2.【即时练】
若a,b,c为任意向量,下列命题是真命题的是( )
A.若|a|=|b|,则a=b
B.若a·b=a·c,则b=c
C.(a·b)·c=a·(b·c)=(a·c)·b
D.若|a|= |b|,且a,b夹角为45°,则(a-b)⊥b【解析】选D.对于A,模相等的向量不一定是相等向量,不成立;
对于B,当a=0时,则不一定成立;对于C,因为a·b,b·c,a·c仅
表示实数所以不成立;对于D,因(a-b)·b=a·b-b2= |a|·|b|cos45°-|b|2=0,故成立.【题型示范】
类型一 数量积的计算
【典例1】
(1)已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD, PB,PC,PD,则下列各组向量中,数量积不为零的是( )(2)已知长方体ABCD-A1B1C1D1中,AB=AA1=2,AD=4,E为侧面AA1B1B的中心,F为A1D1的中点.求下列向量的数量积:··【解题探究】1.题(1)观察图形中直线PC与直线BD,直线DA与
直线PB,直线PD与直线AB,直线PA与直线CD是否垂直?
2.题(2)中长方体中向量 用向量 如何表示?
【探究提示】1.因直线BD与AC是否垂直不确定,故直线PC与
直线BD不一定垂直,DA与PB垂直,PD与AB垂直,PA与CD垂直.
2. 【自主解答】(1)选A.由图分析可知,选项B,C,D中两向量的
夹角均为90°,所以数量积都为0.
(2)如图所示,设 =a, =b, =c,
则|a|=|c|=2,|b|=4,
a·b=b·c=c·a=0.
①
=|b|2=42=16.
② ·
= =|c|2-|a|2=22-22=0.······【延伸探究】若题(2)的条件不变,结论改为计算
则结果如何?
【解析】····【方法技巧】
1.空间向量运算的两种方法
(1)利用定义:利用a·b=|a||b|cos〈a,b〉并结合运算律进行计算.
(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.2.在几何体中求空间向量数量积的步骤
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入a·b=|a||b|cos〈a,b〉求解.【变式训练】已知正方体ABCD-A1B1C1D1(棱长为1),A1C1∩B1D1=O,
求 ·【解析】所以········【补偿训练】已知正方体ABCD-A1B1C1D1的棱长为a,则
= .
【解析】连接向量,
= a× a×cos60°=a2.
答案:a2·····类型二 利用数量积求夹角或模
【典例2】
(1)已知空间四面体OABC各边及对角线
长都相等,E,F分别为AB,OC的中点,则向量 与向量 所成
角的余弦值为 .(2)在如图平行四边形ABCD中,| |=4,| |=3,∠D=
60°,PA⊥平面ABCD,| |=6,则向量 的模为多少?【解题探究】1.题(1)中 可用哪些向量表示?
的模怎么求?
2.题(2)中向量 模长的计算公式是什么?
【探究提示】1.用 表示向量 借助正三角
形△OAB,△BOC求 与 的模.
2. 【自主解答】(1)设 =a, =b,
=c且|a|=|b|=|c|=1,
易知∠AOB=∠BOC=∠AOC=
则a·b=b·c=c·a=
因为 = (a+b),所以
设 与 所成的角为θ,
所以向量 与向量 所成角的余弦值为
答案: ·······(2)因为
所以
所以| |=7.···【延伸探究】若把题(1)中的结论“向量 与向量 所成角
的余弦值”改为“求异面直线OE与BF所成角的余弦值”结果
如何?
【解析】如上题(1)所求设 与 所成的角为θ,
又因异面直线所成角为锐角或直角,
所以OE与BF所成角的余弦值为··【方法技巧】两个非零向量夹角求法的两个途径
(1)转化求角:把向量夹角转化为平面几何中的对应角,利用解三角形的知识求解.(2)利用数量积求夹角的余弦值【变式训练】如图所示,已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,线段DD′⊥α于D′,如果∠DBD′=30°,AB=a,AC=BD=b,求CD的长.【解析】由AC⊥α,可知AC⊥AB.由∠DBD′=30°,
可知〈 〉=60°,所以
=b2+a2+b2+2(0+b2cos 60°+0)=a2+3b2,
所以 即CD=····【补偿训练】如图,在正方体ABCD-A1B1C1D1中,求 与 夹角
的大小.【解析】不妨设正方体的棱长为1,
又因为
所以
因为0°≤〈 〉≤180°,
所以〈 〉=60°.
所以 与 夹角的大小为60°.·······类型三 利用数量积解决垂直问题
【典例3】
(1)已知向量a,b是平面α内的两个不相等的非零向量,非零向量c是直线l的一个方向向量,则c·a=0且c·b=0是l⊥α的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件(2)已知在空间四面体OACB中,OB=OC,AB=AC,求证:OA⊥BC.【解题探究】1.题(1)中向量a,b是否共线,要证线面垂直,
需满足的条件有哪些?
2.题(2)中向量 能否用向量 表示?若要用向量证明
直线OA⊥BC,需证明的结论是什么?
【探究提示】1.不能确定向量a,b是否共线,需要进行讨论,
要证线面垂直,需满足的条件有直线与平面内的两条相交直
线垂直.
2. 需证明的结论是 =0.·【自主解答】(1)选B.当a与b不共线时,由c·a=0,c·b=0,可推出l⊥α;当a与b为共线向量时,由c·a=0,c·b=0,不能够推出l⊥α;l⊥α一定有c·a=0且c·b=0.
(2)因为OB=OC,AB=AC,OA=OA,
所以△OAC≌△OAB.所以∠AOC=∠AOB.
因为
所以 所以OA⊥BC.····【方法技巧】利用空间向量解决垂直问题的方法
(1)证明线线垂直的方法
证明线线垂直关键是确定直线的方向向量,看方向向量的数量积是否为0判断两直线是否垂直.
(2)证明与空间向量a,b,c有关的向量m,n垂直的方法.
先用向量a,b,c表示向量m,n,再求解向量m,n的数量积判断是否为0.【变式训练】已知|a|= |b|=4,m=a+b,n=a+λb,
〈a,b〉=135°,m⊥n,则λ=________.
【解题指南】利用m⊥n可得m·n=0进而建立与向量a,b有关
的等量关系,利用等量关系求字母的值.【解析】由m⊥n,得(a+b)·(a+λb)=0,
所以a2+(1+λ)a·b+λb2=0,
所以18+(λ+1)× ×4cos 135°+16λ=0,
即4λ+6=0,所以λ=
答案: 【补偿训练】如图,已知△ABC在平面α内,∠A=90°,DA⊥平面α,则直线CA与DB的位置关系是______.【解题指南】先找出与CA,DB对应的空间向量,再利用向量
间的关系判断两直线的位置关系.
【解析】因为
所以CA⊥DB.
答案:垂直····【拓展类型】数量积的应用
【备选例题】(1)设A,B,C,D是空间
不共面的四点,且满足
则△BCD是( )
A.钝角三角形 B.锐角三角形
C.直角三角形 D.不确定···(2)如图所示,如果直线AB与平面α交于点B,且与平面α内的经过点B的三条直线BC,BD,BE所成的角相等.求证:AB⊥平面α.【解析】(1)选B.如图所示,
设
所以 =(a-b)·(c-b)
=a·c-b·c-a·b+b2=b2>0.
同理
所以△BCD的各内角均为锐角,即△BCD为锐角三角形.···(2)在直线BC,BD,BE上取
因为 与 所成的角相等,
所以
所以·····即
所以AB⊥DC,AB⊥DE.
又DC∩DE=D,
所以AB⊥平面α.··【方法技巧】
1.判断三角形的形状
利用数量积的符号可以判断两向量夹角是钝角、锐角还是直角,进而能够判断对应三角形的形状.
2.证明垂直
利用两向量数量积是否等于0,判断两向量是否垂直,进而可判断与垂直有关的几何问题.【规范解答】利用向量的数量积求异面直线所成的角
【典例】(12分)如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,
AB=BC=1,AA1= ,求异面直线BA1与AC所成角的余弦值.【审题】抓信息,找思路【解题】明步骤,得高分【点题】警误区,促提升
失分点1:解题时若忽视条件∠ABC=90°,即得不出①处的
结论,则本例基本不得分.
失分点2:解题时若忽视直三棱柱的条件,则不能得出②处结
论 则实际的考试中最多得2分.
失分点3:解题时若忽视异面直线所成角的范围,导致③处结
果写为 则实际的考试中至少会扣掉2分.··【悟题】提措施,导方向
1.关注两种意识
(1)范围意识:对于异面直线所成角,要注意其所成角的范围
为 余弦值的范围为[0,1).
(2)转化意识:把异面直线所成角与直线方向向量所成角进行
合理转化.2.关注向量表示
在运用向量进行计算时注意,找部分夹角特殊,长度特殊的向
量用这样的向量表示直线的方向向量,如本例中用
表示所求解的向量.
3.利用向量法求两异面直线的夹角的关注点
利用向量的数量积求出两向量的夹角,则这个夹角就是两异面
直线所成的角或者是其补角(注意异面直线所成角的范围).如
本例中两异面直线所成角的余弦值为正数,而非负数.【类题试解】已知在正方体中,M,N分别为棱BC和棱CC1的中点,求异面直线AC和MN所成的角.【解析】设正方体的棱长为2.
所以
又 即
所以
所以〈 〉=60°,
即异面直线AC和MN所成的角为60°.········
