3.1.4 空间向量的正交分解及其坐标表示 课件2
文档属性
| 名称 | 3.1.4 空间向量的正交分解及其坐标表示 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 980.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 18:30:33 | ||
图片预览











文档简介
课件59张PPT。3.1.4
空间向量的正交分解及其坐标表示1.空间向量的分解
(1)条件:i,j,k是空间三个_________的向量.
(2)结论:对空间任一向量p,存在一个有序实数组{x,y,z},使
得p=xi+yj+zk,我们称_________为向量p在i,j,k上的分向量.
2.空间向量基本定理
(1)条件:向量a,b,c_______.
(2)结论:对空间任一向量p,存在有序实数组{x,y,z},使得
p=_________.两两垂直xi,yj,zk不共面xa+yb+zc3.基底
(1){a,b,c}是空间的一个基底的条件:a,b,c_______.
(2)基向量:空间的一个基底{a,b,c}中的向量a,b,c叫做基向量.
(3)单位正交基底:向量e1,e2,e3为有__________且___________
_________.不共面公共起点O两两垂直的单位向量4.空间直角坐标系
(1)原点:以单位正交基底e1,e2,e3的__________为原点.
(2)方向:分别以e1,e2,e3的方向为x轴、y轴、z轴_______.
(3)坐标:若向量p=xe1+ye2+ze3,则把x,y,z称作向量p在单位
正交基底e1,e2,e3下的坐标.记作p=________.公共起点O正方向(x,y,z)1.判一判(正确的打“√”,错误的打“×”)
(1)只有两两垂直的三个向量才能作为空间向量的一组基底.( )
(2)向量 的坐标与点P的坐标一致.( )
(3)对于三个不共面向量a1,a2,a3,不存在实数组{λ1,λ2,λ3}
使0=λ1a1+λ2a2+λ3a3.( )【解析】(1)错误.只要三个向量不共面就可作为空间向量的一组基底,故此种说法错误.
(2)错误.向量的坐标不一定对应点的坐标,只有以原点为起点的向量的坐标与对应有向线段终点的坐标一致.
(3)错误.由空间向量基本定理,对空间中的任意向量a都存在有序实数组{λ1,λ2,λ3},使得a=λ1a1+λ2a2+λ3a3,故此种说法错误.
答案:(1)× (2)× (3)×2.做一做(请把正确的答案写在横线上)
(1)若向量i,j,k为空间直角坐标系上对应x轴,y轴,z轴正方向的单位向量,且设a=2i-j+3k,则向量a的坐标为 .
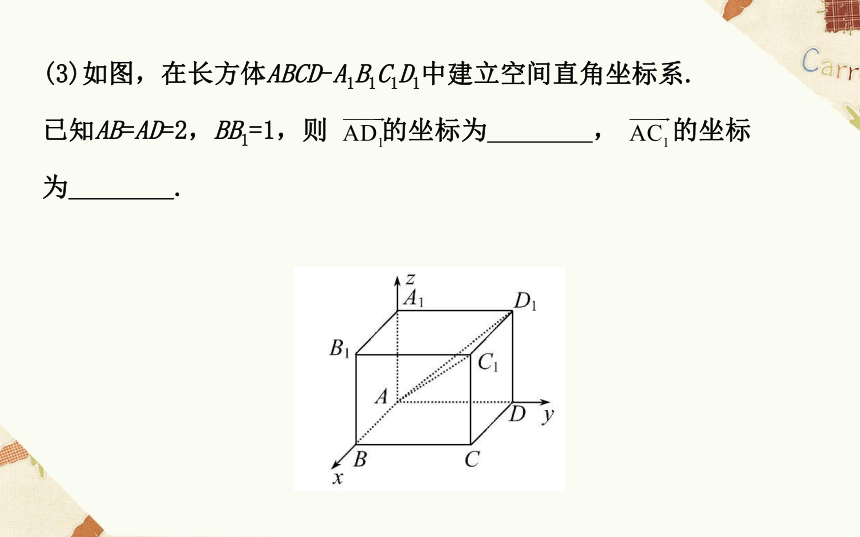
(2)若向量a,b,c为空间向量的正交基底,则向量a,b,c的位置关系是 .(3)如图,在长方体ABCD-A1B1C1D1中建立空间直角坐标系.
已知AB=AD=2,BB1=1,则 的坐标为 , 的坐标
为 .【解析】(1)由向量的单位正交表示知向量a的坐标为(2,-1,3).
答案:(2,-1,3)
(2)由正交基底的定义知,只有当向量a,b,c两两垂直时,才能成
为空间向量的正交基底,故向量a,b,c的位置关系是两两垂直.
答案:两两垂直
(3)根据已建立的空间直角坐标系知A(0,0,0),C1(2,2,1),
D1(0,2,1),则 的坐标为(0,2,1), 的坐标为(2,2,1).
答案:(0,2,1) (2,2,1)【要点探究】
知识点1 空间向量基本定理
空间向量基本定理的三个关注点:
(1)空间任意向量:用空间三个不共面的向量a,b,c可以线性表示出空间中任意一个向量,而且表示的结果是惟一的.
(2)基底的选取:空间任意三个不共面的向量都可以作为空间向量的一个基底.(3)顺序性:向量的坐标顺序必须与基底中的基向量对应,即若基底为{e1,e2,e3},p=xe1+ye2+ze3,则p的坐标为(x,y,z).【知识拓展】
1.空间向量基本定理的证明
存在性证明的四个步骤(如图)
(1)平移:把不共面的向量a,b,c与
向量p平移到公共的起点O上,使 =a,
=b, =c, =p.(2)平行投影:过点P作直线PP′平行于OC,交平面OAB于点
P′;在平面OAB内,过点P′作直线P′A′∥OB,P′B′∥OA,分别与直线OA,OB相交于点A′,B′.
(3)表示:存在三个实数x,y,z,使
(4)求和代入:2.空间向量基本定理中实数组{x,y,z}惟一性的证明
设还有实数x′,y′,z′,使p=x′a+y′b+z′c,
因为p=xa+yb+zc,则x′a+y′b+z′c=xa+yb+zc,所以有(x′-x)a+(y′-y)b+(z′-z)c=0.
又因为a,b,c不共面,所以有x=x′,y=y′,z=z′,故空间向量基本定理中实数组{x,y,z}是惟一的.【微思考】
(1)空间向量的基底与基向量是同一概念吗?
提示:不是.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
(2)0可以是基向量吗?
提示:不可以.由于0可看作是与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含它们都不是0.【即时练】
在以下三个命题中,真命题的个数是( )
①三个非零向量a,b,c不能构成空间的一个基底,则a,b,c共面;
②若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线;
③若a,b是两个不共线的向量,而c=λa+μb(λ,μ∈R且λμ≠0),则{a,b,c}构成空间的一个基底.
A.0 B.1 C.2 D.3【解析】选C.①正确,基底的向量必须不共面;②正确;③不对,a,b不共线,当c=λa+μb时,a,b,c共面,故只有①②正确.知识点2 空间向量的正交分解及坐标表示
1.单位正交基底的特点:
(1)位置:三个向量两两垂直且有公共起点O.
(2)模长:每个向量的模都等于1.
(3)记法:一般记作{e1,e2,e3},{i,j,k}等.2.空间直角坐标系:
以单位正交基底e1,e2,e3的公共起点O为原点,以e1,e2,e3的方向为x轴、y轴、z轴正方向的空间坐标系要注意的五点:
①记法:空间坐标系O-xyz;
②坐标面:经过任意两个轴的平面为坐标面,它们分别为xOy面,xOz面和yOz面;③坐标向量:e1,e2,e3叫坐标向量;
④画法:一般使用∠xOy=45°或135°,∠yOz=90°;
⑤点的坐标:p=xe1+ye2+ze3则p=(x,y,z),x,y,z分别叫横坐标、纵坐标、竖坐标.【微思考】
(1)在空间几何图形中建立空间直角坐标系的关键是什么?
提示:关键是利用几何图形特征,尽量寻找三条两两垂直且交于一点的直线,若找不到则应想法构建.
(2)同一个几何体中的点在不同的空间直角坐标系下坐标是否相同?
提示:由于建立的坐标系不同,从而各点在不同的坐标系下坐标不一定相同,但本质是一样的.【即时练】
已知A(2,3-μ,-1+ν)关于x轴的对称点是A′(λ,7,-6),则λ,μ,ν的值为( )
A.λ=-2,μ=-4,ν=-5 B.λ=2,μ=-4,ν=-5
C.λ=-2,μ=10,ν=8 D.λ=2,μ=10,ν=7
【解析】选D.因为点A(2,3-μ,-1+ν)关于x轴的对称点是横坐标不变,纵坐标与竖坐标变为原来的相反数,即为(2,μ-3,1-ν),所以有λ=2,μ-3=7,1-ν=-6,即λ=2,μ=10,ν=7.【题型示范】
类型一 基底的概念
【典例1】
(1)设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下列向量组:
①{a,b,x};②{x,y,z};
③{b,c,z};④{x,y,a+b+c}.
其中可以作为空间的基底的向量组有 个.(2)已知{e1,e2,e3}是空间的一个基底,且 =e1+2e2-e3,
=-3e1+e2+2e3, =e1+e2-e3,试判断{ }能否作为空
间的一个基底.【解题探究】1.题(1)中由x=a+b,y=b+c,z=c+a可想到向量的哪
一种运算法则?可构造哪一种空间图形来表示对应向量,从而说
明向量是否共面?
2.题(2)中若要判断向量 共面需满足的关系式是什么?
【探究提示】1.由x=a+b,y=b+c,z=c+a可联想到向量运算的平
行四边形法则,可利用长方体中的有向线段表示对应向量.
2.若向量 共面,则有 成立.【自主解答】(1)如图所示,设a=
a+b+c= 由A,B1,D1,C四点不共面
可知向量x,y,z也不共面.同理可知b,
c,z和x,y,a+b+c也不共面,可以作为
空间的基底.因x=a+b,故a,b,x共面,故不能作为基底.
故可为空间基底的向量组共有3个.
答案:3(2)假设 共面,由向量共面的充要条件知存在实数
x,y,使 成立.
所以 =e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)
=(-3x+y)e1+(x+y)e2+(2x-y)e3.
得 无解,
故 不共面,可以构成空间的一个基底.【方法技巧】基底的判断
判断某一向量组能否作为基底,关键是判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.【变式训练】设命题p:空间向量a,b,c是三个非零向量;命题q:{a,b,c}为空间向量的一个基底,则命题p是命题q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件【解题指南】从基底的定义和充要条件判断思考,先由p判断q是否成立,再由q判断p是否成立.
【解析】选B.当三个向量a,b,c共面时,a,b,c不能构成空间向量的一个基底,但是当{a,b,c}为空间向量的一个基底时,必有a,b,c为非零向量.因此命题p是命题q的必要不充分条件.
【误区警示】易错选A,忽视构成基底的三个向量满足的条件而导致错误.【补偿训练】若{a,b,c}是空间的一个基底,且存在实数x,y,z
使得xa+yb+zc=0,则x,y,z满足的条件是 .
【解析】若x≠0,则a= 即a与b,c共面.由{a,b,c}
是空间向量的一个基底,知a,b,c不共面,故x=0,同理y=z=0.
答案:x=y=z=0 类型二 用基底表示向量
【典例2】
(1)在四面体O-ABC中, D为BC的中点,
E为AD的中点,则 =( )(2)如图,已知平行六面体ABCD-A1B1C1D1,
设 试用a,b,c表示【解题探究】1.题(1)中向量 在哪个三角形中,能得到的
向量关系式是什么?
2.题(2)中向量 在哪个三角形或平行四边形中, 与
的关系是什么样的?
【探究提示】1. 在三角形OAE中,向量
2.连接AN,则 在三角形AMN中,在平行四边形ABCD中【自主解答】(1)选C.
(2)连接AN,则
由ABCD是平行四边形,得
则又
故
故【延伸探究】若题(2)结论改为用向量a,b,c表示 ,则结果如何?
【解析】连接 ,则
故【方法技巧】用基底表示向量的技巧
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间向量的一个基底{a,b,c}可以表示出空间所有向量.表示要彻底、结果中只能含有a,b,c,不能含有其他形式的向量.【变式训练】四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.
设 E,F分别是PC和PB的中点,试用a,b,
c表示
【解题指南】结合已知和所求,画出图形,联想相关的运算法
则和公式,再对照目标及基底,将所求向量反复分拆,直到全
部可以用基底表示为止.【解析】连接BO,则
【补偿训练】在平行六面体ABCD-A1B1C1D1中,
设 E,F分别是AD1,BD的中点.
(1)用向量a,b,c表示
(2)若 =xa+yb+zc,求实数x,y,z的值.【解析】(1)如图,
所以x= ,y=- ,z=-1.类型三 空间向量的坐标表示
【典例3】
(1)已知在如图所示的长方体ABCD-A1B1C1D1中,E,F分别为
D1C1,B1C1的中点,若以{ }为基底,则向量 的
坐标为______,向量 的坐标为______,向量 的坐标为
_______.(2)已知PA垂直于正方形ABCD所在的平面,M,N分别是CD,PC
的中点,并且PA=AD=1.在如图所示的空间直角坐标系中,
求向量 的坐标.【解题探究】1.题(1)中若求向量 及 的坐标,首先
应如何处理?
2.图形中的哪些向量可作为单位正交基底?如何用这个基底表
示向量 ?
【探究提示】1.应先用 表示出所求向量 及
2.因为AP=AD=AB=1,故可把向量 看作单位正交基
底,可利用三角形法则或平行四边形法则把向量 写成
的形式,即可得向量的坐标.【自主解答】(1)
所以 相对于基底{ }的坐标为
所以 的坐标为
所以 的坐标为(1,1,1).
答案:(2)因为PA=AD=AB=1,
所以可设
因为
所以【方法技巧】用坐标表示空间向量的步骤【变式训练】已知ABCD-A1B1C1D1是棱长为2的正方体,E,F分
别为BB1和DC的中点,建立如图所示的空间直角坐标系,试写
出 的坐标.【解析】设x,y,z轴的单位向量分别为e1,e2,e3,其方向
与各轴上的正方向相同,
则 =2e1+2e2+2e3,所以 =(2,2,2).
因为 =2e1+2e2+e3,所以 =(2,2,1).
又因为 =e2,所以 =(0,1,0).【补偿训练】已知正四面体ABCD棱长为a,试建立恰当的坐标
系并表示出各个顶点的坐标.
【解析】过A作AG垂直于平面BCD,
由于AB=AC=AD,所以G为△BCD的重心,
过G作GF∥CD,E为CD的中点,连结BE,
则BE⊥CD,以G为原点, 分别
为x轴,y轴,z轴,建立如图所示的空间直角坐标系.因为△BCD的边长为a,
则
又 ,所以
又BG= 所以AG=
所以【易错误区】求解空间点的坐标时建系不当致误
【典例】如图,在正三棱柱ABC-A1B1C1中,
已知△ABC的边长为1,三棱柱的高为2,建
立适当的空间直角坐标系,则 的
坐标分别为_________, _________.【解析】分别取BC,B1C1的中点D,D1,以D为原点,分别
以 的方向为x轴,y轴,z轴的
正方向建立空间直角坐标系,
如图所示,则
所以
答案: (答案不惟一)【常见误区】【防范措施】
建立恰当坐标系求解点的坐标
在解题时,建立适当的空间直角坐标系是解答关键,如本例中若选取点B(或A)为原点,应注意BA与BC(或AB与AC)不垂直,此时需要在平面ABC中作FB⊥BC(或EA⊥AC),否则易出现错误.【类题试解】在直三棱柱ABO-A1B1O1中,∠AOB= AO=4,
BO=2,AA1=4,D为A1B1的中点,在如图所示的空间直角坐
标系中, 的坐标分别为_______,________.【解析】(1)因为
又 所以
(2)因为
又 所以 =(-4,2,-4).
答案:(-2,-1,-4) (-4,2,-4)
空间向量的正交分解及其坐标表示1.空间向量的分解
(1)条件:i,j,k是空间三个_________的向量.
(2)结论:对空间任一向量p,存在一个有序实数组{x,y,z},使
得p=xi+yj+zk,我们称_________为向量p在i,j,k上的分向量.
2.空间向量基本定理
(1)条件:向量a,b,c_______.
(2)结论:对空间任一向量p,存在有序实数组{x,y,z},使得
p=_________.两两垂直xi,yj,zk不共面xa+yb+zc3.基底
(1){a,b,c}是空间的一个基底的条件:a,b,c_______.
(2)基向量:空间的一个基底{a,b,c}中的向量a,b,c叫做基向量.
(3)单位正交基底:向量e1,e2,e3为有__________且___________
_________.不共面公共起点O两两垂直的单位向量4.空间直角坐标系
(1)原点:以单位正交基底e1,e2,e3的__________为原点.
(2)方向:分别以e1,e2,e3的方向为x轴、y轴、z轴_______.
(3)坐标:若向量p=xe1+ye2+ze3,则把x,y,z称作向量p在单位
正交基底e1,e2,e3下的坐标.记作p=________.公共起点O正方向(x,y,z)1.判一判(正确的打“√”,错误的打“×”)
(1)只有两两垂直的三个向量才能作为空间向量的一组基底.( )
(2)向量 的坐标与点P的坐标一致.( )
(3)对于三个不共面向量a1,a2,a3,不存在实数组{λ1,λ2,λ3}
使0=λ1a1+λ2a2+λ3a3.( )【解析】(1)错误.只要三个向量不共面就可作为空间向量的一组基底,故此种说法错误.
(2)错误.向量的坐标不一定对应点的坐标,只有以原点为起点的向量的坐标与对应有向线段终点的坐标一致.
(3)错误.由空间向量基本定理,对空间中的任意向量a都存在有序实数组{λ1,λ2,λ3},使得a=λ1a1+λ2a2+λ3a3,故此种说法错误.
答案:(1)× (2)× (3)×2.做一做(请把正确的答案写在横线上)
(1)若向量i,j,k为空间直角坐标系上对应x轴,y轴,z轴正方向的单位向量,且设a=2i-j+3k,则向量a的坐标为 .
(2)若向量a,b,c为空间向量的正交基底,则向量a,b,c的位置关系是 .(3)如图,在长方体ABCD-A1B1C1D1中建立空间直角坐标系.
已知AB=AD=2,BB1=1,则 的坐标为 , 的坐标
为 .【解析】(1)由向量的单位正交表示知向量a的坐标为(2,-1,3).
答案:(2,-1,3)
(2)由正交基底的定义知,只有当向量a,b,c两两垂直时,才能成
为空间向量的正交基底,故向量a,b,c的位置关系是两两垂直.
答案:两两垂直
(3)根据已建立的空间直角坐标系知A(0,0,0),C1(2,2,1),
D1(0,2,1),则 的坐标为(0,2,1), 的坐标为(2,2,1).
答案:(0,2,1) (2,2,1)【要点探究】
知识点1 空间向量基本定理
空间向量基本定理的三个关注点:
(1)空间任意向量:用空间三个不共面的向量a,b,c可以线性表示出空间中任意一个向量,而且表示的结果是惟一的.
(2)基底的选取:空间任意三个不共面的向量都可以作为空间向量的一个基底.(3)顺序性:向量的坐标顺序必须与基底中的基向量对应,即若基底为{e1,e2,e3},p=xe1+ye2+ze3,则p的坐标为(x,y,z).【知识拓展】
1.空间向量基本定理的证明
存在性证明的四个步骤(如图)
(1)平移:把不共面的向量a,b,c与
向量p平移到公共的起点O上,使 =a,
=b, =c, =p.(2)平行投影:过点P作直线PP′平行于OC,交平面OAB于点
P′;在平面OAB内,过点P′作直线P′A′∥OB,P′B′∥OA,分别与直线OA,OB相交于点A′,B′.
(3)表示:存在三个实数x,y,z,使
(4)求和代入:2.空间向量基本定理中实数组{x,y,z}惟一性的证明
设还有实数x′,y′,z′,使p=x′a+y′b+z′c,
因为p=xa+yb+zc,则x′a+y′b+z′c=xa+yb+zc,所以有(x′-x)a+(y′-y)b+(z′-z)c=0.
又因为a,b,c不共面,所以有x=x′,y=y′,z=z′,故空间向量基本定理中实数组{x,y,z}是惟一的.【微思考】
(1)空间向量的基底与基向量是同一概念吗?
提示:不是.一个基底是一个向量组,一个基向量是指基底中的某一个向量,二者是相关联的不同概念.
(2)0可以是基向量吗?
提示:不可以.由于0可看作是与任意一个非零向量共线,与任意两个非零向量共面,所以三个向量不共面,就隐含它们都不是0.【即时练】
在以下三个命题中,真命题的个数是( )
①三个非零向量a,b,c不能构成空间的一个基底,则a,b,c共面;
②若两个非零向量a,b与任何一个向量都不能构成空间的一个基底,则a,b共线;
③若a,b是两个不共线的向量,而c=λa+μb(λ,μ∈R且λμ≠0),则{a,b,c}构成空间的一个基底.
A.0 B.1 C.2 D.3【解析】选C.①正确,基底的向量必须不共面;②正确;③不对,a,b不共线,当c=λa+μb时,a,b,c共面,故只有①②正确.知识点2 空间向量的正交分解及坐标表示
1.单位正交基底的特点:
(1)位置:三个向量两两垂直且有公共起点O.
(2)模长:每个向量的模都等于1.
(3)记法:一般记作{e1,e2,e3},{i,j,k}等.2.空间直角坐标系:
以单位正交基底e1,e2,e3的公共起点O为原点,以e1,e2,e3的方向为x轴、y轴、z轴正方向的空间坐标系要注意的五点:
①记法:空间坐标系O-xyz;
②坐标面:经过任意两个轴的平面为坐标面,它们分别为xOy面,xOz面和yOz面;③坐标向量:e1,e2,e3叫坐标向量;
④画法:一般使用∠xOy=45°或135°,∠yOz=90°;
⑤点的坐标:p=xe1+ye2+ze3则p=(x,y,z),x,y,z分别叫横坐标、纵坐标、竖坐标.【微思考】
(1)在空间几何图形中建立空间直角坐标系的关键是什么?
提示:关键是利用几何图形特征,尽量寻找三条两两垂直且交于一点的直线,若找不到则应想法构建.
(2)同一个几何体中的点在不同的空间直角坐标系下坐标是否相同?
提示:由于建立的坐标系不同,从而各点在不同的坐标系下坐标不一定相同,但本质是一样的.【即时练】
已知A(2,3-μ,-1+ν)关于x轴的对称点是A′(λ,7,-6),则λ,μ,ν的值为( )
A.λ=-2,μ=-4,ν=-5 B.λ=2,μ=-4,ν=-5
C.λ=-2,μ=10,ν=8 D.λ=2,μ=10,ν=7
【解析】选D.因为点A(2,3-μ,-1+ν)关于x轴的对称点是横坐标不变,纵坐标与竖坐标变为原来的相反数,即为(2,μ-3,1-ν),所以有λ=2,μ-3=7,1-ν=-6,即λ=2,μ=10,ν=7.【题型示范】
类型一 基底的概念
【典例1】
(1)设x=a+b,y=b+c,z=c+a,且{a,b,c}是空间的一个基底.给出下列向量组:
①{a,b,x};②{x,y,z};
③{b,c,z};④{x,y,a+b+c}.
其中可以作为空间的基底的向量组有 个.(2)已知{e1,e2,e3}是空间的一个基底,且 =e1+2e2-e3,
=-3e1+e2+2e3, =e1+e2-e3,试判断{ }能否作为空
间的一个基底.【解题探究】1.题(1)中由x=a+b,y=b+c,z=c+a可想到向量的哪
一种运算法则?可构造哪一种空间图形来表示对应向量,从而说
明向量是否共面?
2.题(2)中若要判断向量 共面需满足的关系式是什么?
【探究提示】1.由x=a+b,y=b+c,z=c+a可联想到向量运算的平
行四边形法则,可利用长方体中的有向线段表示对应向量.
2.若向量 共面,则有 成立.【自主解答】(1)如图所示,设a=
a+b+c= 由A,B1,D1,C四点不共面
可知向量x,y,z也不共面.同理可知b,
c,z和x,y,a+b+c也不共面,可以作为
空间的基底.因x=a+b,故a,b,x共面,故不能作为基底.
故可为空间基底的向量组共有3个.
答案:3(2)假设 共面,由向量共面的充要条件知存在实数
x,y,使 成立.
所以 =e1+2e2-e3=x(-3e1+e2+2e3)+y(e1+e2-e3)
=(-3x+y)e1+(x+y)e2+(2x-y)e3.
得 无解,
故 不共面,可以构成空间的一个基底.【方法技巧】基底的判断
判断某一向量组能否作为基底,关键是判断它们是否共面.如果从正面难以入手,可用反证法或利用一些常见的几何图形进行判断.【变式训练】设命题p:空间向量a,b,c是三个非零向量;命题q:{a,b,c}为空间向量的一个基底,则命题p是命题q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件【解题指南】从基底的定义和充要条件判断思考,先由p判断q是否成立,再由q判断p是否成立.
【解析】选B.当三个向量a,b,c共面时,a,b,c不能构成空间向量的一个基底,但是当{a,b,c}为空间向量的一个基底时,必有a,b,c为非零向量.因此命题p是命题q的必要不充分条件.
【误区警示】易错选A,忽视构成基底的三个向量满足的条件而导致错误.【补偿训练】若{a,b,c}是空间的一个基底,且存在实数x,y,z
使得xa+yb+zc=0,则x,y,z满足的条件是 .
【解析】若x≠0,则a= 即a与b,c共面.由{a,b,c}
是空间向量的一个基底,知a,b,c不共面,故x=0,同理y=z=0.
答案:x=y=z=0 类型二 用基底表示向量
【典例2】
(1)在四面体O-ABC中, D为BC的中点,
E为AD的中点,则 =( )(2)如图,已知平行六面体ABCD-A1B1C1D1,
设 试用a,b,c表示【解题探究】1.题(1)中向量 在哪个三角形中,能得到的
向量关系式是什么?
2.题(2)中向量 在哪个三角形或平行四边形中, 与
的关系是什么样的?
【探究提示】1. 在三角形OAE中,向量
2.连接AN,则 在三角形AMN中,在平行四边形ABCD中【自主解答】(1)选C.
(2)连接AN,则
由ABCD是平行四边形,得
则又
故
故【延伸探究】若题(2)结论改为用向量a,b,c表示 ,则结果如何?
【解析】连接 ,则
故【方法技巧】用基底表示向量的技巧
(1)定基底:根据已知条件,确定三个不共面的向量构成空间的一个基底.
(2)找目标:用确定的基底(或已知基底)表示目标向量,需要根据三角形法则及平行四边形法则,结合相等向量的代换、向量的运算进行变形、化简,最后求出结果.
(3)下结论:利用空间向量的一个基底{a,b,c}可以表示出空间所有向量.表示要彻底、结果中只能含有a,b,c,不能含有其他形式的向量.【变式训练】四棱锥P-OABC的底面为一矩形,PO⊥平面OABC.
设 E,F分别是PC和PB的中点,试用a,b,
c表示
【解题指南】结合已知和所求,画出图形,联想相关的运算法
则和公式,再对照目标及基底,将所求向量反复分拆,直到全
部可以用基底表示为止.【解析】连接BO,则
【补偿训练】在平行六面体ABCD-A1B1C1D1中,
设 E,F分别是AD1,BD的中点.
(1)用向量a,b,c表示
(2)若 =xa+yb+zc,求实数x,y,z的值.【解析】(1)如图,
所以x= ,y=- ,z=-1.类型三 空间向量的坐标表示
【典例3】
(1)已知在如图所示的长方体ABCD-A1B1C1D1中,E,F分别为
D1C1,B1C1的中点,若以{ }为基底,则向量 的
坐标为______,向量 的坐标为______,向量 的坐标为
_______.(2)已知PA垂直于正方形ABCD所在的平面,M,N分别是CD,PC
的中点,并且PA=AD=1.在如图所示的空间直角坐标系中,
求向量 的坐标.【解题探究】1.题(1)中若求向量 及 的坐标,首先
应如何处理?
2.图形中的哪些向量可作为单位正交基底?如何用这个基底表
示向量 ?
【探究提示】1.应先用 表示出所求向量 及
2.因为AP=AD=AB=1,故可把向量 看作单位正交基
底,可利用三角形法则或平行四边形法则把向量 写成
的形式,即可得向量的坐标.【自主解答】(1)
所以 相对于基底{ }的坐标为
所以 的坐标为
所以 的坐标为(1,1,1).
答案:(2)因为PA=AD=AB=1,
所以可设
因为
所以【方法技巧】用坐标表示空间向量的步骤【变式训练】已知ABCD-A1B1C1D1是棱长为2的正方体,E,F分
别为BB1和DC的中点,建立如图所示的空间直角坐标系,试写
出 的坐标.【解析】设x,y,z轴的单位向量分别为e1,e2,e3,其方向
与各轴上的正方向相同,
则 =2e1+2e2+2e3,所以 =(2,2,2).
因为 =2e1+2e2+e3,所以 =(2,2,1).
又因为 =e2,所以 =(0,1,0).【补偿训练】已知正四面体ABCD棱长为a,试建立恰当的坐标
系并表示出各个顶点的坐标.
【解析】过A作AG垂直于平面BCD,
由于AB=AC=AD,所以G为△BCD的重心,
过G作GF∥CD,E为CD的中点,连结BE,
则BE⊥CD,以G为原点, 分别
为x轴,y轴,z轴,建立如图所示的空间直角坐标系.因为△BCD的边长为a,
则
又 ,所以
又BG= 所以AG=
所以【易错误区】求解空间点的坐标时建系不当致误
【典例】如图,在正三棱柱ABC-A1B1C1中,
已知△ABC的边长为1,三棱柱的高为2,建
立适当的空间直角坐标系,则 的
坐标分别为_________, _________.【解析】分别取BC,B1C1的中点D,D1,以D为原点,分别
以 的方向为x轴,y轴,z轴的
正方向建立空间直角坐标系,
如图所示,则
所以
答案: (答案不惟一)【常见误区】【防范措施】
建立恰当坐标系求解点的坐标
在解题时,建立适当的空间直角坐标系是解答关键,如本例中若选取点B(或A)为原点,应注意BA与BC(或AB与AC)不垂直,此时需要在平面ABC中作FB⊥BC(或EA⊥AC),否则易出现错误.【类题试解】在直三棱柱ABO-A1B1O1中,∠AOB= AO=4,
BO=2,AA1=4,D为A1B1的中点,在如图所示的空间直角坐
标系中, 的坐标分别为_______,________.【解析】(1)因为
又 所以
(2)因为
又 所以 =(-4,2,-4).
答案:(-2,-1,-4) (-4,2,-4)
