3.1.5 空间向量运算的坐标表示 课件2
文档属性
| 名称 | 3.1.5 空间向量运算的坐标表示 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 18:38:24 | ||
图片预览






文档简介
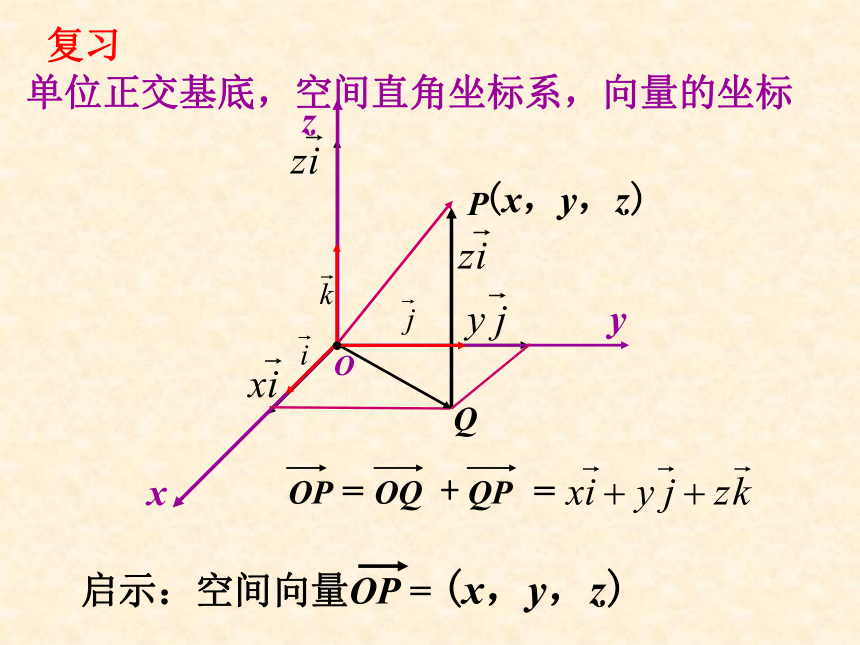
课件16张PPT。第三章 空间向量与立体几何3.1.5 空间向量运算的坐标表示单位正交基底,空间直角坐标系,向量的坐标O(x,y,z)复习则1.复习平面向量的坐标运算(1)设设M=(x,y),若M是线段AB的中点, 类比平面向量,空间向量的坐标运算是怎样的呢?则类比可得空间向量的坐标运算(1)设设M=(x,y,z),若M是线段AB的中点,2.平面向量的数量积、距离与夹角1.距离公式2.夹角公式类比可得空间向量的数量积、距离与夹角1.距离公式2.夹角公式数量积运算的证明:解:例题讲解:应用( )1.已知(1)(4)(2)(3)例2 如图,在正方体 中,
,求 与 所成的角的余弦值. 解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则 例2 如图,在正方体 中,
,求 与 所成的角的余弦值. 例3.如图,在正方体 中,E,F分别是
的中点,求证思考与交流: 1.若E1,F1分别是A'B'和C'D'
的一个四等分点,那么
又是多少呢?(1,1,0)F1E1(0,0,0)答案:2.已知a=(1,0),b=(m,m)(m>0),则〈a,b〉=________ 45° (1)熟练掌握空间向量坐标表示的各种运算律;确定空间几何体中顶点和向量的坐标. 课时小结(2)空间向量中的公式的形式与平面向量中相
关内容一致,因此可类比记忆. 1、重点:2、难点:
,求 与 所成的角的余弦值. 解:设正方体的棱长为1,如图建
立空间直角坐标系 ,则 例2 如图,在正方体 中,
,求 与 所成的角的余弦值. 例3.如图,在正方体 中,E,F分别是
的中点,求证思考与交流: 1.若E1,F1分别是A'B'和C'D'
的一个四等分点,那么
又是多少呢?(1,1,0)F1E1(0,0,0)答案:2.已知a=(1,0),b=(m,m)(m>0),则〈a,b〉=________ 45° (1)熟练掌握空间向量坐标表示的各种运算律;确定空间几何体中顶点和向量的坐标. 课时小结(2)空间向量中的公式的形式与平面向量中相
关内容一致,因此可类比记忆. 1、重点:2、难点:
