3.1.5 空间向量运算的坐标表示 课件3
文档属性
| 名称 | 3.1.5 空间向量运算的坐标表示 课件3 |  | |
| 格式 | zip | ||
| 文件大小 | 376.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 18:40:09 | ||
图片预览






文档简介
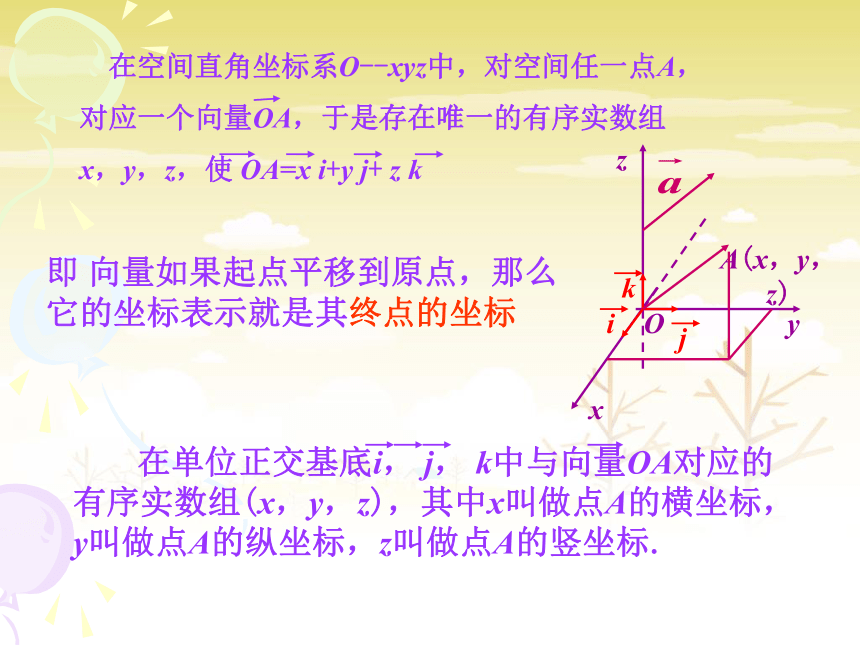
课件23张PPT。3.1.5空间向量运算的坐标表示复习引入:空间向量的基本定理:基底空间任意三个不共面向量都可以构成空间的一个基底思考:基底能不能含有零向量?一、空间直角坐标系zxxkw二、向量的直角坐标xyzOA(a1,a2,a3)ijk学.科.网即 向量如果起点平移到原点,那么
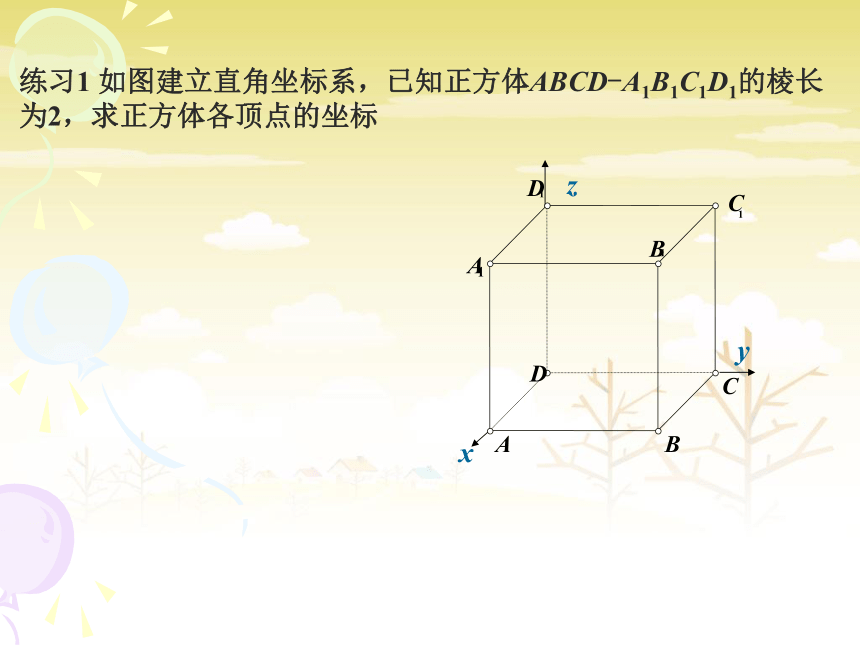
它的坐标表示就是其终点的坐标练习1 如图建立直角坐标系,已知正方体ABCD-A1B1C1D1的棱长
为2,求正方体各顶点的坐标
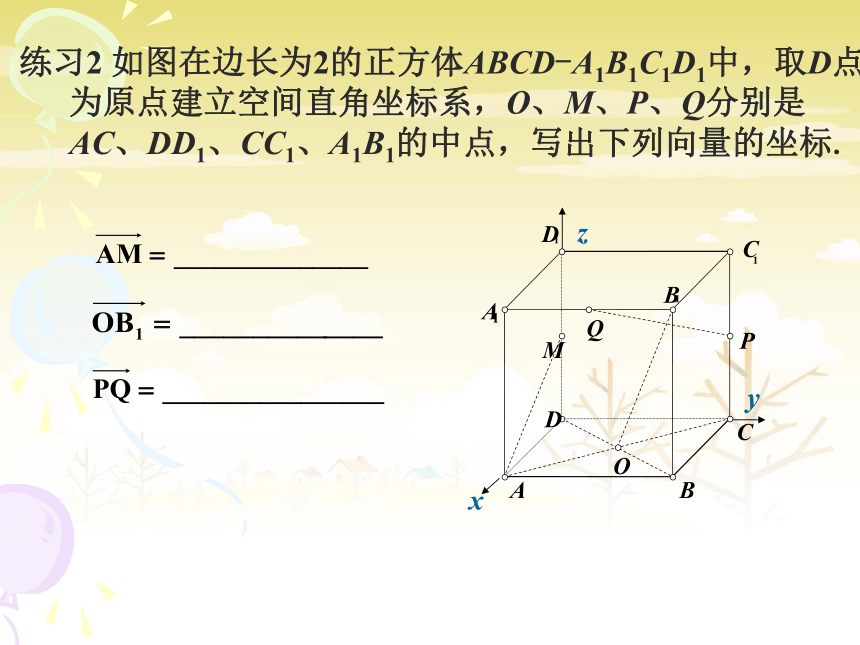
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标. 空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基底,进而确定各向量的坐标.练习2 如图在边长为2的正方体ABCD-A1B1C1D1中,取D点
为原点建立空间直角坐标系,O、M、P、Q分别是
AC、DD1、CC1、A1B1的中点,写出下列向量的坐标.
三、向量的直角坐标运算例1 已知 =(2,-3,5), =(-3,1,-4),求 + , - ,
8 ,
四、距离与夹角1.距离公式(1)向量的长度(模)公式注意:此公式的几何意义是表示长方体的对角线的长度.(2)空间两点间的距离公式(2)、两个向量夹角公式练习一:三、应用举例练习二:练习三:思考题:四、课堂小结:1.基本知识:(1)向量的长度公式与两点间的距离公式;(2)两个向量的夹角公式. 2.思想方法:用向量计算或证明几何问题
时,可以先建立直角坐标系,然后把向量、点坐
标化,借助向量的直角坐标运算法则进行计算或
证明.
它的坐标表示就是其终点的坐标练习1 如图建立直角坐标系,已知正方体ABCD-A1B1C1D1的棱长
为2,求正方体各顶点的坐标
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标. 空间向量坐标运算法则,关键是注意空间几何关系与向量坐标关系的转化,为此在利用向量的坐标运算判断空间几何关系时,首先要选定单位正交基底,进而确定各向量的坐标.练习2 如图在边长为2的正方体ABCD-A1B1C1D1中,取D点
为原点建立空间直角坐标系,O、M、P、Q分别是
AC、DD1、CC1、A1B1的中点,写出下列向量的坐标.
三、向量的直角坐标运算例1 已知 =(2,-3,5), =(-3,1,-4),求 + , - ,
8 ,
四、距离与夹角1.距离公式(1)向量的长度(模)公式注意:此公式的几何意义是表示长方体的对角线的长度.(2)空间两点间的距离公式(2)、两个向量夹角公式练习一:三、应用举例练习二:练习三:思考题:四、课堂小结:1.基本知识:(1)向量的长度公式与两点间的距离公式;(2)两个向量的夹角公式. 2.思想方法:用向量计算或证明几何问题
时,可以先建立直角坐标系,然后把向量、点坐
标化,借助向量的直角坐标运算法则进行计算或
证明.
