3.2.1 立体几何中的向量方法 课件1
文档属性
| 名称 | 3.2.1 立体几何中的向量方法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 743.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览



文档简介
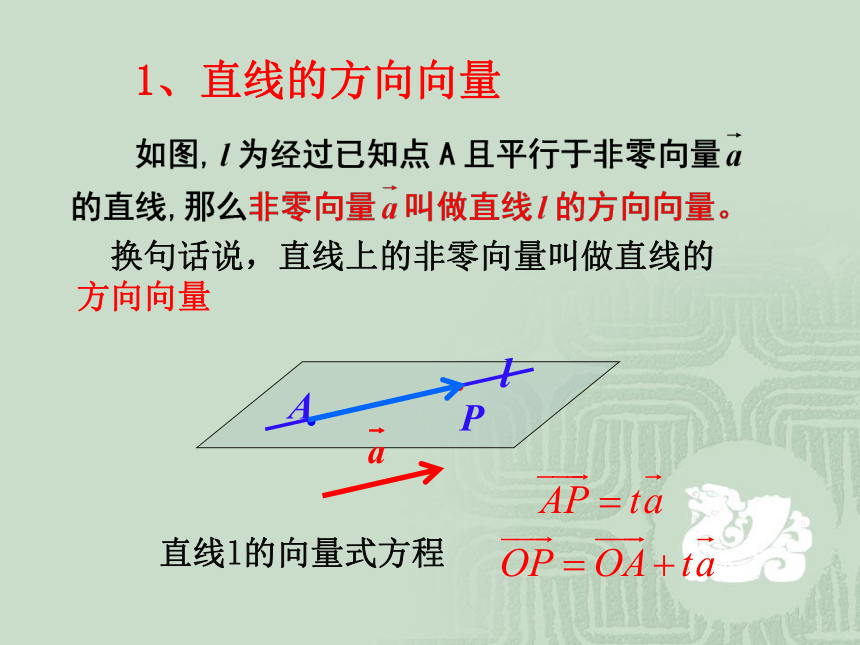
课件13张PPT。第三章 空间向量与立体几何3.2.1 立体几何中的向量方法1、直线的方向向量直线l的向量式方程 换句话说,直线上的非零向量叫做直线的
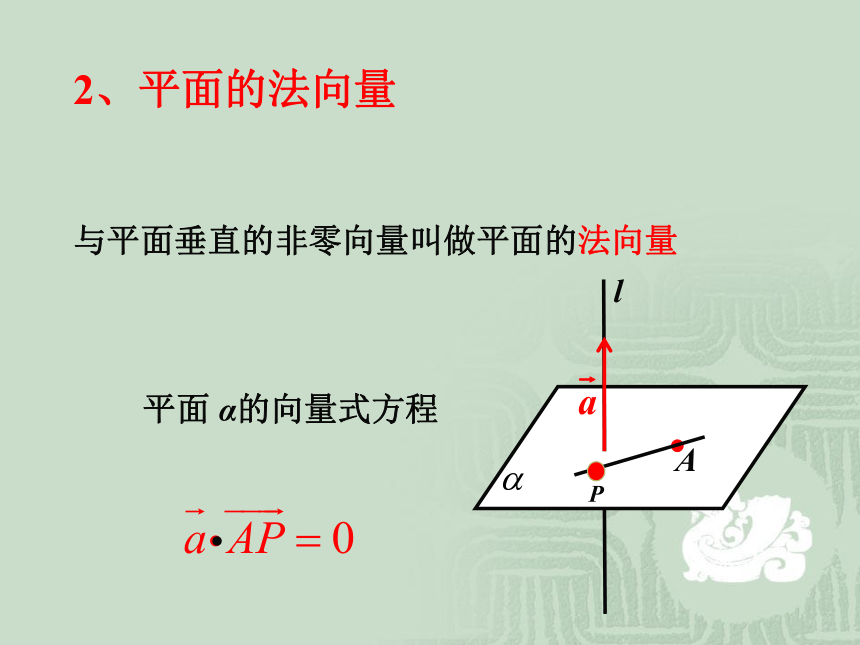
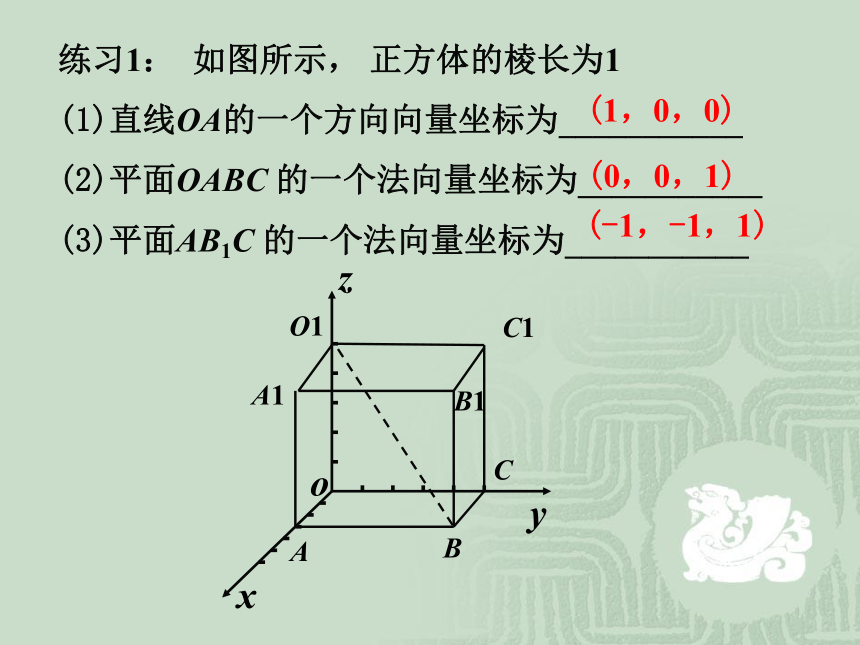
方向向量2、平面的法向量l平面 α的向量式方程与平面垂直的非零向量叫做平面的法向量.练习1: 如图所示, 正方体的棱长为1
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________(-1,-1,1)(0,0,1)(1,0,0)由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=1较合理.其实平面的法向量不是惟一的.
.. 练习4: 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC=1 ,E是PC
的中点, 求平面EDB的一个法向量.ABCDPE解:如图所示建立空间直角坐标系.设平面EDB的法向量为 定理 一个平面内的两条相交直线与另一个平面平行,
则这两个平面平行已知 直线l与m相交, αβlmml3、平行关系:3、平行关系:α3、平行关系:αβ②巩固性训练 设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交
方向向量2、平面的法向量l平面 α的向量式方程与平面垂直的非零向量叫做平面的法向量.练习1: 如图所示, 正方体的棱长为1
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________(-1,-1,1)(0,0,1)(1,0,0)由两个三元一次方程组成的方程组的解是不惟一的,为方便起见,取z=1较合理.其实平面的法向量不是惟一的.
.. 练习4: 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC=1 ,E是PC
的中点, 求平面EDB的一个法向量.ABCDPE解:如图所示建立空间直角坐标系.设平面EDB的法向量为 定理 一个平面内的两条相交直线与另一个平面平行,
则这两个平面平行已知 直线l与m相交, αβlmml3、平行关系:3、平行关系:α3、平行关系:αβ②巩固性训练 设 分别是平面α,β的法向量,根据
下列条件,判断α,β的位置关系.垂直平行相交
