3.2.2 立体几何中的向量方法 课件1
文档属性
| 名称 | 3.2.2 立体几何中的向量方法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 759.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览

文档简介
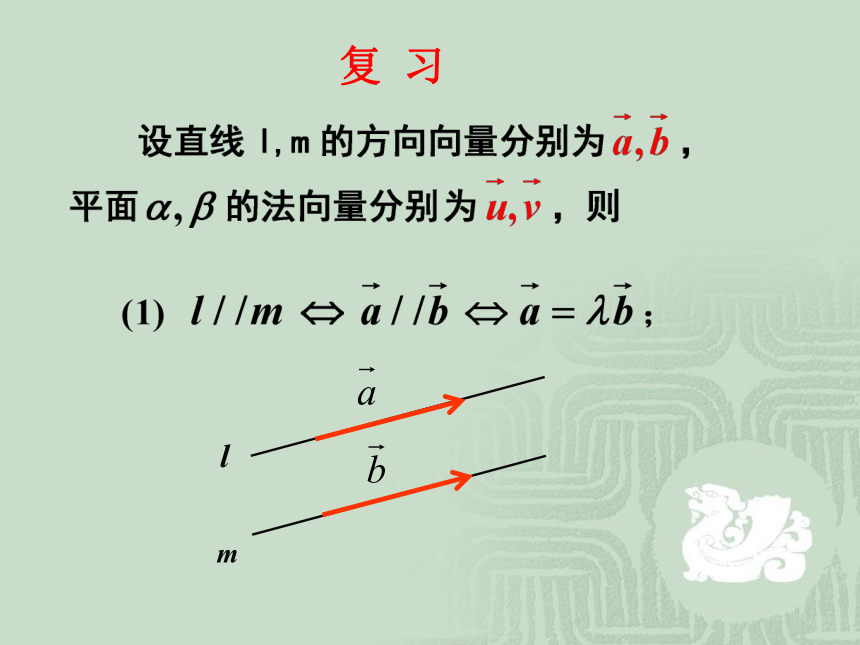
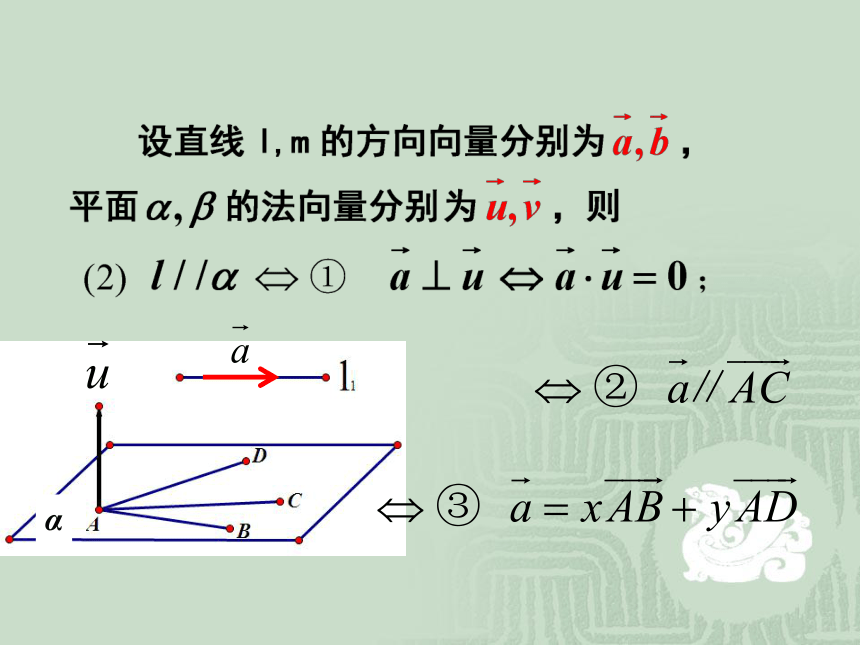
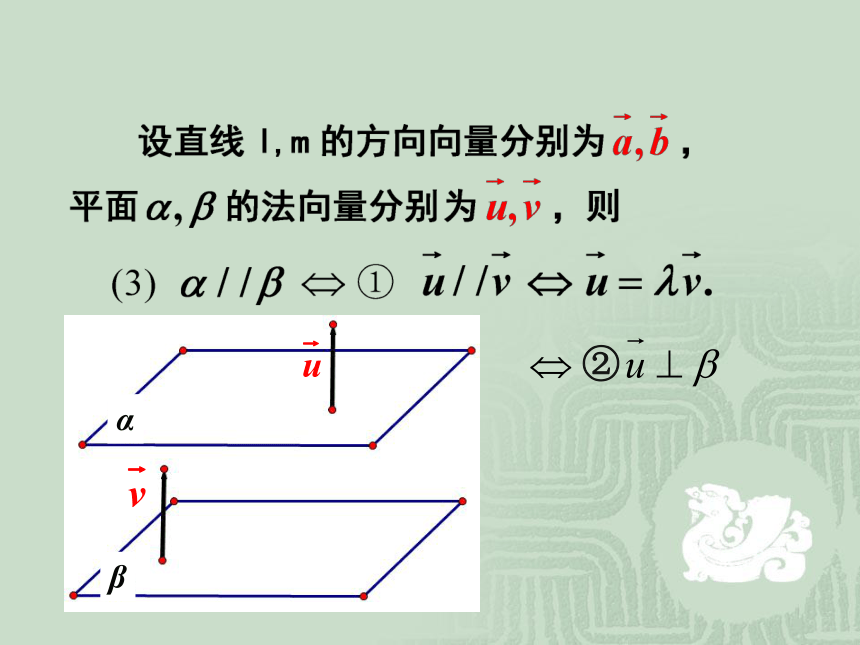
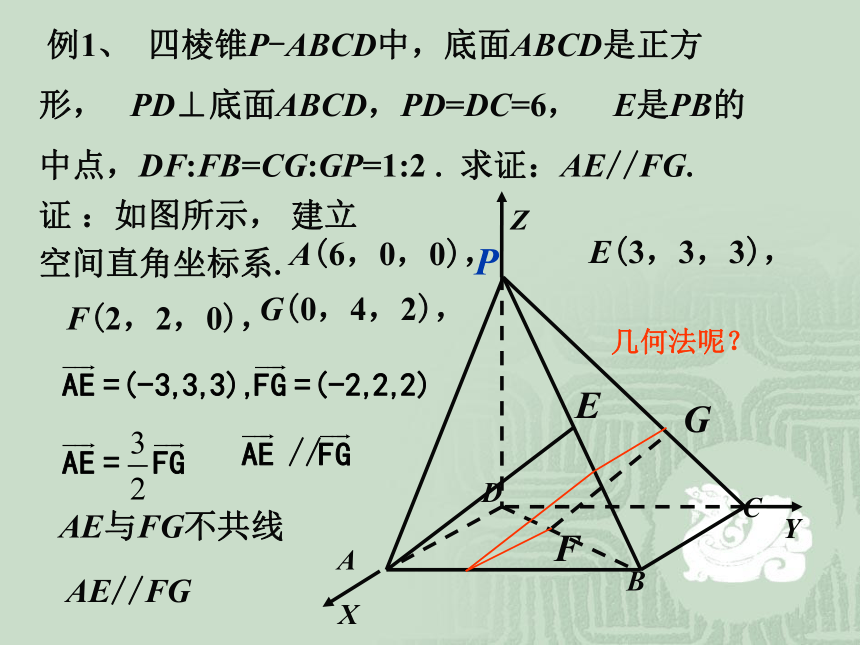
课件14张PPT。第三章 空间向量与立体几何3.2.2 立体几何中的向量方法ml复 习ααβ② 例1、 四棱锥P-ABCD中,底面ABCD是正方
形, PD⊥底面ABCD,PD=DC=6, E是PB的
中点,DF:FB=CG:GP=1:2 . 求证:AE//FG.ABCDPGFEA(6,0,0),F(2,2,0),E(3,3,3),G(0,4,2),AE//FG证 :如图所示, 建立
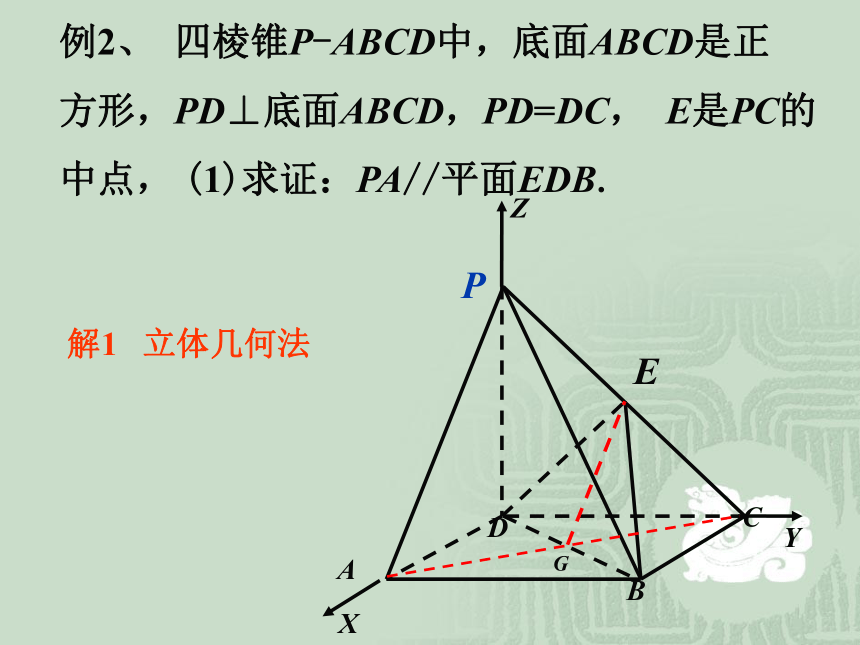
空间直角坐标系.AE与FG不共线几何法呢?例2、 四棱锥P-ABCD中,底面ABCD是正
方形,PD⊥底面ABCD,PD=DC, E是PC的
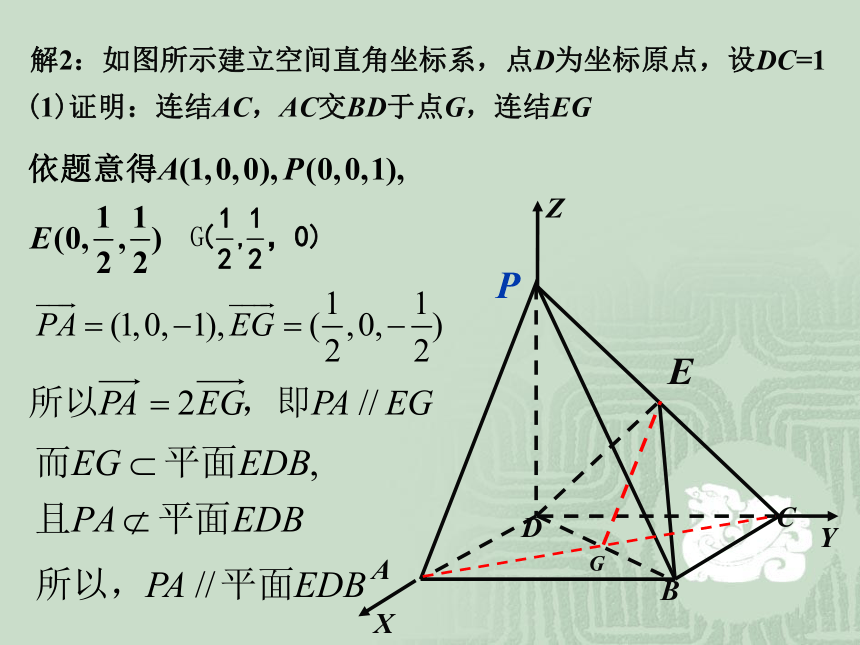
中点, (1)求证:PA//平面EDB.ABCDPE解1 立体几何法ABCDPE解2:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:连结AC,AC交BD于点G,连结EGABCDPE解3:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:设平面EDB的法向量为ABCDPE解4:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:解得 x=-2,y=1例3、如图,已知矩形和矩形所在平面相交于AD,点分别在对角线上,且求证:几何法呢?垂直关系:lm垂直关系:lABC垂直关系:αβ
形, PD⊥底面ABCD,PD=DC=6, E是PB的
中点,DF:FB=CG:GP=1:2 . 求证:AE//FG.ABCDPGFEA(6,0,0),F(2,2,0),E(3,3,3),G(0,4,2),AE//FG证 :如图所示, 建立
空间直角坐标系.AE与FG不共线几何法呢?例2、 四棱锥P-ABCD中,底面ABCD是正
方形,PD⊥底面ABCD,PD=DC, E是PC的
中点, (1)求证:PA//平面EDB.ABCDPE解1 立体几何法ABCDPE解2:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:连结AC,AC交BD于点G,连结EGABCDPE解3:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:设平面EDB的法向量为ABCDPE解4:如图所示建立空间直角坐标系,点D为坐标原点,设DC=1(1)证明:解得 x=-2,y=1例3、如图,已知矩形和矩形所在平面相交于AD,点分别在对角线上,且求证:几何法呢?垂直关系:lm垂直关系:lABC垂直关系:αβ
