3.2.3 立体几何中的向量方法 课件1
文档属性
| 名称 | 3.2.3 立体几何中的向量方法 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 808.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 00:00:00 | ||
图片预览

文档简介
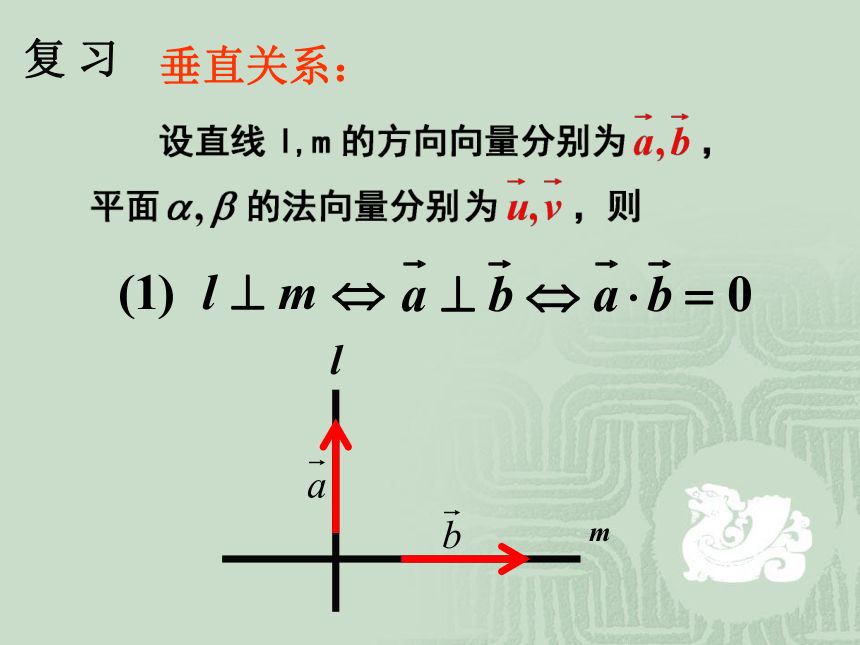
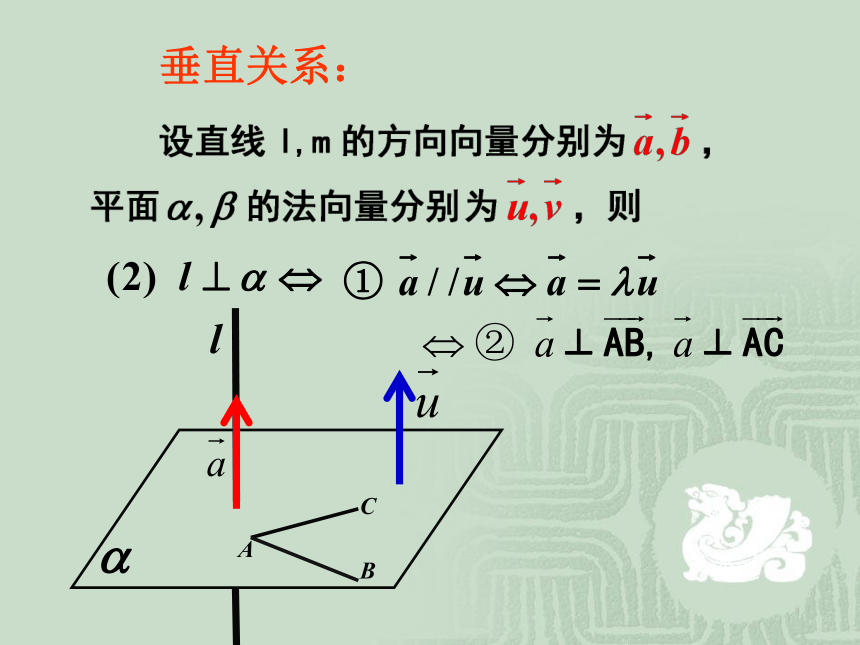
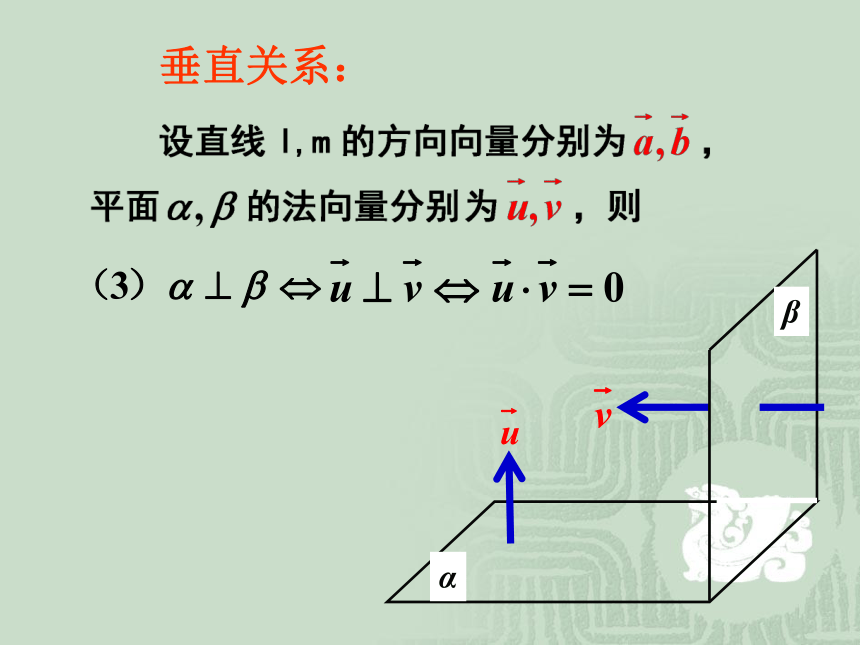
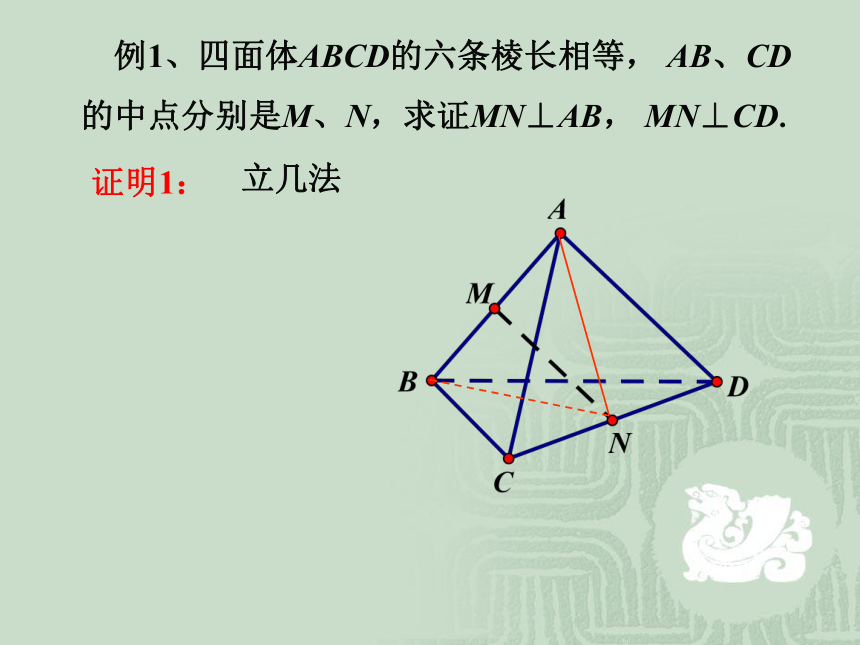
课件19张PPT。第三章 空间向量与立体几何3.2.3 立体几何中的向量方法垂直关系:lm复 习垂直关系:lABC垂直关系:αβ 例1、四面体ABCD的六条棱长相等, AB、CD
的中点分别是M、N,求证MN⊥AB, MN⊥CD. 立几法证明1: 例1、四面体ABCD的六条棱长相等, AB、CD
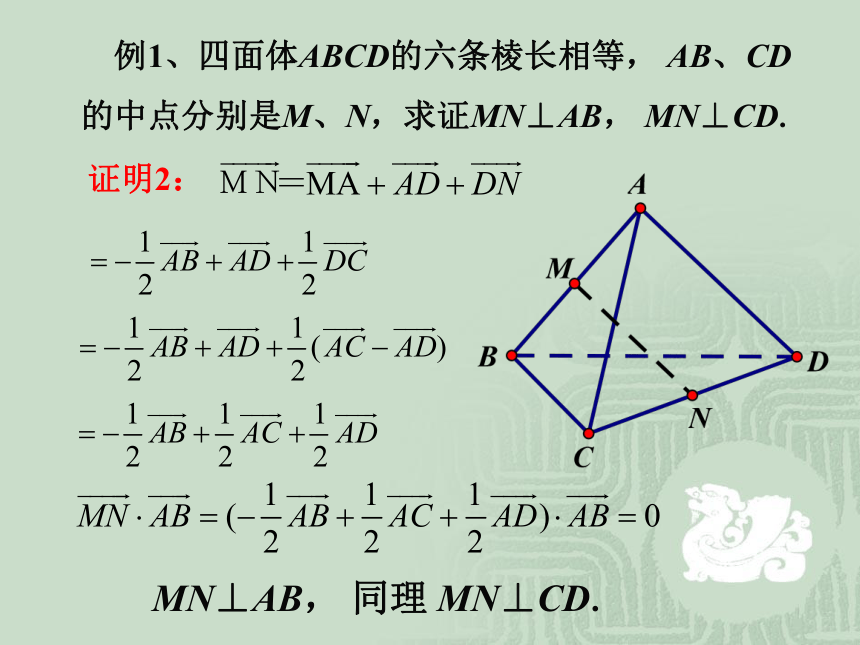
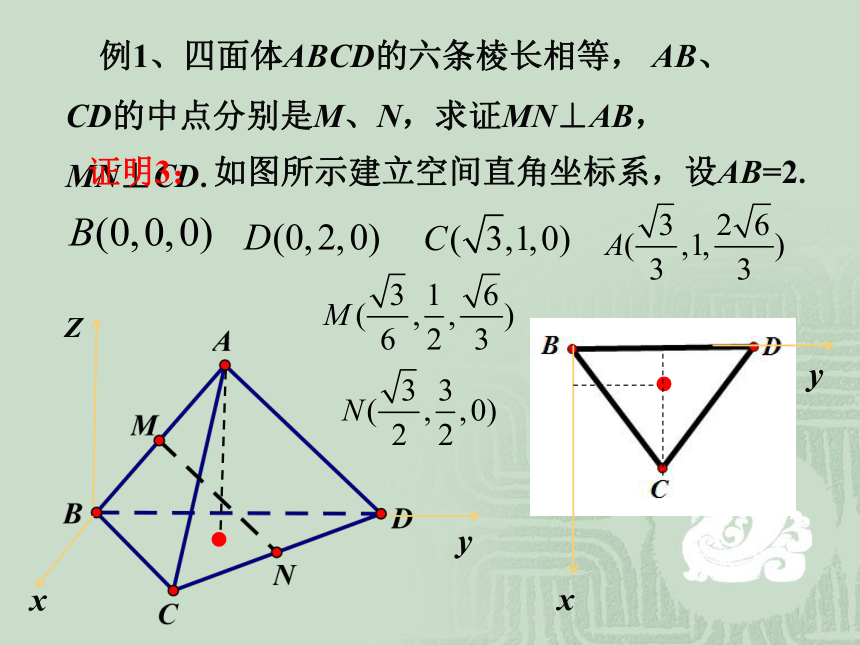
的中点分别是M、N,求证MN⊥AB, MN⊥CD.证明2:MN⊥AB, 同理 MN⊥CD. 例1、四面体ABCD的六条棱长相等, AB、CD的中点分别是M、N,求证MN⊥AB, MN⊥CD.证明3: 如图所示建立空间直角坐标系,设AB=2.xyZxy 练习 棱长为a 的正方体 中,E、F分别是棱AB,OA上的动点,且AF=BE,求证:
Zxy 解:如图所示建立空间
直角坐标系,设AF=BE=b.ABCDPEF 证明1:如图所示建立
空间直角坐标系,设DC=1.ABCDPEF 证明2: 证明:设正方体棱长为1, 为单位正交 基底,建立如图所示坐标系D-xyz,所以 证明2:,E是AA1中点, 例3、 正方体平面C1BD. 证明:E求证:平面EBD设正方体棱长为2, 建立如图所示坐标系平面C1BD的一个法向量是E(0,0,1)D(0,2,0)B(2,0,0)设平面EBD的一个法向量是平面C1BD. 平面EBD 证明2:E,E是AA1中点, 例3、正方体平面C1BD. 求证:平面EBD夹角问题:lmlm夹角问题:ll夹角问题:夹角问题:
的中点分别是M、N,求证MN⊥AB, MN⊥CD. 立几法证明1: 例1、四面体ABCD的六条棱长相等, AB、CD
的中点分别是M、N,求证MN⊥AB, MN⊥CD.证明2:MN⊥AB, 同理 MN⊥CD. 例1、四面体ABCD的六条棱长相等, AB、CD的中点分别是M、N,求证MN⊥AB, MN⊥CD.证明3: 如图所示建立空间直角坐标系,设AB=2.xyZxy 练习 棱长为a 的正方体 中,E、F分别是棱AB,OA上的动点,且AF=BE,求证:
Zxy 解:如图所示建立空间
直角坐标系,设AF=BE=b.ABCDPEF 证明1:如图所示建立
空间直角坐标系,设DC=1.ABCDPEF 证明2: 证明:设正方体棱长为1, 为单位正交 基底,建立如图所示坐标系D-xyz,所以 证明2:,E是AA1中点, 例3、 正方体平面C1BD. 证明:E求证:平面EBD设正方体棱长为2, 建立如图所示坐标系平面C1BD的一个法向量是E(0,0,1)D(0,2,0)B(2,0,0)设平面EBD的一个法向量是平面C1BD. 平面EBD 证明2:E,E是AA1中点, 例3、正方体平面C1BD. 求证:平面EBD夹角问题:lmlm夹角问题:ll夹角问题:夹角问题:
