3.2.3 立体几何中的向量方法 课件3
文档属性
| 名称 | 3.2.3 立体几何中的向量方法 课件3 |  | |
| 格式 | zip | ||
| 文件大小 | 775.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-14 20:32:40 | ||
图片预览








文档简介
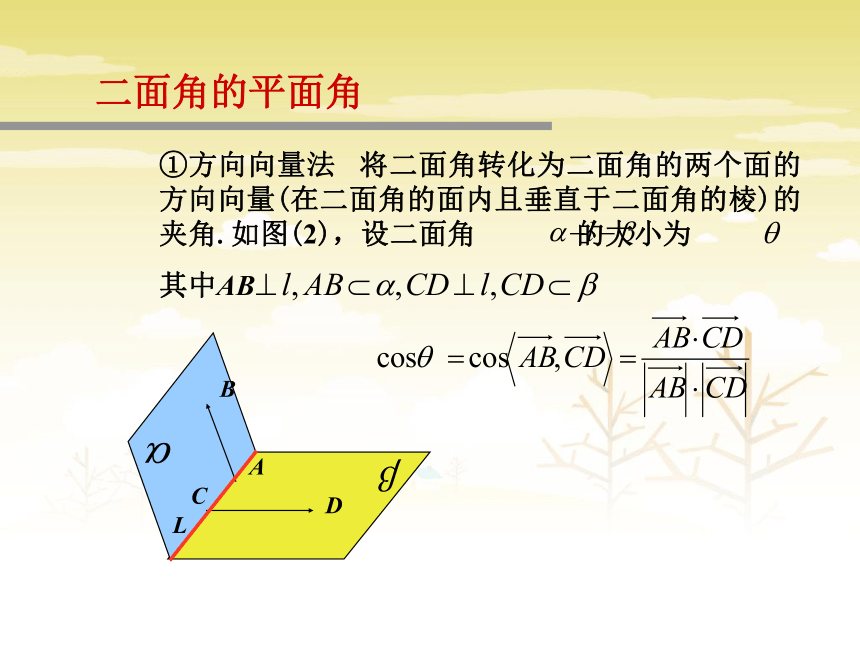
课件23张PPT。3.2.3立体几何中的向量方法空间“角度”问题一、复习引入用空间向量解决立体几何问题的“三步曲”.(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义.(化为向量问题)(进行向量运算)(回到图形)向量的有关知识:两向量数量积的定义:a·b=|a|·|b|·cos〈a,b〉两向量夹角公式:cos 〈a,b〉 =直线的方向向量:与直线平行的非零向量平面的法向量:与平面垂直的向量(课本第107页练习2)如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 二面角的平面角①方向向量法 将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角.如图(2),设二面角 的大小为
其中AB 例1:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 .求库底与水坝所成二面角的余弦值. 解:如图,化为向量问题根据向量的加法法则进行向量运算于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角.因此所以回到图形问题库底与水坝所成二面角的余弦值为 例1:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 .求库底与水坝所成二面角的余弦值. 思考: (1)本题中如果夹角 可以测出,而AB未知,
其他条件不变,可以计算出AB的长吗?分析:∴ 可算出 AB 的长. (2)如果已知一个四棱柱的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间夹角的余弦值吗? 分析:如图,设以顶点 为端点的对角线
长为 ,三条棱长分别为 各棱间夹角为 . (3)如果已知一个四棱柱的各棱长都等于 ,并且以某一顶点为端点的各棱间的夹角都等于 ,那么可以确定这个四棱柱相邻两个夹角的余弦值吗?A1B1C1D1ABCD分析:二面角平面角向量的夹角回归图形 解:如图,在平面 AB1 内过 A1 作
A1E⊥AB 于点 E,EF在平面 AC 内作 CF⊥AB 于 F.∴可以确定这个四棱柱相邻两个夹角的余弦值.空间“夹角”问题1.异面直线所成角lmlm若两直线 所成的角为 , 则例2解:以点C为坐标原点建立空间直角坐标系 如图所示,设 则: 所以:所以 与 所成角的余弦值为练习:在长方体 中,①方向向量法 将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角.如图(2),设二面角 的大小为
其中AB 2、二面角注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角 将二面角转化为二面角的两个面的法向量的夹角.如图,向量 ,
则二面角 的大小 =〈 〉
2、二面角若二面角 的大小为 , 则②法向量法例2 正三棱柱 中,D是AC的中点,当 时,求二面角
的余弦值.故则可设 =1, ,则B(0,1,0)
作 于E, 于F,
则〈 〉即为二面角 的大小
在 中,
即E分有向线段 的比为由于 且 ,所以 在 中,同理可求 ∴即二面角 的余弦值为 解法二:同法一,以C为原点建立空间直角坐标系 C-xyz 在坐标平面yoz中 设面 的一个法向量为 同法一,可求 B(0,1,0)∴由 得解得 所以,可取 即二面角 的余弦值为 方向朝面外, 方向朝面内,属于“一进一出”的情况,二面角等于法向量夹角1. 已知正方体 的边长为2,
O为AC和BD的交点,M为 的中点
(1) 求证: 直线 面MAC
? (2)求二面角 的余弦值
巩固练习2. 线面角2. 线面角l设直线l的方向向量为 ,平面 的法向量为 ,且直线 与平面 所成的角为 ( ),则
其中AB 例1:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 .求库底与水坝所成二面角的余弦值. 解:如图,化为向量问题根据向量的加法法则进行向量运算于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角.因此所以回到图形问题库底与水坝所成二面角的余弦值为 例1:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 .求库底与水坝所成二面角的余弦值. 思考: (1)本题中如果夹角 可以测出,而AB未知,
其他条件不变,可以计算出AB的长吗?分析:∴ 可算出 AB 的长. (2)如果已知一个四棱柱的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间夹角的余弦值吗? 分析:如图,设以顶点 为端点的对角线
长为 ,三条棱长分别为 各棱间夹角为 . (3)如果已知一个四棱柱的各棱长都等于 ,并且以某一顶点为端点的各棱间的夹角都等于 ,那么可以确定这个四棱柱相邻两个夹角的余弦值吗?A1B1C1D1ABCD分析:二面角平面角向量的夹角回归图形 解:如图,在平面 AB1 内过 A1 作
A1E⊥AB 于点 E,EF在平面 AC 内作 CF⊥AB 于 F.∴可以确定这个四棱柱相邻两个夹角的余弦值.空间“夹角”问题1.异面直线所成角lmlm若两直线 所成的角为 , 则例2解:以点C为坐标原点建立空间直角坐标系 如图所示,设 则: 所以:所以 与 所成角的余弦值为练习:在长方体 中,①方向向量法 将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角.如图(2),设二面角 的大小为
其中AB 2、二面角注意法向量的方向:同进同出,二面角等于法向量夹角的补角;一进一出,二面角等于法向量夹角 将二面角转化为二面角的两个面的法向量的夹角.如图,向量 ,
则二面角 的大小 =〈 〉
2、二面角若二面角 的大小为 , 则②法向量法例2 正三棱柱 中,D是AC的中点,当 时,求二面角
的余弦值.故则可设 =1, ,则B(0,1,0)
作 于E, 于F,
则〈 〉即为二面角 的大小
在 中,
即E分有向线段 的比为由于 且 ,所以 在 中,同理可求 ∴即二面角 的余弦值为 解法二:同法一,以C为原点建立空间直角坐标系 C-xyz 在坐标平面yoz中 设面 的一个法向量为 同法一,可求 B(0,1,0)∴由 得解得 所以,可取 即二面角 的余弦值为 方向朝面外, 方向朝面内,属于“一进一出”的情况,二面角等于法向量夹角1. 已知正方体 的边长为2,
O为AC和BD的交点,M为 的中点
(1) 求证: 直线 面MAC
? (2)求二面角 的余弦值
巩固练习2. 线面角2. 线面角l设直线l的方向向量为 ,平面 的法向量为 ,且直线 与平面 所成的角为 ( ),则
